数据结构与算法 -二叉树

二叉树相关算法

1. 二叉树基本知识

（1）二叉树结构

public class Node {
    V value;
    Node left;
    Node right;
}
1
2
3
4
5

left和right只能往下指，没有节点就为空。
（2）创建二叉树
对于一个完全二叉树，父节点为i, 左子节点为2i+1，右子节点为2i+2，当节点index为i时，其父节点index为(i-1)/2。
对于非完全二叉树，我们可以将其看为完全二叉树，没有节点的地方补null。

private static Node createBinaryTree(int[] numbers) {
        Node root = null;
        if (numbers != null && numbers.length > 0) {
            List<Node> nodeList = new ArrayList<>();
            for (int number : numbers) {
                if (number == 0) {
                    nodeList.add(null);
                } else {
                    nodeList.add(new Node(number));
                }
            }
            int tmp = 0;
            while (tmp <= (numbers.length - 2) / 2) {
                if (nodeList.get(tmp) != null) {
                    if (2 * tmp + 1 < numbers.length) {
                        nodeList.get(tmp).left = nodeList.get(2 * tmp + 1);
                    }
                    if (2 * tmp + 2 < numbers.length) {
                        nodeList.get(tmp).right = nodeList.get(2 * tmp + 2);
                    }
                }
                tmp++;
            }
            root = nodeList.get(0);
        }
        return root;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

2. 二叉树遍历

二叉树的先序，中序，后序遍历(指头节点)
先序：任何子树的处理顺序都是，头节点->左子树->右子树
中序：任何子树的处理顺序都是，左子树->头节点->右子树
后序: 任何子树的处理顺序都是，左子树->右子树->头节点
注意：拿子树节点，就需要按照规则，把所有子树的先拿完。

（1）递归序

private static void f(Node root){
        if(root==null){
            return;
        }
        //root第一次出现
        prePass(root.left);
        //root第二次出现
        prePass(root.right);
        //root第三次出现
    }
1
2
3
4
5
6
7
8
9
10

（2）先序遍历
在递归序中先打印头节点的值
① 递归实现

private static void prePass(Node root){
        if(root==null){
            return;
        }
        System.out.println(root.value);
        prePass(root.left);
        prePass(root.right);
    }
1
2
3
4
5
6
7
8

② 非递归实现

因为先序遍历，先打印头节点，再打印左节点，最后打印右节点。我们可以准备一个栈，头节点先进栈，每次弹出头节点之后，打印头节点的值，再将右子节点，左子节点依次放入栈中。然后继续弹出，因为栈具有逆序，所以会先弹出左子节点，再弹出右子节点。

private static void noRecursivePrePass(Node root){
        if(root!=null){
            Stack<Node> nodeStack = new Stack<>();
            nodeStack.add(root);
            while (!nodeStack.empty()){
                Node tmp = nodeStack.pop();
                System.out.print(tmp.value+" ");
                if(tmp.right!=null){
                    nodeStack.add(tmp.right);
                }
                if(tmp.left!=null){
                    nodeStack.add(tmp.left);
                }
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

（3）中序遍历
在左节点之后，打印头节点的值
① 递归实现

private static void midPass(Node root){
        if(root==null){
            return;
        }
        midPass(root.left);
        System.out.println(root.value);
        midPass(root.right);
    }
1
2
3
4
5
6
7
8

② 非递归实现
整条左链压入栈中，若已经没有左子节点，则弹出并打印节点，并将右子节点压入栈中。然后重复上面过程。

private static void noRecursiveMidPass(Node root) {
        if (root != null) {
            Stack<Node> nodeStack = new Stack<>();
            while (!nodeStack.isEmpty() || root != null) {
                if (root != null) {
                    nodeStack.add(root);
                    root = root.left;
                } else {
                    root = nodeStack.pop();
                    System.out.print(root.value);
                    root = root.right;
                }
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

（4）后序遍历
在左右节点之后，打印头节点的值
① 递归实现

private static void postPass(Node root){
        if(root==null){
            return;
        }
        postPass(root.left);
        postPass(root.right);
        System.out.println(root.value);
    }
1
2
3
4
5
6
7
8

② 非递归实现

解法一：
对于先序遍历的非递归实现，我们通过先将头节点压栈并出栈，然后将右子节点压栈，将左子节点压栈，之后再使左子节点出栈，右子节点出栈。从而出现了头左右的排序。若先将左子节点入栈，再将右子节点入栈，就会出现头右左的排序，倒叙为左右头，为后序遍历。因此再准备一个栈，每次节点弹出时，都进入另一个栈中，由于栈先进后出，具有倒叙特点，因此最后出这个栈的结果就是后序遍历结果。

private static void noRecursivePostPass(Node root){
        if(root!=null){
            Stack<Node> nodeStack = new Stack<>();
            Stack<Node> resultStack = new Stack<>();
            Node tmp;
            nodeStack.add(root);
            while (!nodeStack.isEmpty()){
                tmp = nodeStack.pop();
                resultStack.add(tmp);
                if(tmp.left!=null){
                    nodeStack.add(tmp.left);
                }
                if(tmp.right!=null){
                    nodeStack.add(tmp.right);
                }
            }
            while (!resultStack.isEmpty()){
                System.out.print(resultStack.pop().value);
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

解法二：
解法一使用了两个栈，空间占用多。我们可以使用两个Node指针，一个root一直指向栈顶位置，代表需要处理的节点，一个child指向上一次打印的节点，若child指向左子节点，则代表这次应该处理右子节点了，若指向右子节点，则表示左右子节点都已经打印，可以打印父节点了。

private static void noRecursivePostPass(Node root) {
        if (root != null) {
            Stack<Node> nodeStack = new Stack<>();
            nodeStack.push(root);
            Node child;
            while (!nodeStack.empty()) {
                child = nodeStack.peek();
                if (child.left != null && root != child.left && root != child.right) {
                    nodeStack.push(child.left);
                } else if (child.right != null && root != child.right) {
                    nodeStack.push(child.right);
                } else {
                    System.out.print(nodeStack.pop().value + " ");
                    root = child;
                }
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

（5）实现二叉树的层次遍历
本质是宽度优先遍历，用队列
首先将父节点入队列，然后出队列一个节点，并打印此节点，若该节点的左子节点不为空，则将左子节点入队列，若右子节点不为空，则将右子节点入队列。每次都会出队列一个节点并打印。

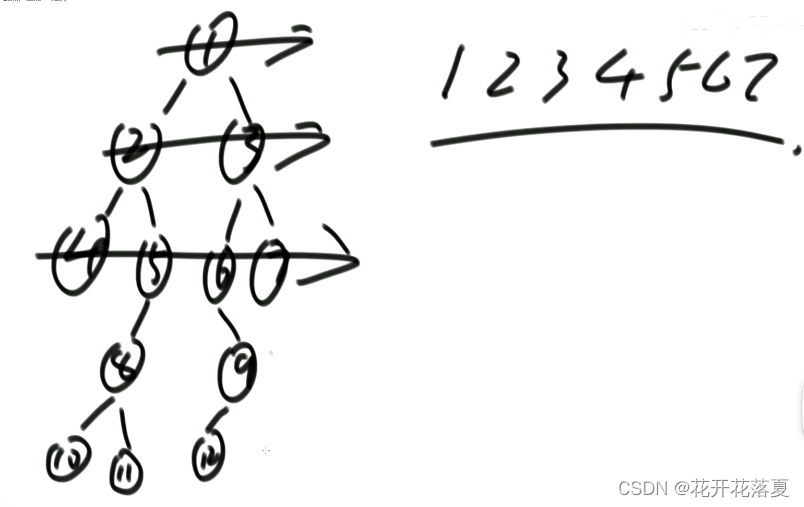
private static void levelPass(Node root) {
        if (root != null) {
            Queue<Node> nodeQueue = new LinkedList<>();
            Node tmp;
            nodeQueue.add(root);
            while (!nodeQueue.isEmpty()) {
                tmp = nodeQueue.poll();
                System.out.print(tmp.value);
                if (tmp.left != null) {
                    nodeQueue.add(tmp.left);
                }
                if (tmp.right != null) {
                    nodeQueue.add(tmp.right);
                }
            }
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

(6) 寻找二叉树最宽的一层
可以通过设置flag变量的方式，来发现某一层的结束。由此可以发现二叉树每层的宽度。
方案一
使用一个map来记录每个节点的层数，这样很容易区分每一层有多少个节点

private static int getMaxWidthOfTree(Node root) {
        int max = 0, currentLevel, level, currentLevelCount = 0;
        Queue<Node> nodeQueue = new LinkedList<>();
        Map<Node, Integer> nodeLevelMap = new HashMap<>();
        Node tmp;
        level = 1;
        nodeLevelMap.put(root, level);
        nodeQueue.add(root);
        while (!nodeQueue.isEmpty()) {
            tmp = nodeQueue.poll();
            currentLevel = nodeLevelMap.get(tmp);
            if (level == currentLevel) {
                currentLevelCount++;
            } else {
                max = Math.max(max, currentLevelCount);
                //The current node is the next level node, so set level to the next level, and set count to 1
                level = currentLevel;
                currentLevelCount = 1;
            }
            if (tmp.left != null) {
                nodeLevelMap.put(tmp.left, currentLevel + 1);
                nodeQueue.add(tmp.left);
            }
            if (tmp.right != null) {
                nodeLevelMap.put(tmp.right, currentLevel + 1);
                nodeQueue.add(tmp.right);
            }
        }
        //We don't compare max and the last level count, so compare the in the below code.
        return Math.max(max, currentLevelCount);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

方案二
使用两个遍历来记录最后的节点，一个记录当前层最后节点，一个记录下一层最后的节点。每次都子节点入队列时，都更新下一次最后一个节点，因此当当前层最后一个节点入队列时，一定能找到下一层最后一个节点。

private static int getMaxWidthOfTree(Node root) {
        int max = 0, curLevelCount = 0;
        Queue<Node> nodeQueue = new LinkedList<>();
        Node curEnd = root, nextEnd = null, tmp;
        nodeQueue.add(root);
        while (!nodeQueue.isEmpty()) {
            tmp = nodeQueue.poll();
            curLevelCount++;
            if (tmp.left != null) {
                nextEnd = tmp.left;
                nodeQueue.add(tmp.left);
            }
            if (tmp.right != null) {
                nextEnd = tmp.right;
                nodeQueue.add(tmp.right);
            }
            if (tmp == curEnd) {
                max = Math.max(max, curLevelCount);
                curEnd = nextEnd;
                curLevelCount = 0;
            }
        }
        return max;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

(7) 二叉树的序列化和反序列化
可以用先序或者中序或者后序或者层次遍历，来实现二叉树的序列化，用了什么方式序列化，就用什么样的方式反序列化。
注意：为了记录二叉树的结构，不要忽略空节点，用null补全。

例1：使用先序遍历序列化
注意：先序，中序，后序遍历都是类似操作

private static Queue<Node> serializeBinaryTree(Node root) {
        Queue<Node> nodeQueue = new LinkedList<>();
        prePass(root, nodeQueue);
        return nodeQueue;
    }

    private static void prePass(Node root, Queue<Node> nodeQueue) {
        if (root == null) {
            nodeQueue.add(null);
            return;
        }
        nodeQueue.add(root);
        prePass(root.left, nodeQueue);
        prePass(root.right, nodeQueue);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

使用先序遍历反序列化

private static Node deSerializeBinaryTree(Queue<Node> nodeQueue) {
        Node node = nodeQueue.poll();
        if (node == null) {
            return null;
        } else {
            node.left = deSerializeBinaryTree(nodeQueue);
            node.right = deSerializeBinaryTree(nodeQueue);
        }
        return node;
    }
1
2
3
4
5
6
7
8
9
10

例2：使用层次遍历实现序列化

序列化：先层次遍历二叉树，将节点及其子节点加入队列中，若子节点为null，就把null也加入队列中

private static Queue<Node> serializeBinaryTree(Node root) {
        Queue<Node> nodeQueue = new LinkedList<>();
        Queue<Node> tmp = new LinkedList<>();
        Node node;
        tmp.add(root);
        while (!tmp.isEmpty()){
            node=tmp.poll();
            nodeQueue.add(node);
            if(node!=null){
                tmp.add(node.left);
                tmp.add(node.right);
            }
        }
        return nodeQueue;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

反序列化：先遍历节点队列，取出一个节点，若节点不为null，则说明该节点有左右子节点，因此再取出该节点的左右子节点。使用一个队列tmp记录有子节点的节点，因此若左右子节点不为空，则加入到tmp中。

private static Node deSerializeBinaryTree(Queue<Node> nodeQueue) {
        Node root = nodeQueue.poll();
        if (root != null) {
            Queue<Node> tmp = new LinkedList<>();
            Node node;
            tmp.add(root);
            while (!tmp.isEmpty()) {
                node = tmp.poll();
                node.left = nodeQueue.poll();
                node.right = nodeQueue.poll();
                if (node.left != null) {
                    tmp.add(node.left);
                }
                if (node.right != null) {
                    tmp.add(node.right);
                }
            }
        }
        return root;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

3. 二叉树的递归套路

可以解决面试中绝大多数的二叉树问题，尤其是树型dp问题，本质是利用递归遍历二叉树的便利性
流程如下：
（1）假设以X节点为头，假设可以向X左树和X右树要任何信息
（2）在上一步的假设下，讨论以X为头节点的树，得到答案的可能性
（3）列出所有可能性后，确定到底需要向左树和右树要什么样的信息
（4）把左树信息和右树信息求全集，就是任何一棵子树都需要返回的信息S
（5）递归函数都返回S，每一棵子树都这么要求
（6）写代码，在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息

1. 如何设计一个打印整棵树的打印函数

注意打印整棵树，需要保持树的结构
（1）将整棵树填补成一个完全二叉树再打印

这种方法消耗太大，推荐采用第二种方法。
（2）倒着打印，不用补树

注意：可以将树逆时针旋转90度，当我们进行先右，再中，再左的遍历时，刚好可以使得节点按行打印。每个节点占一行。

//Because the diff value has diff length, so we set the length of value to length.
    //If the length of "tagvaluetag" is shorter, we use " " to fill the space
    //Use height to record the location of node,height is bigger, the location is far from begin of a line.
    private static void inOrder(Node root, String tag, int height, int length) {
        if (root == null) {
            return;
        }
        inOrder(root.right, "r", height + 1, length);
        String value = tag + root.value + tag;
        int leftLength = (length - value.length()) / 2;
        int rightLength = length - leftLength - value.length();
        value = getSpace(leftLength) + value + getSpace(rightLength);
        System.out.println(getSpace(height * length) + value);
        inOrder(root.left, "l", height + 1, length);
    }

    private static String getSpace(int length) {
        return " ".repeat(Math.max(0, length));
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

2. 求二叉树某个节点的后继节点

二叉树结构如下定义：

public class Node {
    int value;
    Node left;
    Node right;
    Node parent;
}
1
2
3
4
5
6

给你二叉树中的某个节点，返回该节点中序遍历的后续节点
注意：后继节点指，一个节点在其中序遍历的顺序中，下一个节点为后继节点。

题解：
对于一个节点，有以下三种情况：
（1）其有右子树，则后继节点为右子树的最左节点
（2）其没有右子树，但往上追溯，此节点或某个父节点为A节点的左子节点，则后继节点为A节点
（3）其没有右子树，且往上追溯，此节点或某个父节点没有父节点为左子节点，则为最右的节点，无后续节点。

public Node getTheNextNode(Node targetNode) {
        Node nextNode = null;
        if (targetNode == null) {
            return targetNode;
        } else {
        	//targetNode is the parent node, the next node of it is the most left node.
            if (targetNode.right != null) {
                nextNode = targetNode.right;
                while (nextNode.left != null) {
                    nextNode = nextNode.left;
                }
            } else {
            	//If the targetNode is the left child node, the next node is it's parent.
                Node parent = targetNode.parent;
                //In the while condition, the targetNode is the right node
                while (parent != null && parent.left != targetNode) {
                    targetNode = parent;
                    parent = targetNode.parent;
                }
                nextNode = parent;
            }
            return nextNode;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

3. 判断一棵树是否为平衡二叉树

平衡二叉树：该树中的每一颗树，左右子树的高度差都不超过1
每一颗子树都是平衡树
判断一棵树是否为平衡二叉树，我们需要：
1.知道该树的左右子树是不是平衡二叉树，若有一个不是，则该树也不可能是
2.知道该树的左右子树的高度，从而根据高度判断该树是不是平衡二叉树
因此需要从子树知道下面的信息

public class Info {
    int height;
    boolean isBalance;

    public Info(int height, boolean isBalance) {
        this.height = height;
        this.isBalance = isBalance;
    }

    public int getHeight() {
        return height;
    }

    public void setHeight(int height) {
        this.height = height;
    }

    public boolean isBalance() {
        return isBalance;
    }

    public void setBalance(boolean balance) {
        isBalance = balance;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

使用递归从子树获得信息：

private static Info getInfoOfTree(Node root) {
        if (root == null) {
            return new Info(0, true);
        } else {
            Info leftInfo = getInfoOfTree(root.left);
            Info rightInfo = getInfoOfTree(root.right);
            int height = Math.max(leftInfo.getHeight(), rightInfo.getHeight()) + 1;
            boolean isBalance = false;
            if (leftInfo.isBalance && rightInfo.isBalance && Math.abs(rightInfo.height - leftInfo.height) < 2) {
                isBalance = true;
            }
            root.info = new Info(height, isBalance);
            return root.info;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

4. 求二叉树的最大距离

给定一棵二叉树的头节点head，任何两个节点之间都存在距离，返回整棵二叉树的最大距离。
节点之间的距离指从一个节点到另一个节点的最精简距离

对于一个根节点为X的二叉树，最大距离有两种可能：
（1）最大距离和根节点无关
此时的最大距离为左树的最大距离或者右树的最大距离

（2）最大距离与根节点有关，即通过根节点
左树离根节点最远的点到右树离根节点最远的点，即左高+1+右高

二叉树递归就是跟左树和右树要信息，因为需要最大距离和树的高度，因此向左树和右树要最大距离和树的高度。对于任何一个节点，由于不知道它的最大距离与此节点是否有关系，因此需要同时求(1)(2)两种情况，并取最大的值作为最大距离。此外，在求最大距离时，由于要综合左右子树的情况，因此采用后序遍历。

package test;

public class Info {
    int height;
    int maxInstance;

    public Info(int height, int maxInstance) {
        this.height = height;
        this.maxInstance = maxInstance;
    }

    public int getHeight() {
        return height;
    }
    

    public int getMaxInstance() {
        return maxInstance;
    }
}

private static Info getMaxInstance(Node node) {
        if (node == null) {
            return new Info(0, 0);
        }

        Info leftInfo = getMaxInstance(node.left);
        Info rightInfo = getMaxInstance(node.right);

        int height = Math.max(leftInfo.height, rightInfo.height) + 1;
        int instance = Math.max(Math.max(leftInfo.maxInstance, rightInfo.maxInstance), leftInfo.height + 1 + rightInfo.height);
        return new Info(height, instance);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

5. 求派对的最大快乐值

员工信息定义如下：

class Employee{
        public int happy;//这名员工可以带来的快乐值
        List<Employee> subOrdinates;//这名员工的直属下级
    }
1
2
3
4

公司的每个员工都符合Employee类的描述。整个公司的人员结构可以看作是一棵标准的，没有环的多叉树。树的头节点是公司的唯一老板。除老板之外的每个员工都有唯一的直接上级。叶节点是没有任何下属的基层员工(subOrdinates列表为空)，除基层员工外，每个员工都有一个或多个直接下级。

这个公司现在要办party，你可以绝对哪些员工来，哪些员工不来，规则：
1.如果某个员工来了，那这个员工的所有直接下级都不能来。
2.排队的整体快乐值是到场所有快乐值的累加
3.你的目标是让排队的整体快乐值尽量大。
给定一棵多叉树的头节点boss，请返回排队的最大快乐值

分析：对于一个下图所示的节点，有两种可能。
第一种X来，快乐值 = x的快乐值+a不来情况下a子树的最大值+b不来情况下b子树的最大值+c不来情况下c子树的最大快乐值
第二种X不来，X不来，不一定代表着a,b,c必须来，要看实际情况，哪个快乐值大选哪个。快乐值 = 0 + max{a来, a不来} + max{b来, b不来} + max{c来, c不来}

public class Node {
    public int happy;//这名员工可以带来的快乐值
    List<Node> subOrdinates;//这名员工的直属下级

    public Node(int happy, List<Node> subOrdinates) {
        this.happy = happy;
        this.subOrdinates = subOrdinates;
    }
}

private static Info mostHappyValue(Node node) {
        if (node == null) {
            return new Info(0, 0);
        }
        int comeHappy = node.happy;
        int notComeHappy = 0;
        List<Node> subOrdinates = node.subOrdinates;
        for (Node subNode : subOrdinates) {
            Info info = mostHappyValue(subNode);
            comeHappy += info.notComeHappy;
            notComeHappy += Math.max(info.comeHappy, info.notComeHappy);
        }
        return new Info(comeHappy, notComeHappy);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24