-
Making better mistakes -- Mistake severity issues
Contents
- [CVPR 2020] Making better mistakes: Leveraging class hierarchies with deep networks
- [BMVC 2021] Leveraging Class Hierarchies with Metric-Guided Prototype Learning
- [ICLR 2021] No cost likelihood manipulation at test time for making better mistakes in deep networks
- [ECCV 2022] Learning Hierarchy Aware Features for Reducing Mistake Severity
[CVPR 2020] Making better mistakes: Leveraging class hierarchies with deep networks
- Bertinetto, Luca, et al. “Making better mistakes: Leveraging class hierarchies with deep networks.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.
- code: https://github.com/fiveai/making-better-mistakes
Introduction
- Mistake severity issue 是指在对样本分类时,不同误分类情况的严重程度应该是不同的,例如将橘子误识别为橙子和将橘子误识别为橘猫的严重程度应该是不同的,又比如在自动驾驶中将路灯误识别为树和将行人误识别为树的严重程度也应该是不同的,后者会进一步影响自动驾驶后续的决策和规划。但在使用 CE 训练时,模型对不同的误分类情况是一视同仁的, i.e. “flat” (i.e. hierarchy-agnostic) classifiers。如下图所示,尽管近年来模型的错误率有了极大的提升,但 Mistake severity issue 并未得到改善 (Here, a
m
i
s
t
a
k
e
mistake
mistake is defined as a top-1 prediction which differs from the ground-truth class, and the
s
e
v
e
r
i
t
y
severity
severity of such a mistake is the height of the lowest common ancestor of the predicted and ground-truth classes in the hierarchy)
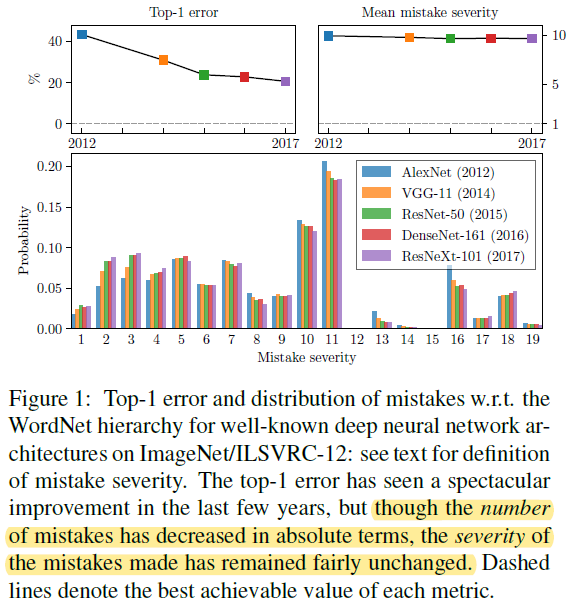 (Introduction 第二段感觉写得不错,主要讲述了 CV 领域利用 taxonomic hierarchy tree 提升模型性能的历史,包括它的重要性以及当前被忽略的原因)
(Introduction 第二段感觉写得不错,主要讲述了 CV 领域利用 taxonomic hierarchy tree 提升模型性能的历史,包括它的重要性以及当前被忽略的原因) - 为了解决上述问题,作者基于 taxonomic hierarchy tree 提出了两种 CE 的改进损失函数来学得 hierarchy-informed classifiers
Method
Framework and related work
- 如下为标准的分类损失,其中
y
(
C
i
)
y(C_i)
y(Ci) 为 label embed (e.g. one-hot vector)
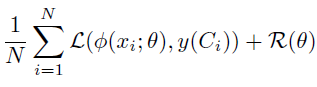
为了将 class relationships H \mathcal H H 引入损失函数,作者总结了当前主流的三种方法以及相关工作,并分别提出了一种新的 Hierarchical loss 和 Label-embedding method:
- (1) Label-embedding methods y H ( C ) y^{\mathcal H}(C) yH(C): 将 class representation y ( C ) y(C) y(C) 替换为 y H ( C ) y^{\mathcal H}(C) yH(C),然后基于标签层次关系或其他信息,在这些 embedded vectors 上施加损失函数使得标签向量的相对位置代表标签的语义关系 (有趣的是,知识蒸馏也可以看作是其中的一种方法,其中 label embed 由 teacher 提供)
- (2) Hierarchical losses L H \mathcal L^{\mathcal H} LH: a higher penalty is assigned to the prediction of a more distant relative of the true label
- (3) Hierarchical architectures ϕ H \phi^{\mathcal H} ϕH: incorporate class hierarchy into the classifier architecture (“divide and conquer”)
Hierarchical cross-entropy (HXE)
- 在层次多标签分类中,样本属于叶节点类别
C
C
C 的概率可以按照条件概率写为如下形式:
p ( C ) = p ( C ( 0 ) , . . . , C ( h ) ) = ∏ l = 0 h − 1 p ( C ( l ) ∣ C ( l + 1 ) ) p(C)=p(C^{(0)},...,C^{(h)})=\prod_{l=0}^{h-1} p\left(C^{(l)} \mid C^{(l+1)}\right) p(C)=p(C(0),...,C(h))=l=0∏h−1p(C(l)∣C(l+1))其中 C ( l + 1 ) C^{(l+1)} C(l+1) 为 C l C^{l} Cl 的父类别, C ( 0 ) = C C^{(0)}=C C(0)=C, C ( h ) = R C^{(h)}=R C(h)=R (根节点), P ( C ( h ) ) = 1 P(C^{(h)})=1 P(C(h))=1 - 根据上式可以将交叉熵损失
−
log
p
(
C
)
-\log p(C)
−logp(C) 写为 hierarchical cross-entropy (HXE)
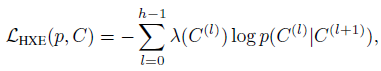 其中
λ
(
C
(
l
)
)
=
exp
(
−
α
h
(
C
)
)
\lambda(C^{(l)})= \exp(−αh(C))
λ(C(l))=exp(−αh(C)) 为层次标签树上
C
(
l
+
1
)
→
C
(
l
)
C^{(l+1)}\rightarrow C^{(l)}
C(l+1)→C(l) 的权重,
h
(
C
)
h(C)
h(C) 为
C
C
C 的高度 (根节点高度最低),因此
α
>
0
\alpha>0
α>0 越大,“generic” information 相对于 “fine-grained” information 就越重要,模型也就越倾向于 “make better mistakes” (不过是以牺牲一定的准确率为代价的)。条件概率可由下式得到
其中
λ
(
C
(
l
)
)
=
exp
(
−
α
h
(
C
)
)
\lambda(C^{(l)})= \exp(−αh(C))
λ(C(l))=exp(−αh(C)) 为层次标签树上
C
(
l
+
1
)
→
C
(
l
)
C^{(l+1)}\rightarrow C^{(l)}
C(l+1)→C(l) 的权重,
h
(
C
)
h(C)
h(C) 为
C
C
C 的高度 (根节点高度最低),因此
α
>
0
\alpha>0
α>0 越大,“generic” information 相对于 “fine-grained” information 就越重要,模型也就越倾向于 “make better mistakes” (不过是以牺牲一定的准确率为代价的)。条件概率可由下式得到
p ( C ( l ) ∣ C ( l + 1 ) ) = p ( C ( l ) ) p ( C ( l + 1 ) ) = ∑ A ∈ Leaves ( C ( l ) ) p ( A ) ∑ B ∈ Leaves ( C ( l + 1 ) ) p ( B ) p\left(C^{(l)} \mid C^{(l+1)}\right)=\frac{p\left(C^{(l)} \right)}{p\left(C^{(l+1)} \right)}=\frac{\sum_{A \in \operatorname{Leaves}\left(C^{(l)}\right)} p(A)}{\sum_{B \in \operatorname{Leaves}\left(C^{(l+1)}\right)} p(B)} p(C(l)∣C(l+1))=p(C(l+1))p(C(l))=∑B∈Leaves(C(l+1))p(B)∑A∈Leaves(C(l))p(A)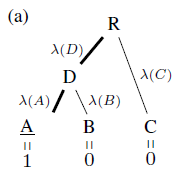
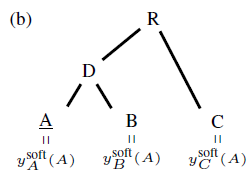
Soft labels
- 在标准交叉熵损失中,label embed 为 one-hot 向量,这里作者根据标签层次关系生成软标签来融入层次标签信息
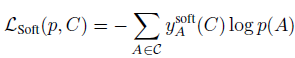 其中,
y
A
s
o
f
t
(
C
)
y_A^{soft}(C)
yAsoft(C) 表示类别
A
A
A 和类别
C
C
C 的相关程度,两个类别越接近,
y
A
s
o
f
t
(
C
)
y_A^{soft}(C)
yAsoft(C) 越大
其中,
y
A
s
o
f
t
(
C
)
y_A^{soft}(C)
yAsoft(C) 表示类别
A
A
A 和类别
C
C
C 的相关程度,两个类别越接近,
y
A
s
o
f
t
(
C
)
y_A^{soft}(C)
yAsoft(C) 越大
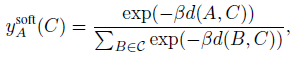 其中,
d
(
A
,
C
)
d(A,C)
d(A,C) 为类别
A
,
C
A,C
A,C 间的距离 (两个类别的最低公共父类别的高度除以树高),
β
>
0
\beta>0
β>0 很大时,软标签与 one-hot label 近似,
β
>
0
\beta>0
β>0 很小时,软标签和均匀分布近似 (Between these extremes, greater probability mass is assigned to classes more closely related to the ground truth, with the magnitude of the difference controlled by
β
β
β.). 这种处理方式的效果应该和用 logit 进行知识蒸馏相类似,在知识蒸馏中软标签是 teacher 提供的,但在这里,软标签是由层次标签提供的
其中,
d
(
A
,
C
)
d(A,C)
d(A,C) 为类别
A
,
C
A,C
A,C 间的距离 (两个类别的最低公共父类别的高度除以树高),
β
>
0
\beta>0
β>0 很大时,软标签与 one-hot label 近似,
β
>
0
\beta>0
β>0 很小时,软标签和均匀分布近似 (Between these extremes, greater probability mass is assigned to classes more closely related to the ground truth, with the magnitude of the difference controlled by
β
β
β.). 这种处理方式的效果应该和用 logit 进行知识蒸馏相类似,在知识蒸馏中软标签是 teacher 提供的,但在这里,软标签是由层次标签提供的
Evaluation
Metrics - Hierarchical measures
- The hierarchical distance of a mistake is the height of the lowest common ancestor (LCA) between the ground truth and the predicted class when the input is misclassified. Hence, it measures the severity of misclassification when only a single class can be considered as a prediction. (Note that LCA is a log-scaled distance: an increment of 1.0 signifies an error of an entire level of the tree. In the simple case of a full binary tree, an increase by one level implies that the number of possible leaf nodes doubles.)
- Warning: 如 Karthik, Shyamgopal, et al. 所述,这一指标存在 bug. 如果想要在这一指标上表现很好,只需要 “make additional low-severity mistakes” 即可,因此不能单看这一个指标,而是要结合 Top-1 Acc 一起分析
- The average hierarchical distance of top- k k k, instead, takes the mean LCA height between the ground truth and each of the k k k most likely classes. This measure can be important when multiple hypotheses of a classifier can be considered for a certain downstream task. (相比 Top-1 Acc,Avg. hier. dist. @1 还考虑了错误分类样本的错误严重程度,在作者的实验中可以看到这两个指标总体上是正相关的)
Experimental results
t i e r e d I m a g e N e t tieredImageNet tieredImageNet- H H H (Word-Net hierarchy of nouns) 和 i N a t u r a l i s t iNaturalist iNaturalist- H H H (biological taxonomy) 都是作者基于 ImageNet 和 iNaturalist19 重新构造的数据集
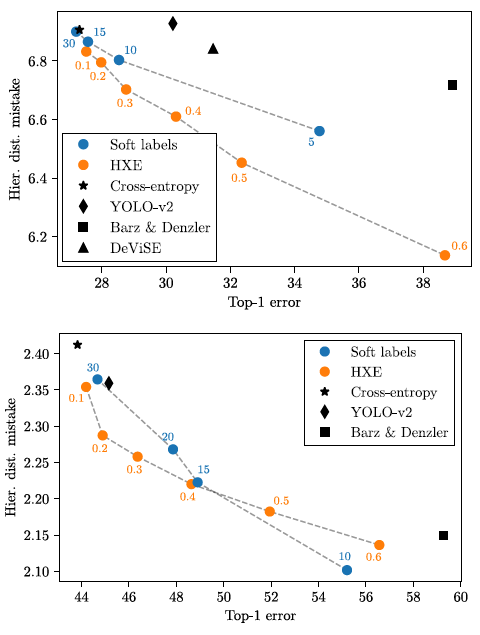
- Top-1 error vs. hierarchical distance of mistakes, for
t
i
e
r
e
d
I
m
a
g
e
N
e
t
tieredImageNet
tieredImageNet-
H
H
H (top) and
i
N
a
t
u
r
a
l
i
s
t
iNaturalist
iNaturalist-
H
H
H (bottom).
- Top-1 error vs. average hierarchical distance of top-
k
k
k (with
k
∈
{
1
,
5
,
20
}
k ∈ \{1, 5, 20\}
k∈{1,5,20}) for
t
i
e
r
e
d
I
m
a
g
e
N
e
t
−
H
tieredImageNet-H
tieredImageNet−H (top three) and
i
N
a
t
u
r
a
l
i
s
t
−
H
iNaturalist-H
iNaturalist−H (bottom three).
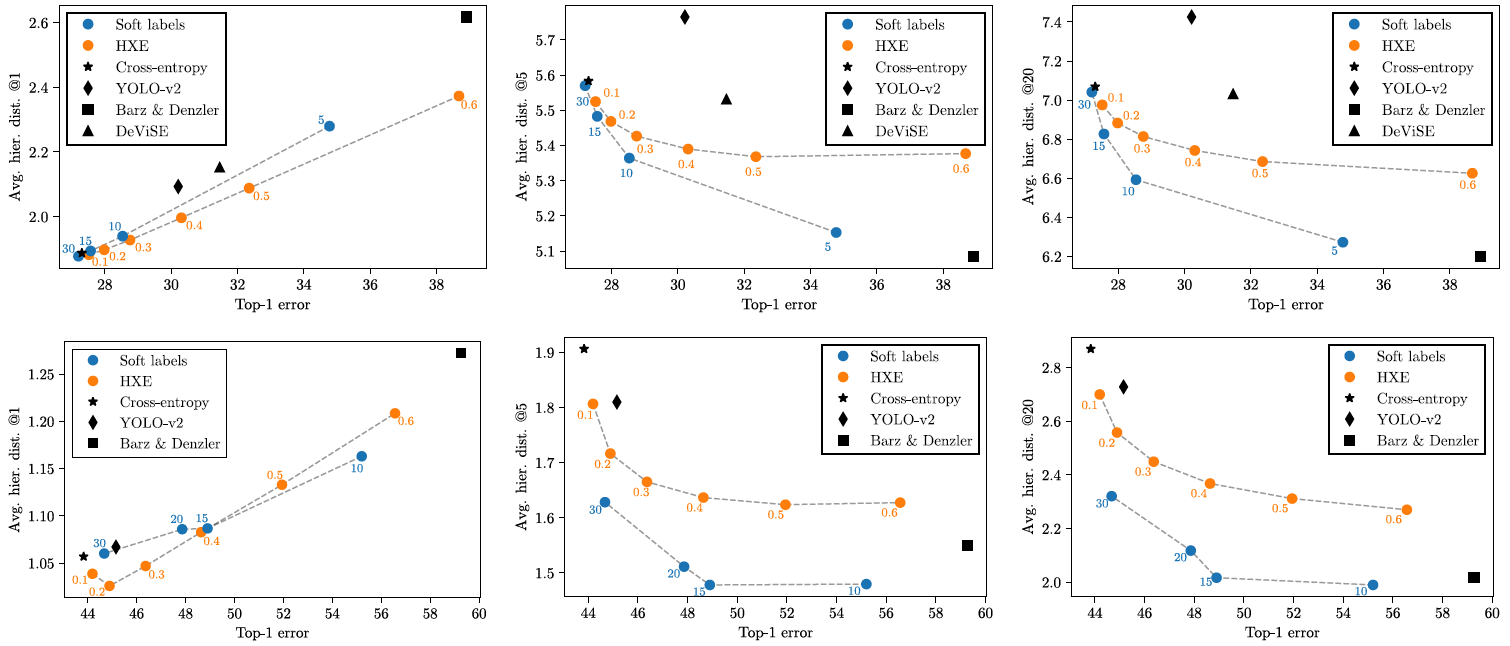 可以看到,Avg. hier. dist. @1 和 Top-1 error 总体上是正相关的 (当准确率很高时,Top-1 预测的类别基本都是正确的,此时 Avg. hier. dist. 也会很小),但 Avg. hier. dist. @
k
k
k (
k
>
1
k>1
k>1) 和 Top-1 error 总体上是负相关的,也就是说,大多数情况下,Making better mistakes 和更高的准确率在一定程度上是冲突的,make better mistakes 能让 Top-
k
k
k 预测里和目标类别相近的类别变多,但却会降低 Top-1 Acc. 作者提出的方法能通过调节超参更好地进行 trade-off,从而在尽量不损失 Top-1 Acc 的情况下降低 Avg. hier. dist. @
k
k
k
可以看到,Avg. hier. dist. @1 和 Top-1 error 总体上是正相关的 (当准确率很高时,Top-1 预测的类别基本都是正确的,此时 Avg. hier. dist. 也会很小),但 Avg. hier. dist. @
k
k
k (
k
>
1
k>1
k>1) 和 Top-1 error 总体上是负相关的,也就是说,大多数情况下,Making better mistakes 和更高的准确率在一定程度上是冲突的,make better mistakes 能让 Top-
k
k
k 预测里和目标类别相近的类别变多,但却会降低 Top-1 Acc. 作者提出的方法能通过调节超参更好地进行 trade-off,从而在尽量不损失 Top-1 Acc 的情况下降低 Avg. hier. dist. @
k
k
k - 基于上述实验,作者为两种方法各选取了两组超参,分别对应 high-distance/low-top1-error (small
α
\alpha
α, large
β
\beta
β) 以及 low-distance/high-top1-error regime (large
α
\alpha
α, small
β
\beta
β)
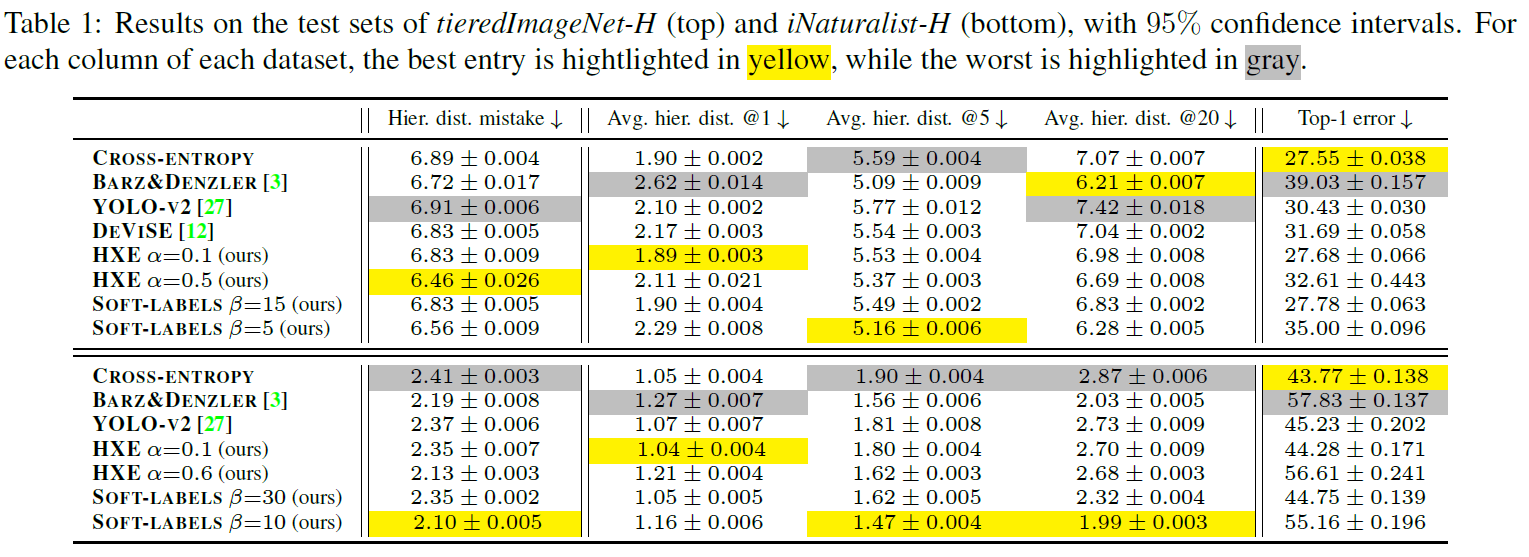
[BMVC 2021] Leveraging Class Hierarchies with Metric-Guided Prototype Learning
- Landrieu, Loic, and Vivien Sainte Fare Garnot. “Leveraging Class Hierarchies with Metric-Guided Prototype Learning.” British Machine Vision Conference (BMVC). 2021.
- code: https://github.com/VSainteuf/metric-guided-prototypes-pytorch
Introduction
- 针对层次多标签分类任务,作者提出 Distortion-Based Penalization 来让类别对应的 prototypes 间的距离和类别节点在层次标签树上的最短距离保持一致,从而提高模型的分类性能
Method
Prototypical Networks
- Prototypical network ( f , π ) (f,\pi) (f,π) 包括用于将样本映射为 embed 的 embedding function f : X → Ω f:\mathcal X\rightarrow\Omega f:X→Ω 和 K K K 个类别的 prototypes 集合 π ∈ Ω K \pi\in\Omega^{K} π∈ΩK,其中 π \pi π 满足属于类别 k k k 的样本 x n x_n xn 对应的 embed f ( x n ) f(x_n) f(xn) 接近 π k \pi_k πk 而远离其他 prototypes
- 样本
x
n
x_n
xn 的类别
z
n
z_n
zn 为
k
k
k 的后验概率即为
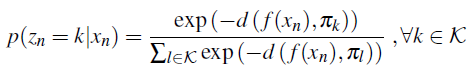 其中
d
d
d 为 embed 之间的距离。分类损失为真实类别的负对数似然:
其中
d
d
d 为 embed 之间的距离。分类损失为真实类别的负对数似然:
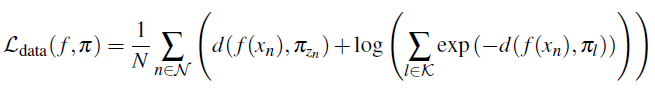
Metric-Guided Penalization
- 对于层次多标签数据集,可以定义 cost matrix D D D,其中 D [ m , n ] D[m,n] D[m,n] 表示类别 m , n m,n m,n 对应节点在类别层次树上的最短路径长度。我们想要 prototypes 间的距离与 cost matrix 保持一致
- Metric Distortion. 现在我们有两个 metric space,分别是类别层次树上定义的 finite metric space
(
K
,
D
)
(\mathcal K,D)
(K,D) 和 embed 空间上定义的 continuous metric space
(
Ω
,
d
)
(\Omega,d)
(Ω,d). 两个 metric space 之间元素映射
k
→
π
k
k\rightarrow\pi_k
k→πk 的 distortion 可以被定义为源空间和目标空间之间的 average relative difference between distances
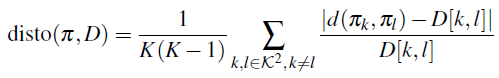 我们想要上述 distortion 尽量小
我们想要上述 distortion 尽量小 - Scale-Free Distortion. 最小化上述 Metric Distortion 会使得 prototypes 间的距离与类别层次树上标签节点间的距离接近,这反而极大地约束了 prototypes 在 embed 空间里的分布 (This imposes a specific scale on the distances between prototypes in the embedding space.),也可能会不利于样本 embed 尽可能远离无关类别的 prototypes. 为了解决上述问题,作者引入了 scalar factor
s
s
s 来计算 Scale-Free Distortion,这样 propotypes 间的距离只需相对得和类别层次树上标签节点间的距离一致即可,不需要保持完全一致
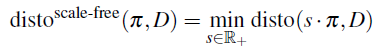
- Distortion-Based Penalization. a smooth surrogate of
disto
scale-free
\text{disto}^{\text{scale-free}}
distoscale-free
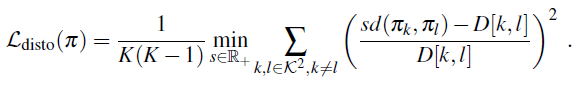 设
α
k
,
l
=
d
(
π
k
,
π
l
)
/
D
[
k
,
l
]
\alpha_{k,l}=d(\pi_k,\pi_l)/D[k,l]
αk,l=d(πk,πl)/D[k,l],令上式对
s
s
s 的偏导为 0 可得
设
α
k
,
l
=
d
(
π
k
,
π
l
)
/
D
[
k
,
l
]
\alpha_{k,l}=d(\pi_k,\pi_l)/D[k,l]
αk,l=d(πk,πl)/D[k,l],令上式对
s
s
s 的偏导为 0 可得
s ∗ = ∑ k , l , k ≠ l α i / ∑ k , l , k ≠ l α i 2 s^*=\sum_{k,l,k\neq l}\alpha_i/\sum_{k,l,k\neq l}\alpha_i^2 s∗=k,l,k=l∑αi/k,l,k=l∑αi2 - Total loss
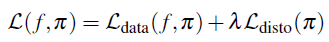
Experiments
- Datasets and Backbones. ResNet-18 for CIFAR100 and iNat-19, FuseNet for NYUDv2, PSE+TAE for S2-Ag
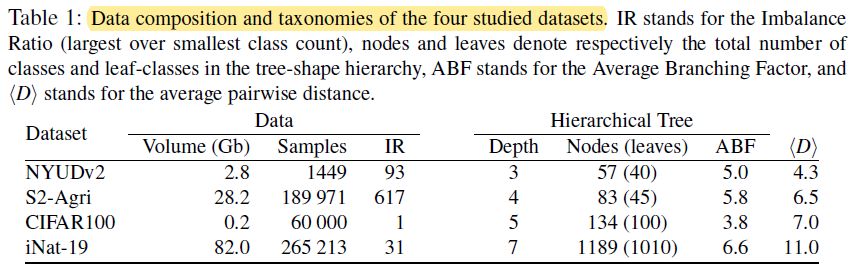
- Competing methods.
- Hierarchical Cross-Entropy (HXE), Soft Labels. Making better mistakes: Leveraging class hierarchies with deep networks.
- Earth Mover Distance regularization (XE+EMD). Squared earth mover’s distance-based loss for training deep neural networks. Account for the relationships between classes with a regularization based on the squared earth mover distance. We use D D D as the ground distance matrix between the probabilistic prediction p p p and the true class y y y.
- Hierarchical Inference (YOLO). YOLO9000: better, faster, stronger. First, the conditional probability that a sample belongs to a class given its parent class is obtained with a soft-max restricted to the class’ co-hyponyms (i.e. siblings). Then, the posterior probability of a leaf class is given by the product of the conditional probability of its ancestors. The loss is defined as the cross-entropy of the resulting probability of the leaf-classes.
- Hyperspherical Prototypes (Hyperspherical-proto). Hyperspherical prototype networks. They advocate to first position prototypes on the hypersphere using a rank-based loss combined with a prototype-separating term. They then use the squared cosine distance between the image embeddings and prototypes to train the embedding network.
- Deep Mean Classifiers (Deep-NCM). DeepNCM: deep nearest class mean classifiers. The prototypes are the cumulative mean of the embeddings of the classes’ samples, updated at each iteration. The embedding network is supervised with L d a t a \mathcal L_{data} Ldata with d d d defined as the squared Euclidean norm.
- Simple prototype learning (Learnt-proto) by setting λ = 0 λ = 0 λ=0. Robust classification with convolutional prototype learning.
- Average Hierarchical Cost (AHC)
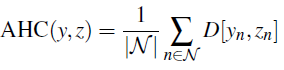 其中
y
n
,
z
n
y_n,z_n
yn,zn 分别为样本
n
n
n 的预测标签和真实标签
其中
y
n
,
z
n
y_n,z_n
yn,zn 分别为样本
n
n
n 的预测标签和真实标签 - Overall Performance
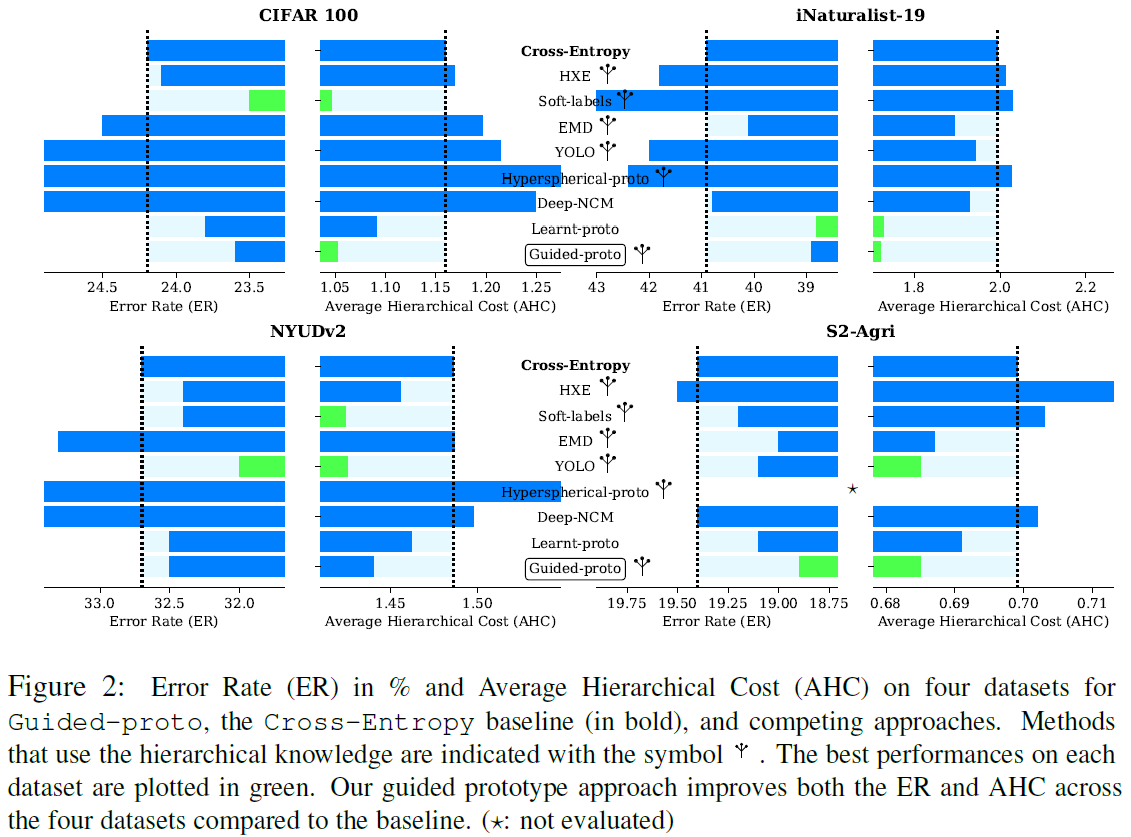
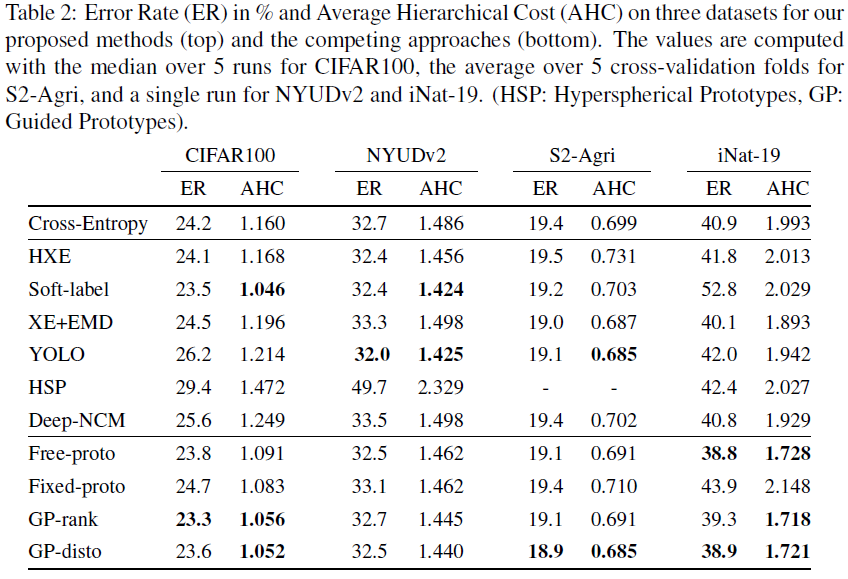
- Ablation Study. (1) 下表中 Fixed-scale 是指先学得 prototypes,然后在模型训练时使用固定的 prototypes;Rank-based guiding 是指用 Hyperspherical prototype networks. 中的排序损失替代 distortion loss,排序损失只要求 prototypes 间的距离排序和类别层次树的节点距离排序一致;Squared Norm 是指用 squared Euclidean norm 替代 Euclidean norm
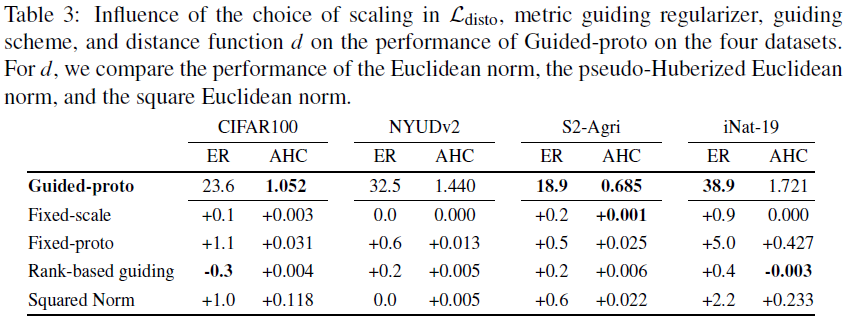 (2) 下面的实验证明模型对
λ
\lambda
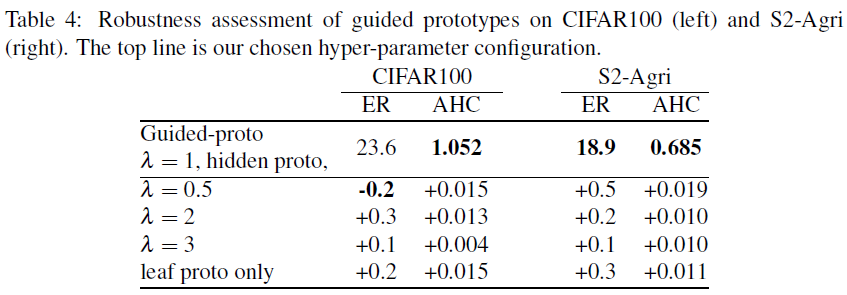
λ 不是特别敏感,并且在 Distortion-Based Penalization 中添加所有类别 (包括叶结点类别的父类) 的约束有助于提高模型性能
(2) 下面的实验证明模型对
λ
\lambda
λ 不是特别敏感,并且在 Distortion-Based Penalization 中添加所有类别 (包括叶结点类别的父类) 的约束有助于提高模型性能
Learn from OpenReview of ICLR 2021
- 这篇文章也投过 ICLR 2021,下面学习一下部分 review 和作者的 rebuttal,主要集中于 review 中提到的主要缺陷。从 review 中也可以看出作者之后对论文做出了哪些改进
Final Decision – Reject
- Positive side: good motivation for the problem, a good ablation study and, in some cases, good performance over standard cross entropy.
- Negative side: limited novelty, missing discussion or comparison to prior work, and in some cases only marginal improvement over existing methods.
AnonReviewer1 – (Rating: 4: Ok but not good enough - rejection)
- Assumptions are not adequately discussed and results are inconclusive. (1) Guided-proto 在错误率指标上只在 4 个数据集中的 2 个上超过了 Learnt-proto,这说明 L d i s t o \mathcal L_{disto} Ldisto 并不能十分有效地提高准确率 (inconclusive results). (2) 如果模型目标是降低 Mistake severity 的话,那将 cost matrix D D D 设置成对称矩阵就是不合理的,例如在自动驾驶领域,将行人误分类为路灯带来的 cost 应该远大于将路灯误分类为行人的 cost,作者在论文中似乎混淆了类别相似度 “similarity” 和误分类 “cost”,“similarity” 与 “cost” 并不等价,类别层次树并不一定能反映出 cost of class confusions
- Reply to Reviewer 1. (1) 作者承认了没有仔细探讨 “similarity” 与 “cost” 之间的区别以及为什么对称的 cost matrix 有利于缓解 Mistake severity 问题,不过也指出论文中的 cost matrix 是从类别层次树中得到的,但论文所使用的方法可以推广到其他 cost matrix. (2) 作者认为论文重点是降低 AHC,从这个角度看, L d i s t o \mathcal L_{disto} Ldisto 在 4 个数据集中的 3 个上都是有效的。此外,Guided-proto 是唯一一种能在所有数据集和所有指标上都超过 CE baseline 的方法
- inconclusive results. Focusing on average hierarchical cost means additional information (the class hierarchy) is used. In other words, the authors are saying they use additional information and yet the performance degrades, and this normal?!
- Clarification. 作者认为错误率指标是建立在所有误分类 cost 相同的前提下的,引入 cost matrix 改变了这一前提,就可能会导致模型在错误率指标下表现得更差。Occasional improvement in ER are a fortuitous consequence of well-chosen hierarchies, and not benefit to expect systematically.
AnonReviewer2 – (Rating: 4: Ok but not good enough - rejection)
- Reinvention of several known concepts; small scientific contribution. (1) 作者没有引用有关 prototypical networks 的文献,考虑到 prototypical networks 领域的已有工作,Reviewer 认为这篇论文创新点不足
AnonReviewer3 – (Rating: 6: Marginally above acceptance threshold)
- Nice idea, providing consistent (small) accuracy improvements in well conducted experiments.
AnonReviewer4 – (Rating: 4: Ok but not good enough - rejection)
- Review. (1) innovation is limited, especially in light of missed recent works on prototype-based approaches using hierarchies in non-Euclidean spaces. Hyperbolic spaces are known to be a better fit for hierarchies.
[ICLR 2021] No cost likelihood manipulation at test time for making better mistakes in deep networks
- Karthik, Shyamgopal, et al. “No cost likelihood manipulation at test time for making better mistakes in deep networks.” ICLR (2021).
- code: https://github.com/sgk98/CRM-Better-Mistakes
Introduction
- 这篇文章的重点依然在于如何使用 label hierarchy 来降低模型犯错时的严重性 (i.e., Mistake severity issue). 作者提出了一种基于 条件风险最小化 (CRM) 的后处理方法,能在较小损失 Top-1 Acc 的情况下大幅降低 Avg. hier. dist. @ k k k ( k > 1 k>1 k>1),同时保证模型的可靠性 (i.e., Calibrated Model)
Approach
- 作者提出的方法极其简单,只是在推理时根据 Conditional Risk Minimisation (CRM) 进行决策,并不涉及任何训练时的 tricks.
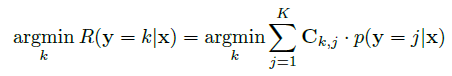 其中,
K
K
K 为类别数,
C
C
C 为 symmetric class-relationship matrix,
C
i
,
j
C_{i,j}
Ci,j 代表 the height of the lowest common ancestor
L
C
A
(
y
i
,
y
j
)
LCA(y_i, y_j )
LCA(yi,yj) between classes
i
i
i and
j
j
j (
C
i
,
j
C_{i,j}
Ci,j 越小,则类别越相似). The height of a node is defined as the number of edges between the given node and the furthest leaf.
其中,
K
K
K 为类别数,
C
C
C 为 symmetric class-relationship matrix,
C
i
,
j
C_{i,j}
Ci,j 代表 the height of the lowest common ancestor
L
C
A
(
y
i
,
y
j
)
LCA(y_i, y_j )
LCA(yi,yj) between classes
i
i
i and
j
j
j (
C
i
,
j
C_{i,j}
Ci,j 越小,则类别越相似). The height of a node is defined as the number of edges between the given node and the furthest leaf.
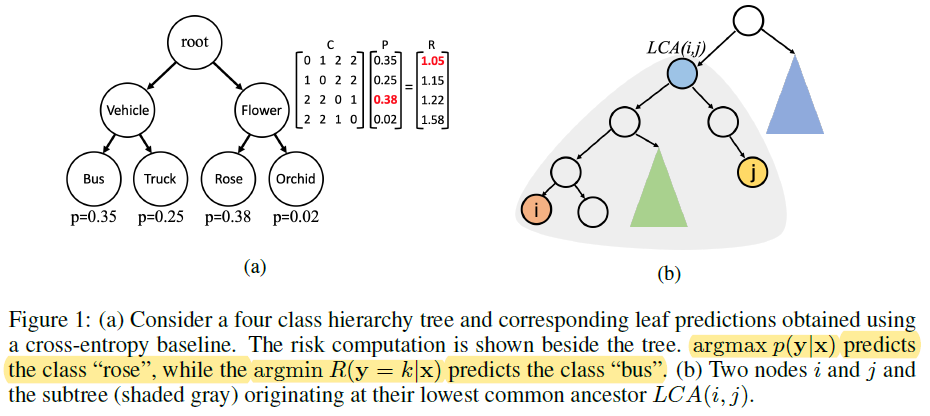
- CRM 还有一个比较合理的性质,就是深度学习模型通常具有 over-confident nature,对于大多数样本而言
max
p
(
y
∣
x
)
\max p(y|x)
maxp(y∣x) 都是超过 0.5 的,而此时 CRM decision 和 Bayes optimal decision 的 top-1 prediction 是一致的,也就是说,CRM 只有在模型不那么 confident 的时候才会根据 label hierarchy 去修正预测结果
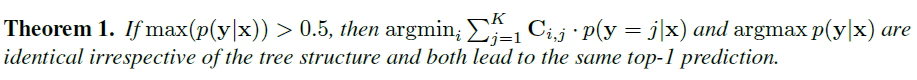 Proof
Proof

Experiments
Hierarchical Distance of Top-1 Predictions
- 作者首先指出了 Bertinetto, et al. 里提出的衡量 mistake severity 的指标 average mistake-severity metric 存在 bug. average mistake-severity 是指所有分类错误的样本对应的 mistake severity 的平均值,但在这一指标上表现更好的模型可能实际上并不是在 “make better mistakes”,而是在 “make additional low-severity mistakes” (对于 Bertinetto, et al. 里的两种方法,
β
\beta
β 越小,
α
\alpha
α 越大,这一倾向就越明显,high-severity mistakes 并没有明显减少,但 less-severe mistakes 却明显增多了,这也是在 average mistake-severity 上表现很好的模型,在 hierarchical distance@1 上却表现很差的原因)
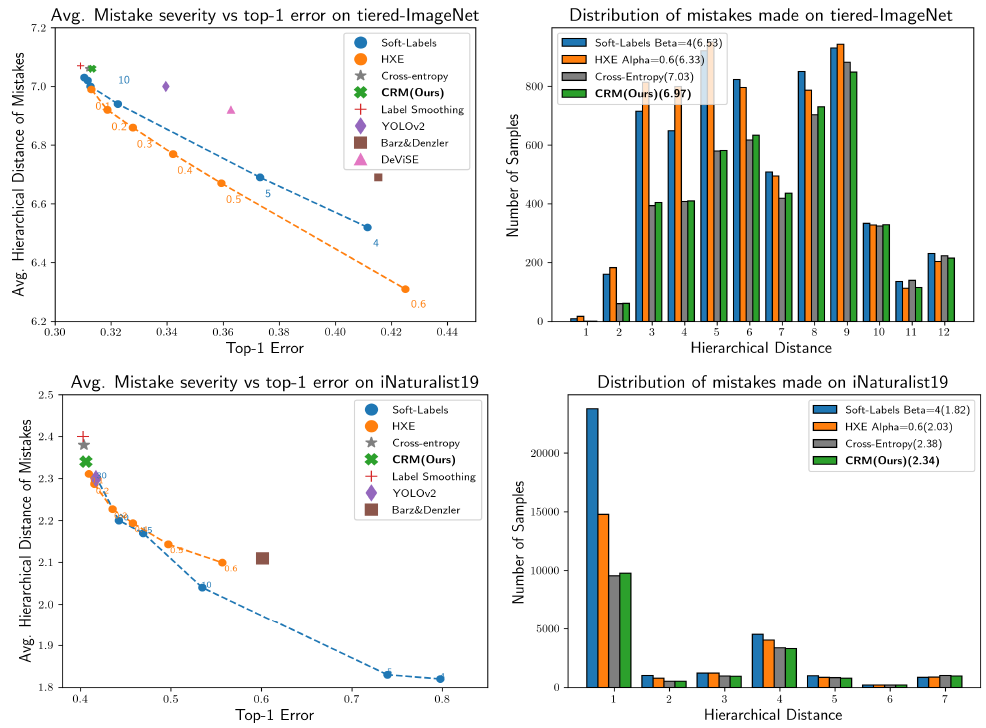
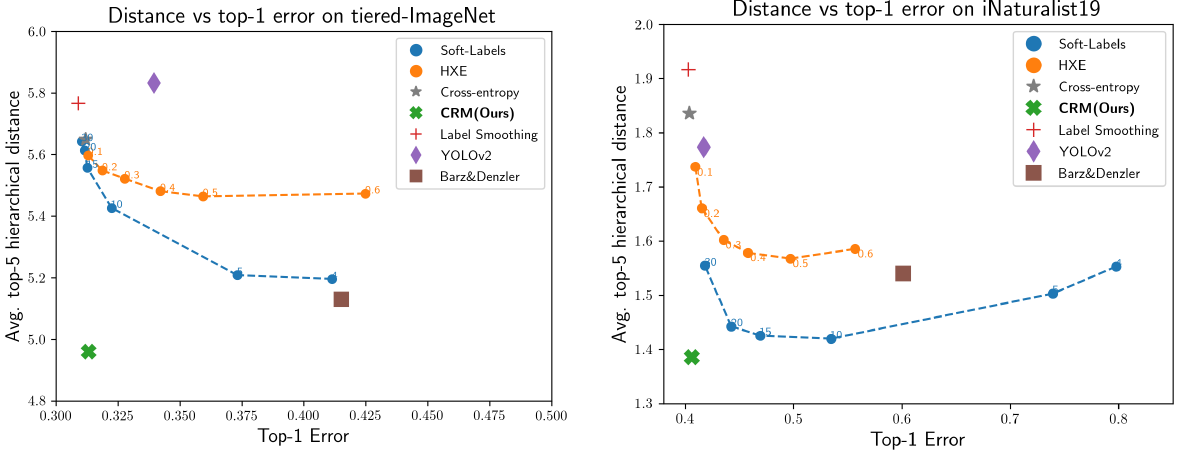
- 因此,作者采用的指标为 hierarchical distance@1 (computed over all the samples). 可以看到,CRM 相比 CE 略微降低了 mistake severity,但同时也降低了 Top-1 Acc. 另外也可以发现,仅针对 Top-1 预测结果而言,还没有方法能在 mistake severity 和 Top-1 Error 的 balance 上显著超过 CE
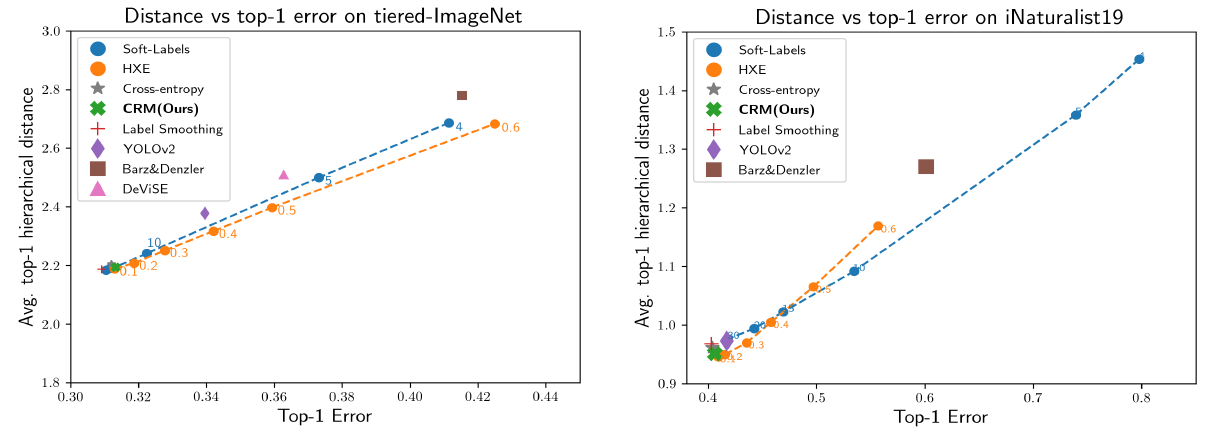
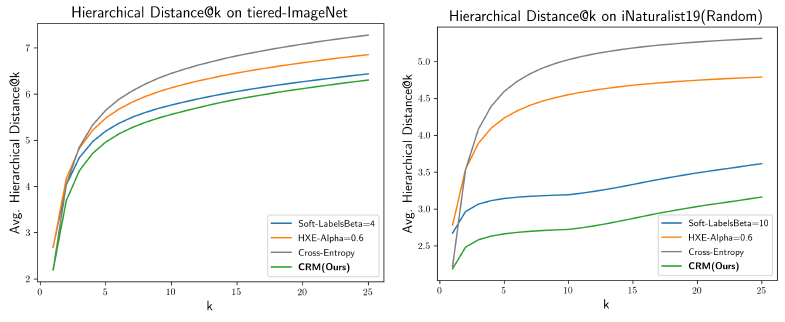
Hierarchical Distance of Top- k k k Predictions
- 作者使用 average hierarchical distance@
k
k
k 来评估预测结果的排序质量。在这一指标上,CRM 达到了 SOTA
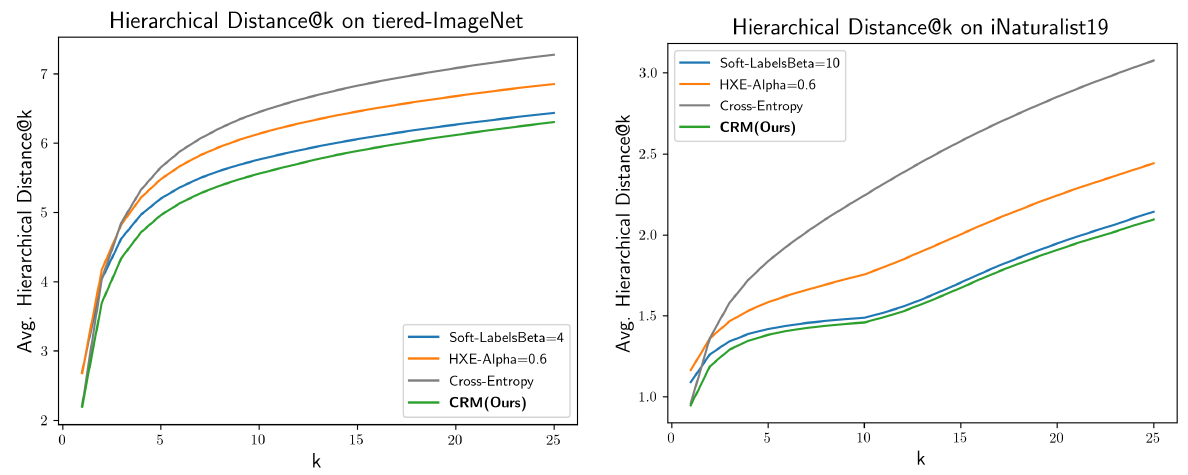 并且作者也发现,A better ranking of classes often comes with a significant trade-off with top-1 accuracy. 而 CRM 能在较少损失 top-1 performance 的情况下显著降低 average hierarchical distance@
k
k
k
并且作者也发现,A better ranking of classes often comes with a significant trade-off with top-1 accuracy. 而 CRM 能在较少损失 top-1 performance 的情况下显著降低 average hierarchical distance@
k
k
k
- 此外,作者还测试了在随机改变 hierarchy 时各个方法的性能 (因为在实际应用中,hierarchy 可能并不可靠). 结果表明,当 hierarchy 并不可靠时,CRM 仍然有效。而其余基于 hierarchy 训练的方法会使得不可靠的 hierarchy 阻碍模型训练
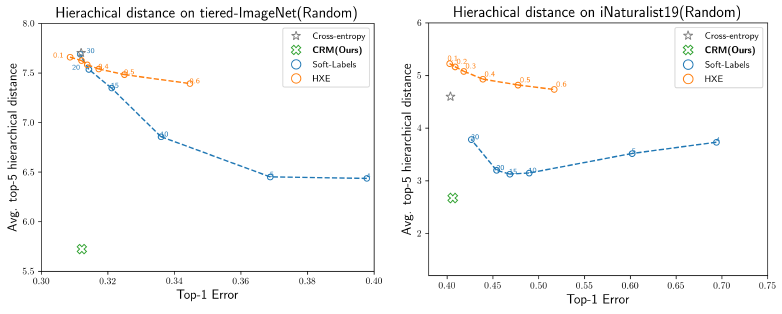
Impact of Label Hierarchy on the Reliability
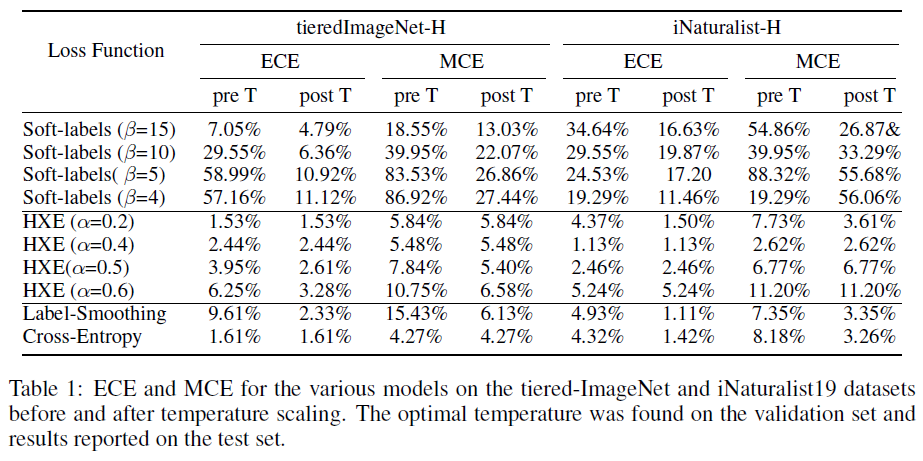
- 作者还比较了不同方法的 Calibration Error,指标采用 ECE (Expected Calibration Error) 和 MCE (Maximum Calibration Error). CRM does not hurt the calibration of a model as the cross-entropy likelihoods can still be used for the same
[ECCV 2022] Learning Hierarchy Aware Features for Reducing Mistake Severity
Introduction
- 为了解决 mistake severity issue 并尽量少得损害 Top-1 Acc,作者认为模型应该学得 Hierarchy-Aware Feature (HAF)
Hierarchy-Aware Feature (HAF)
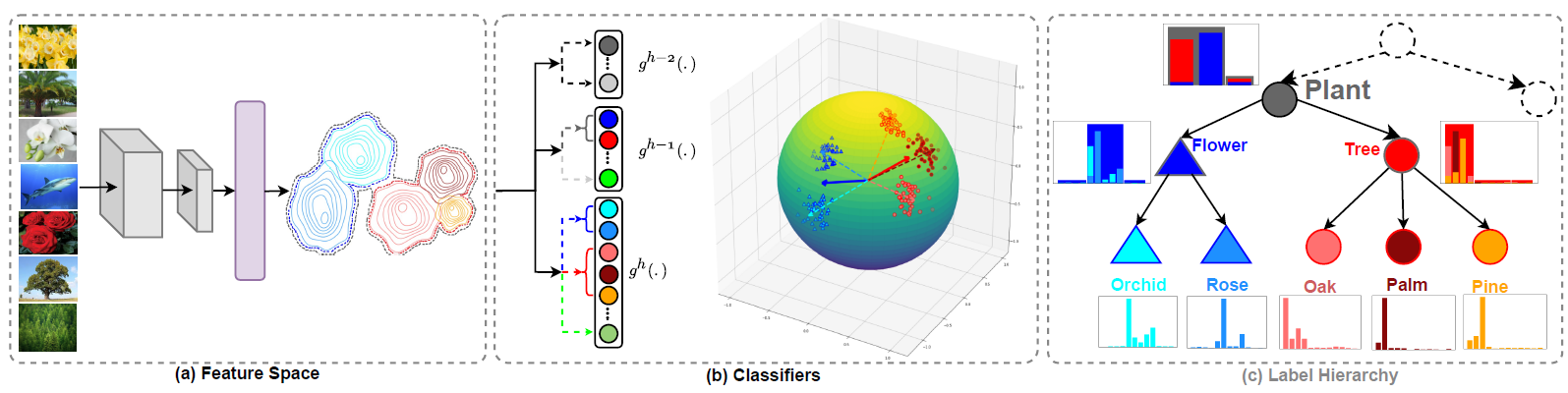
- 假设 label hierarchy tree 有
H
+
1
H+1
H+1 层,root 为 level-0. HAF 在每个层级上都设置一个 FC
W
h
W^h
Wh 作为 classifier
g
h
(
⋅
)
g^h(\cdot)
gh(⋅),它们共享 bacbone
f
ϕ
(
⋅
)
f_\phi(\cdot)
fϕ(⋅). 损失函数为:
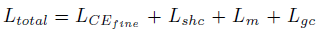
Fine Grained Cross-entropy ( L C E f i n e L_{CE_{fine}} LCEfine)
- HAF 只在最细粒度的层级
H
H
H 用 GT 标签计算 CE loss
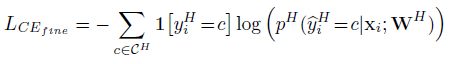 其中
p
H
(
y
^
i
H
=
c
∣
x
i
;
W
H
)
=
g
c
H
(
f
ϕ
(
x
i
)
)
p^H(\hat y_i^H=c\mid x_i;W^H)=g^H_c(f_\phi(x_i))
pH(y^iH=c∣xi;WH)=gcH(fϕ(xi)) 为模型输出的样本属于类别
c
c
c 的概率,
y
^
i
h
\hat y_i^h
y^ih 为模型输出的样本
i
i
i 在
h
h
h 类别层级上的概率分布,
h
h
h 类别层级对应的类别集合为
C
h
\mathcal C^h
Ch
其中
p
H
(
y
^
i
H
=
c
∣
x
i
;
W
H
)
=
g
c
H
(
f
ϕ
(
x
i
)
)
p^H(\hat y_i^H=c\mid x_i;W^H)=g^H_c(f_\phi(x_i))
pH(y^iH=c∣xi;WH)=gcH(fϕ(xi)) 为模型输出的样本属于类别
c
c
c 的概率,
y
^
i
h
\hat y_i^h
y^ih 为模型输出的样本
i
i
i 在
h
h
h 类别层级上的概率分布,
h
h
h 类别层级对应的类别集合为
C
h
\mathcal C^h
Ch
Soft Hierarchical Consistency ( L s h c L_{shc} Lshc)
- 我们希望不同层级的 classifier 输出的预测结果与 label hierarchy 一致。最简单的方法是对每个层级都用 CE loss 训练,但 Chang, et al. 指出,对粗粒度分类的学习实际上可能会损害模型的细粒度分类性能,因此作者使用细粒度分类器提供的 soft labels 来训练粗粒度分类器 (serves as a consistency regularization for the fine-grained classifier, thus leading to a reduction in severity of mistakes),这可以使得各个层级的 classifier 分类结果与标签层级保持一致。这也和知识蒸馏有点类似,相当于把细粒度分类器当作 teacher 去指导粗粒度分类器,并且如 Reversed Knowledge Distillation (Re-KD) 所述,student 的学习也可以反过来促进 teacher 的学习
- soft labels 的生成方式如下:The super-class target probability is the sum of its subclasses’ predicted probability.
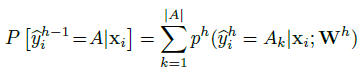 其中
A
A
A 为粗粒度层级
h
−
1
h-1
h−1 上的一个父类,
{
A
k
}
\{A_k\}
{Ak} (
1
≤
k
≤
∣
A
∣
1\leq k\leq |A|
1≤k≤∣A∣) 为细粒度层级
h
h
h 上
A
A
A 的子类
其中
A
A
A 为粗粒度层级
h
−
1
h-1
h−1 上的一个父类,
{
A
k
}
\{A_k\}
{Ak} (
1
≤
k
≤
∣
A
∣
1\leq k\leq |A|
1≤k≤∣A∣) 为细粒度层级
h
h
h 上
A
A
A 的子类
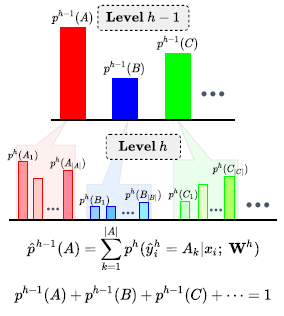
- 优化时使用 JS 散度
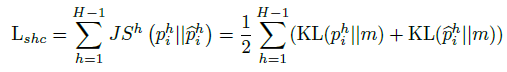 其中
p
i
h
p_i^h
pih 为粗粒度分类器预测结果,
p
^
i
h
\hat p_i^h
p^ih 为软标签,
m
−
1
2
(
p
i
h
+
p
^
i
h
)
m-\frac{1}{2}(p_i^h+\hat p_i^h)
m−21(pih+p^ih)
其中
p
i
h
p_i^h
pih 为粗粒度分类器预测结果,
p
^
i
h
\hat p_i^h
p^ih 为软标签,
m
−
1
2
(
p
i
h
+
p
^
i
h
)
m-\frac{1}{2}(p_i^h+\hat p_i^h)
m−21(pih+p^ih)
Margin Loss ( L m L_m Lm)
- 作者还使用了 pairwise margin-based loss 来促进 discrimination between coarse-level classes
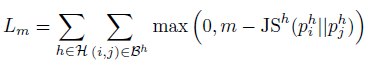 其中
H
=
[
k
,
H
−
1
]
\mathcal H=[k,H-1]
H=[k,H−1],
k
∈
[
1
,
H
−
1
]
k\in[1,H-1]
k∈[1,H−1] (i.e. Margin Loss 只在粗粒度层级上进行),
B
h
=
{
(
i
,
j
)
∣
y
i
h
≠
y
j
h
}
\mathcal B^h=\{(i,j)\mid y_i^h\neq y_j^h\}
Bh={(i,j)∣yih=yjh} 为层级
h
h
h 上标签不同的样本,
p
i
h
p^h_i
pih 为模型输出的层级
h
h
h 上样本
i
i
i 的类别概率分布
其中
H
=
[
k
,
H
−
1
]
\mathcal H=[k,H-1]
H=[k,H−1],
k
∈
[
1
,
H
−
1
]
k\in[1,H-1]
k∈[1,H−1] (i.e. Margin Loss 只在粗粒度层级上进行),
B
h
=
{
(
i
,
j
)
∣
y
i
h
≠
y
j
h
}
\mathcal B^h=\{(i,j)\mid y_i^h\neq y_j^h\}
Bh={(i,j)∣yih=yjh} 为层级
h
h
h 上标签不同的样本,
p
i
h
p^h_i
pih 为模型输出的层级
h
h
h 上样本
i
i
i 的类别概率分布
Geometric Consistency ( L g c L_{gc} Lgc)
- 作者还加入了 Geometric Consistency 来保证不同层级 classifier 的 weight 满足几何约束,使得粗粒度类别对应的 weight vector 和其子类的 weight vector 相关联
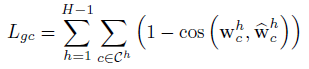 其中
C
h
\mathcal C^h
Ch 为层级
h
h
h 的类别集合,
w
c
h
w_c^h
wch 为粗粒度类别
c
c
c 对应的 normalized weight vector (i.e.,
∥
w
c
h
∥
2
=
1
\|w_c^h\|_2=1
∥wch∥2=1),
w
^
c
h
=
w
~
c
h
−
1
/
∥
w
~
c
h
−
1
∥
2
\hat w_c^{h}=\tilde w_c^{h-1}/\|\tilde w_c^{h-1}\|_2
w^ch=w~ch−1/∥w~ch−1∥2,
w
~
c
h
−
1
=
∑
k
∈
subclass
(
c
)
w
k
h
\tilde w_c^{h-1}=\sum_{k\in\text{subclass}(c)}w_{k}^h
w~ch−1=∑k∈subclass(c)wkh 为
c
c
c 的子类权重向量之和
其中
C
h
\mathcal C^h
Ch 为层级
h
h
h 的类别集合,
w
c
h
w_c^h
wch 为粗粒度类别
c
c
c 对应的 normalized weight vector (i.e.,
∥
w
c
h
∥
2
=
1
\|w_c^h\|_2=1
∥wch∥2=1),
w
^
c
h
=
w
~
c
h
−
1
/
∥
w
~
c
h
−
1
∥
2
\hat w_c^{h}=\tilde w_c^{h-1}/\|\tilde w_c^{h-1}\|_2
w^ch=w~ch−1/∥w~ch−1∥2,
w
~
c
h
−
1
=
∑
k
∈
subclass
(
c
)
w
k
h
\tilde w_c^{h-1}=\sum_{k\in\text{subclass}(c)}w_{k}^h
w~ch−1=∑k∈subclass(c)wkh 为
c
c
c 的子类权重向量之和
Experiments and Results
Datasets
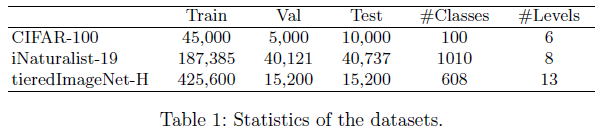
Results
- 几个注意点:(1) 实验进一步验证了 CRM 作为一种后处理方法是有效的,可以在尽量少地损失 Top-1 Acc 的情况下缓解 mistake severity issue;(2) CRM 的论文里已经说明了 Mistakes severity 存在 bug,因此这一指标必须结合 Top-1 Acc 一起分析;(3) 如果直接对比 HAF 和 CRM,其实可以发现 HAF 并不占优势… 不过 HAF + CRM 还是可以取得更好的效果;(4) 由于 Chang, et al. 是通过划分特征向量来对不同层级进行解耦,因此在类别层次数比较多时会损害 Top-1 Acc
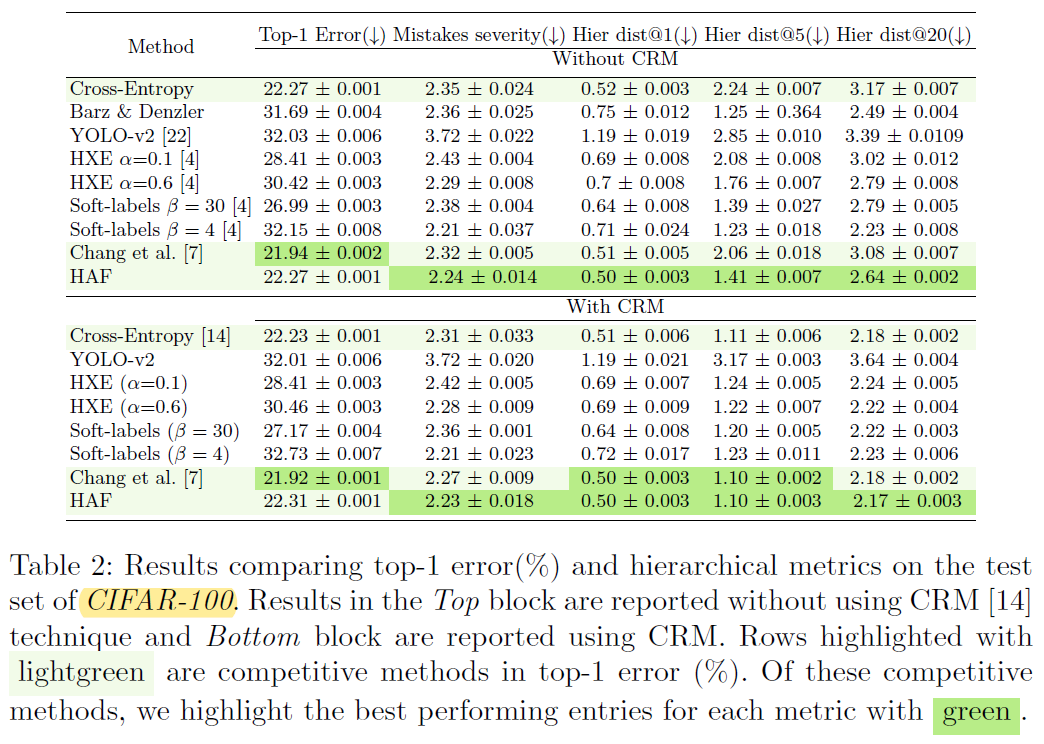
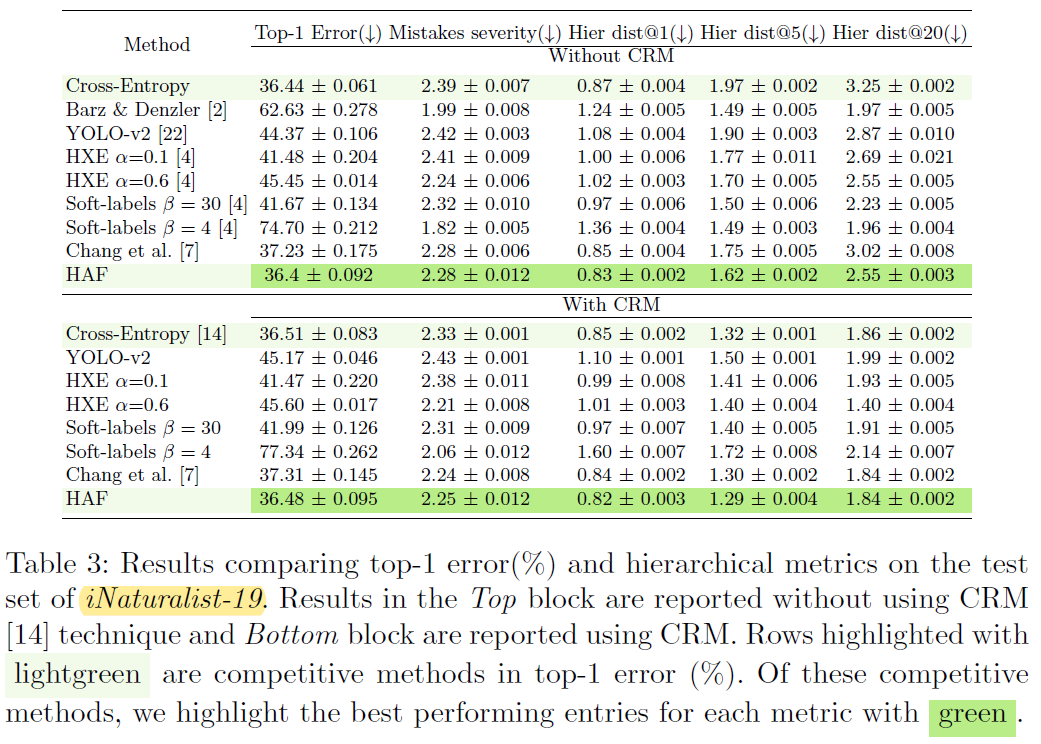
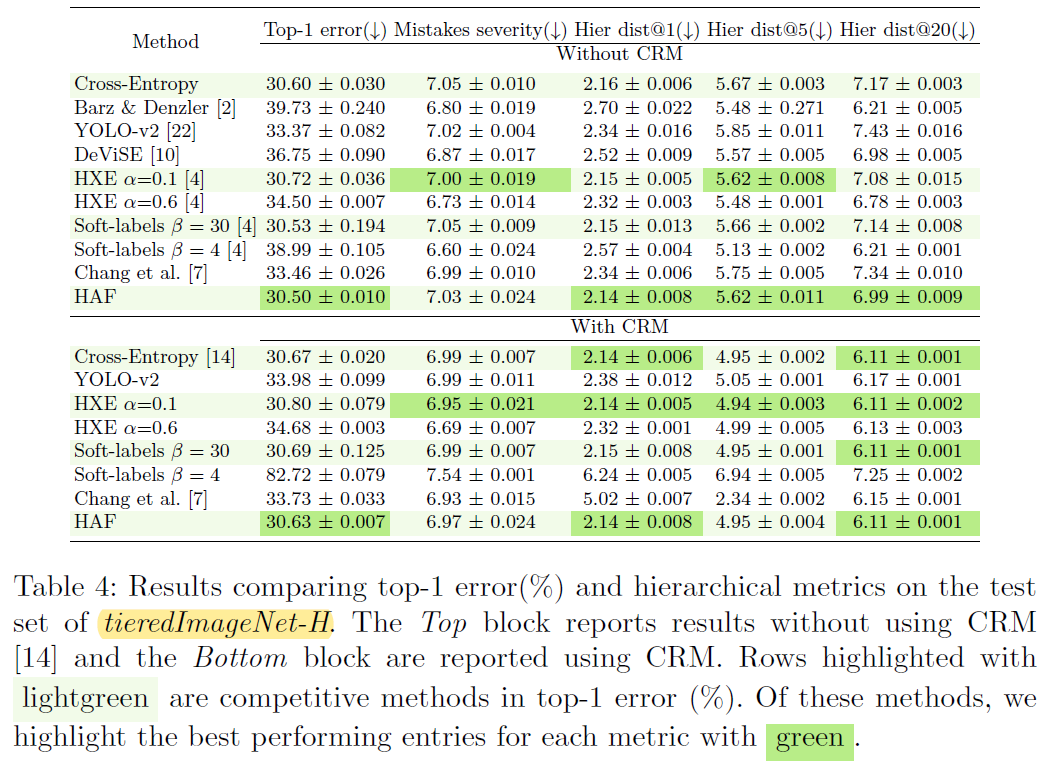
Coarse classification Accuracy
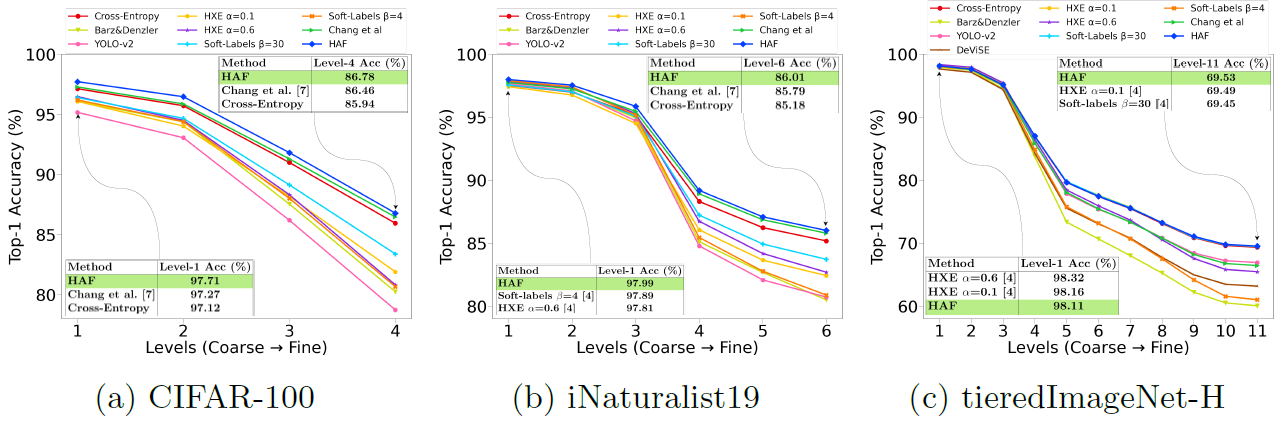
Ablation Study
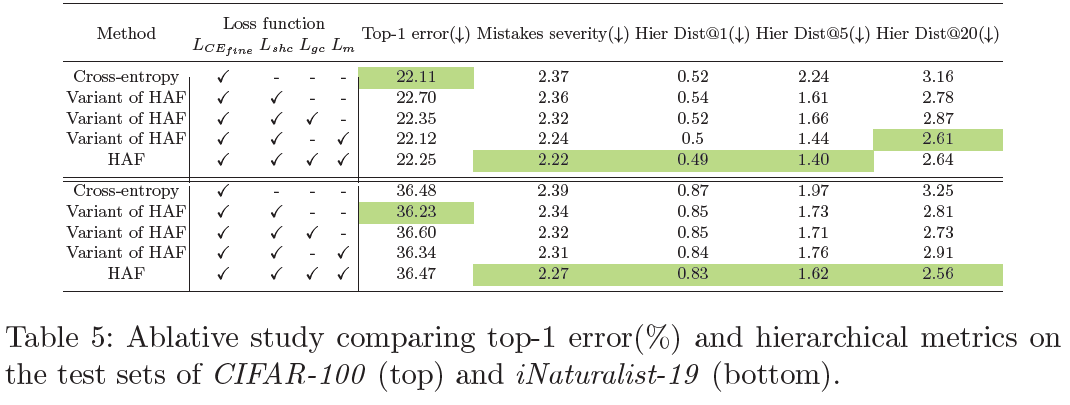
Mistakes Severity Plots
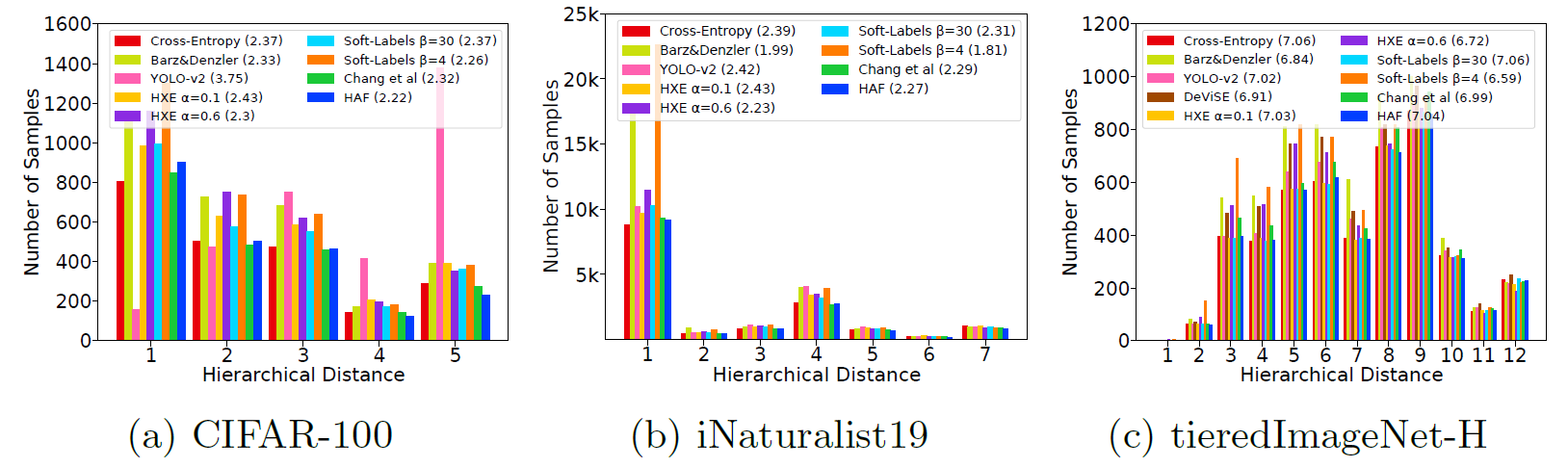
Discussion: Hierarchical Metrics
- 目前的 Hierarchical Metrics 都是 dependent on the label hierarchy tree,不能在多个数据集下统一比较,而是只能在同一数据集下比较相对数值大小。例如 tieredImageNet-H 数据集中每个类别的 minimum LCA 如下图所示,大多数类别的 minimum LCA 都大于 1 (which indicates a skewed hierarchy tree),这就会导致 tieredImageNet-H 数据集对应的 Hierarchical Metrics 数值总体比较大,而新方法又只能将部分错误样本的 LCA distance 减小,因此带来的提升量反映在数值上就会显得相对比较小
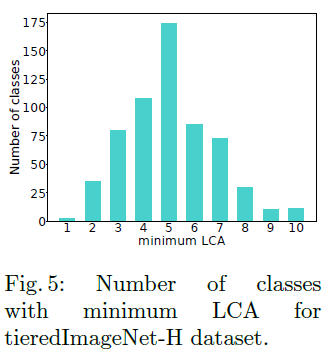
- 另外,对于只考虑 Top-1 预测结果的 Hierarchical Metrics,mistakes severity 可能会更偏向于 model with a large number of low-severity mistakes,average hierarchical distance@1 则可能会更偏向于 models with fewer overall mistakes,不足以反映 mistake’s severity. 相对理想的指标应该更加综合全面地考虑 Top-1 Acc 和 mistake’s severity
-
相关阅读:
AMD老电脑超频及性能提升方案及实施
27_Git&GitHub
【数仓日常踩坑】如何获取binlog数据里每个id的最新数据
从零开始学习 Java:简单易懂的入门指南之IO字符流(三十一)
线程(下):读写者模型\环形队列\线程池
MBatis-plus:架构使用
多维分析预汇总应该怎样做才管用?
Koa: 打造高效、灵活的Node.js后端 (介绍与环境部署)
java项目-第149期ssm师生交流平台_java毕业设计_计算机毕业设计
Android studio 常用的插件
- 原文地址:https://blog.csdn.net/weixin_42437114/article/details/128118188