T288401 B-莲子的机械动力学

专攻超统一物理学的莲子，对机械结构的运动颇有了解。如下图所示，是一个三进制加法计算器的（超简化）示意图。

一个四位的三进制整数，从低到高位，标为 x_1,x_2,x_3,x_4x1​,x2​,x3​,x4​。换言之，这个数可以写成 \overline{x_4x_3x_2x_1}_{(3)}x4​x3​x2​x1​​(3)​。把它放在这四个齿轮里，对应箭头指向的数字就是现在这位的数值。

在这种机械式计算机里，我们通过齿轮的啮合来实现数位间的连接。通过不同齿轮半径的比例来确定进制。图中所有浅灰色的小齿轮的半径，比上使用皮带相接的较大齿轮的半径，都是 1:31:3。那么小齿轮每转动一圈，大齿轮就转动 \dfrac{1}{3}31​ 圈，也就是刚好一个数码的角度。

于是，我们通过控制齿轮的半径实现了 33 进制的进位。

如果需要实现三进制加法，则只需要在对应数位拨动对应的数码长度即可。

如下是个例子，实现 \overline{1021}_{(3)}+\overline{0021}_{(3)}=\overline{1112}_{(3)}1021(3)​+0021(3)​=1112(3)​

初始时齿轮的状态如上。

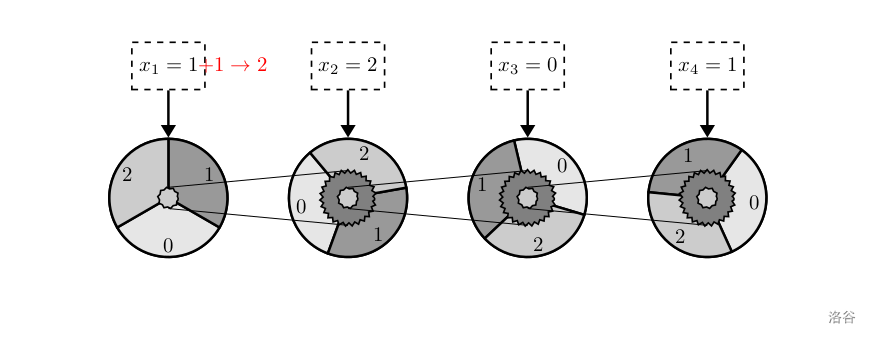
把第一个齿轮拨动一个单位长度，变为如上图所示。

把第二个齿轮拨动两个单位长度，变为如上图所示。读数，得到结果 \overline{1112}_{(3)}1112(3)​。

---

现在莲子设计了如下图所示的机械结构。对于从左往右数的第 ii 枚齿轮，它上面的浅色小齿轮与第 i+1i+1 枚齿轮上的深色小齿轮的半径之比为 1:(i+2)1:(i+2)。也就是说，第 ii 枚齿轮每转动 11 圈，第 i+1i+1 枚齿轮转过的角度恰好为它上面的一个数码。

莲子想要知道，在这样的特别的进制表示下，给定 a,ba,b，那么计算出的 a+ba+b 的结果是多少。

题目描述

题目背景的问题可以转化为如下描述：

给定两个长度分别为 n,mn,m 的整数 a,ba,b，计算它们的和。

但是要注意的是，这里的 a,ba,b 采用了某种特殊的进制表示法。最终的结果也会采用该种表示法。具体而言，从低位往高位数起，第 ii 位采用的是 i+1i+1 进制。换言之，相较于十进制下每一位的「逢 1010 进 11」，该种进制下第 ii 位是「逢 i+1i+1 进 11」。

下图所示，左边是十进制的竖式加法；右边是这种特殊进制的竖式加法。图中的红色加号表示上一位发生了进位。

输入格式

• 第一行有两个整数 n,mn,m，分别表示 aa 和 bb 的位数。
• 第二行有 nn 个整数，中间用空格隔开，从高到低位描述 aa 的每个数码。
• 第三行有 mm 个整数，中间用空格隔开，从高到低位描述 bb 的每个数码。

输出格式

• 输出有若干个整数，从高到低位输出 a+ba+b 在这种特殊表示法下的结果。

输入输出样例

输入 #1复制

5 4
3 3 2 1 1
3 2 2 1

输出 #1复制

4 2 1 1 0

输入 #2复制

10 1
10 9 8 7 6 5 4 3 2 1
0

输出 #2复制

10 9 8 7 6 5 4 3 2 1

说明/提示

对于全部数据，保证 1\le n,m\le 2\times 10^51≤n,m≤2×105，从低位往高位数起有 a_i\in[0,i]ai​∈[0,i]，b_i\in[0,i]bi​∈[0,i]。请使用 Java 或 Python 语言作答的选手注意输入输出时的效率。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
 
using namespace std;
 
 
//第二题
int main()
{
    long long n, m;
    cin >> n >> m;
    //找到n和m哪个大
    long long num;
    if(n >= m) num = n;
    else num = m;
    //初始化
    long long a[num+5], b[num+5], c[num+5];
    memset(a, 0, sizeof(a));
    memset(b, 0, sizeof(b));
    memset(c, 0, sizeof(c));
    //倒着输入
    for(long long i = n; i > 0; i--)
        cin >> a[i];
    for(long long i = m; i > 0; i--)
        cin >> b[i];
 
 
 
    long long i = 1;
 
 
    int sum;
    int out = 0;
    long long count1 = 2;
    bool haha = false;
    while(i <= num+1)
    {
        sum = (a[i]+b[i]+out)%count1; //获得该位的值
        out = (a[i]+b[i]+out)/count1; //获得下一位该进的值
        if(i == num && out >= 1) haha=true; //加起来是几位数
        //cout << sum << ' ' << out <
        count1++;
        c[i++] = sum; //用c数组存储该位的值（向后逆序存储）
    }
 
    if(haha == true)
    {
        for(long long k = num+1; k > 0; k--)
        {
            cout << c[k] << ' ';
        }
 
    }
    else
        for(long long k = num; k > 0; k--)
        {
            cout << c[k] << ' ';
        }
 
 
}