Java自幂数计算及其算法改进

1. 自幂数

如果在一个固定的进制中，一个n位自然数等于自身各个数位上数字的n次幂之和，则称此数为自幂数。
例如：在十进制中，153是一个三位数，各个数位的3次幂之和为1³⁺⁵3+3^3=153，所以153是十进制中的自幂数。
在n进制中，所有小于n的正整数都为自幂数，比如2进制中1是自幂数，3进制中1和2都是自幂数，4进制中1，2和3都是自幂数…

2.自幂数的个数

独身数共有9个: 1，2，3，4，5，6，7，8，9；
水仙花数共有4个：153，370，371，407；
四叶玫瑰数共有3个：1634，8208，9474；
五角星数共有3个：54748，92727，93084；
六合数只有1个：548834；
北斗七星数共有4个：1741725，4210818，9800817，9926315；
八仙数共有3个：24678050，24678051，88593477

3. 常规自幂数计算方法

package ui;

import javax.swing.*;

public class Test1 {
    public static void main(String[] args) {
        int count = 0;  //设计一个计数器来统计计算出来的自幂数的个数
        for (int i = 100; i < 999999999; i++) {  //计算一下999999999以内有游多少个自幂数
            int length = String.valueOf(i).length();  //获取当前计算整数的长度
            int sum = 0;  //定义整数，用来统计当前整数的每位数的幂次和
            int temp = i;  // 定义一个临时变量，该值将用于计算
            while(temp>0) {
                int a = temp%10;  // 取出当前数的最后一位，
                temp = temp/10;   // 将当前数除以10，得到余数
                sum+=Math.pow(a,length);  // 计算当前数的幂次和。
            }
            if(sum==i){  // 如果每位数的幂次和与i相等，则输出改数据。
                count++;  
                System.out.println(i);
            }
        }
        System.out.println("共计有 "+ count + " 个自幂数");
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

4.算法代码改进

第一种方法算到9位数的时候，就需要很长时间才能计算出下一位数。分析了算法，我们很多时间是使用在了调用Math.pow算法上，因为每一次循环都要去调用一下。
改进:我们可以将幂次方的结果放在一个数组中，每次使用的时候，都调用这个数组的值，而不用每次都重复计算一次。

package ui;

import javax.swing.*;

public class Test1 {
    public static void main(String[] args) {
    // 定义一个二维数组，将每一个一位整数的幂次方都计算保存到数组中。
        double[][] arr =  {{0,1,2,3,4,5,6,7,8,9},
                {0,1,Math.pow(2,2),Math.pow(3,2),Math.pow(4,2),Math.pow(5,2),Math.pow(6,2),Math.pow(7,2),Math.pow(8,2),Math.pow(9,2)},
                {0,1,Math.pow(2,3),Math.pow(3,3),Math.pow(4,3),Math.pow(5,3),Math.pow(6,3),Math.pow(7,3),Math.pow(8,3),Math.pow(9,3)},
                {0,1,Math.pow(2,4),Math.pow(3,4),Math.pow(4,4),Math.pow(5,4),Math.pow(6,4),Math.pow(7,4),Math.pow(8,4),Math.pow(9,4)},
                {0,1,Math.pow(2,5),Math.pow(3,5),Math.pow(4,5),Math.pow(5,5),Math.pow(6,5),Math.pow(7,5),Math.pow(8,5),Math.pow(9,5)},
                {0,1,Math.pow(2,6),Math.pow(3,6),Math.pow(4,6),Math.pow(5,6),Math.pow(6,6),Math.pow(7,6),Math.pow(8,6),Math.pow(9,6)},
                {0,1,Math.pow(2,7),Math.pow(3,7),Math.pow(4,7),Math.pow(5,7),Math.pow(6,7),Math.pow(7,7),Math.pow(8,7),Math.pow(9,7)},
                {0,1,Math.pow(2,8),Math.pow(3,8),Math.pow(4,8),Math.pow(5,8),Math.pow(6,8),Math.pow(7,8),Math.pow(8,8),Math.pow(9,8)},
                {0,1,Math.pow(2,9),Math.pow(3,9),Math.pow(4,9),Math.pow(5,9),Math.pow(6,9),Math.pow(7,9),Math.pow(8,9),Math.pow(9,9)},
                {0,1,Math.pow(2,10),Math.pow(3,10),Math.pow(4,10),Math.pow(5,10),Math.pow(6,10),Math.pow(7,10),Math.pow(8,10),Math.pow(9,10)},
                {0,1,Math.pow(2,11),Math.pow(3,11),Math.pow(4,11),Math.pow(5,11),Math.pow(6,11),Math.pow(7,11),Math.pow(8,11),Math.pow(9,11)},
                {0,1,Math.pow(2,12),Math.pow(3,12),Math.pow(4,12),Math.pow(5,12),Math.pow(6,12),Math.pow(7,12),Math.pow(8,12),Math.pow(9,12)}
        };

        int count = 0;
        for (int i = 100; i < 999999999; i++) {
            int length = String.valueOf(i).length();
            double sum = 0;
            int temp = i;
            while(temp>0) {
                int a = temp%10;
                temp = temp/10;
                sum+=arr[length-1][a];  // 取出二维数组中对应的数据，并与sum相加。
            }
            if(sum==i){
                count++;
                System.out.println(i);
            }
        }
        System.out.println("共计有 "+ count + " 个自幂数");
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

结果截图：
优化前的耗时为1213秒：

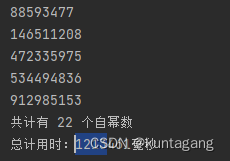
优化后的时间为46s，