Python排序：冒泡，选择，插入，希尔，归并，快速

编程中的交换元素逻辑：

 

# python中交换元素    有内置的三方底层逻辑 可以直接交换
a = 2
b = 3
a, b = b, a
print(a)      # a为3
 
# 其他编程需要有一个中间的变量来转换 变量设为temp
a = 2
b = 3
temp = a  
a = b
b = temp
print(a)      # a为3

-----冒泡排序-----

相邻元素，比较大小，如果顺序不符合规则，则交换位置。 

排好序的放后面，依次递减，直到第一位

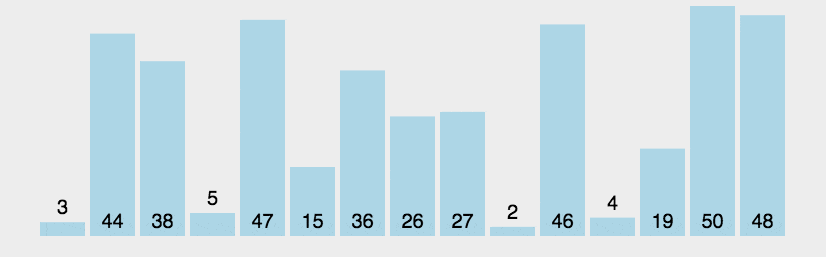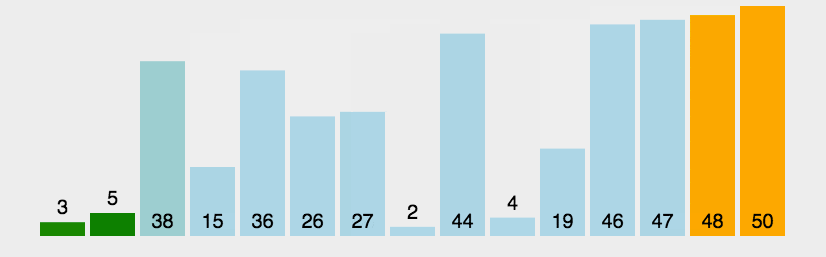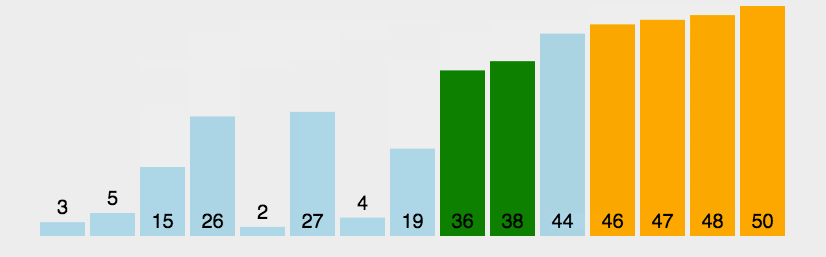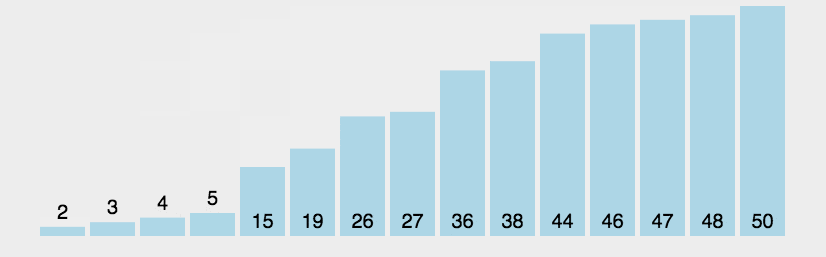
-----冒泡排序-----
 
list1 = [3, 6, 8, 1, 5, 4, 2]
print('list1原列表', list1)
for i in range(len(list1) - 1):
    for j in range(len(list1) - i - 1):
        if list1[j] > list1[j + 1]:  # 说明不符合(小--大)顺序，需要交换元素
            list1[j], list1[j + 1] = list1[j + 1], list1[j]
print('list1排序后', list1)

-----选择排序----- 

在未排序的序列中，找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中，继续寻找最小元素，放到已经排序序列的末尾。以此类推，直到所有元素均排序完毕。

-----选择排序-----
 
list2 = [3, 6, 8, 2, 5, 4, 1]
print('list2原列表', list2)
for i in range(len(list2) - 1):
    min_index = i
    for j in range(i + 1, len(list2)):  
        if list2[min_index] > list2[j]:  
            min_index = j  
    list2[min_index], list2[i] = list2[i], list2[min_index]
   
 
print('list2排序后', list2)

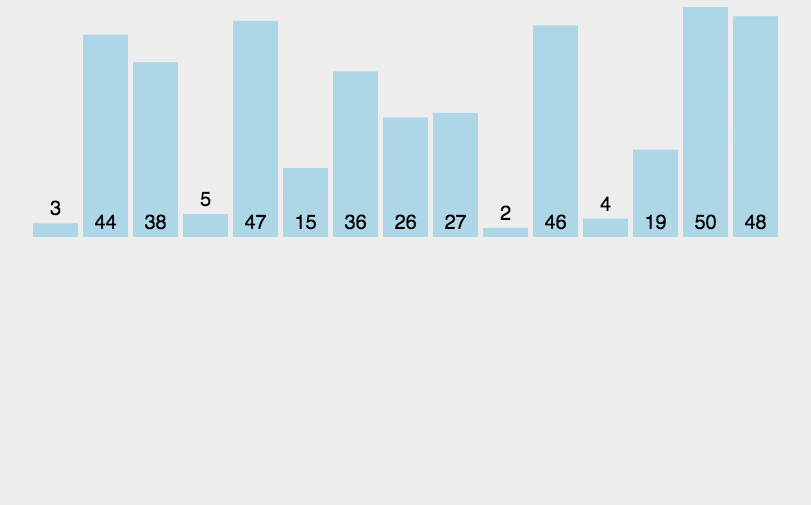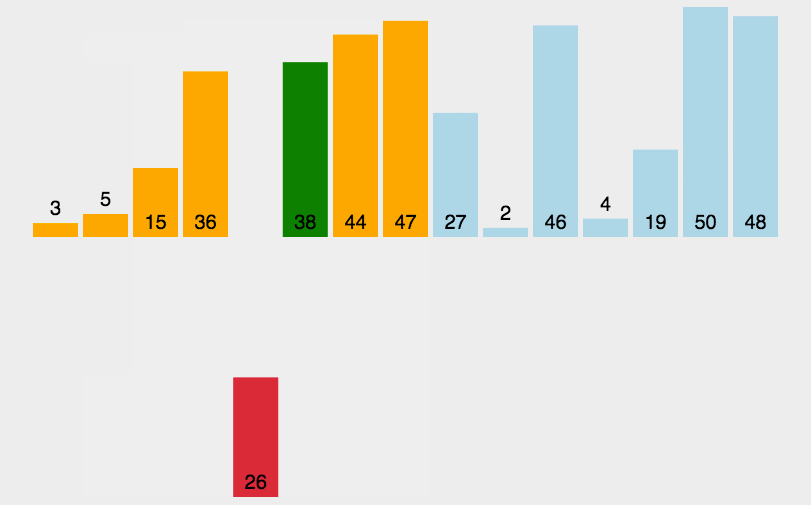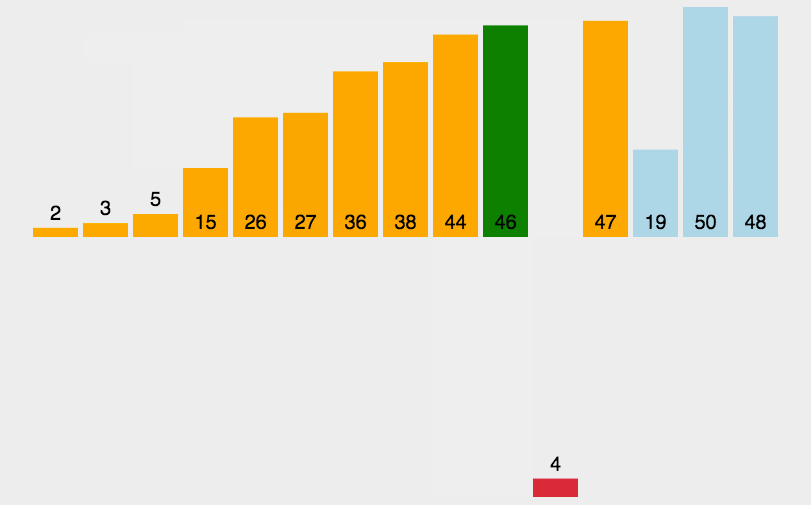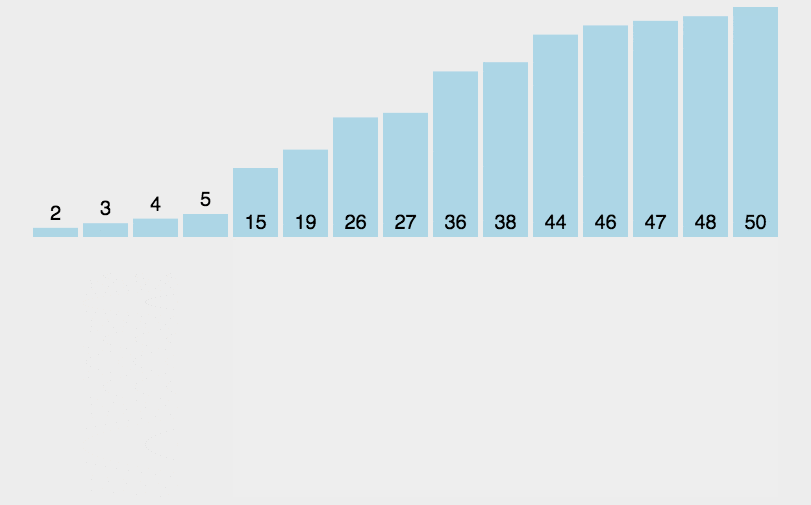
-----插入排序-----

构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

实现逻辑

① 从第一个元素开始，该元素可以认为已经被排序

② 取出下一个元素，在已经排序的元素序列中从后向前扫描

③如果该元素（已排序）大于新元素，将该元素移到下一位置

④ 重复步骤③，直到找到已排序的元素小于或者等于新元素的位置

⑤将新元素插入到该位置后

⑥ 重复步骤②~⑤

-----插入排序-----
 
def insertion_sort(arr):
    # 第一层for表示循环插入的遍数
    for i in range(1, len(arr)):
        # 当前需要插入的元素
        current = arr[i]
        # 相邻前面元素下标
        pre_index = i - 1
        # 索引>=0  当前要插入元素<前面元素
        while pre_index >= 0 and current < arr[pre_index]:
            # 前面元素索引往后移
            arr[pre_index + 1] = arr[pre_index]
            # pre_index赋值下一位前面元素的下标
            pre_index -= 1
        # 重新定义当前元素下标 为前面元素下标+1
        arr[pre_index + 1] = current
    return arr
 
 
list3 = [6, 3, 8, 2, 5, 4, 1]
B = insertion_sort(list3)
print(B)

-----希尔排序-----

排序的思想:将序列,分割为若干个子序列,每个序列做插入排序当整个序列基本有序,对整体做一次插入排序 

-----希尔排序-----缩小增量排序
 
def shell_sort(arr):
    # 取整计算增量(间隔)值
    gap = len(arr) // 2
    while gap > 0:
        # 从增量值开始遍历比较
        for i in range(gap, len(arr)):
            j = i 
            current = arr[i]  # 当前需要插入的元素
            # 索引>=0  当前元素<前面元素
            # arr[j - gap] 遍历前面元素的下标 - 增量值 = 对应前面元素的下标
            while j - gap >= 0 and current < arr[j - gap]:
                # 前面元素索引往后移
                arr[j] = arr[j - gap]
                # 赋值下一位前面元素的下标
                j -= gap
            # 重新定义当前元素下标 为前面元素下标+1
            arr[j] = current
        # 缩小增量（间隔）值
        gap //= 2
    return arr
 
 
list4 = [3, 6, 3, 18, 72, 55, 34, 1, 15, 18, 12, 11, 25]
sorted_arr = shell_sort(list4)
print(sorted_arr)

-----归并排序-----

归并排序采用分治法，思想是：先递归拆分数组为两半，再合并数组。

1、拆分数组

假设数组一共有 n 个元素，我们递归对数组进行折半拆分即n//2，直到每组只有一个元素为止。

2、合并数组

算法会从最小数组开始有序合并，这样合并出来的数组一直是有序的，所以合并两个有序数组是归并算法的核心

-----归并排序-----
 
def merge_sort(lst):
    # 递归结束条件
    if len(lst) <= 1:
        return lst
    # 分解问题，并递归调用
    middle = len(lst) // 2
    left = merge_sort(lst[:middle])
    right = merge_sort(lst[middle:])
 
    # 合并左右半部分，完成排序
    merged_lst = []
    # 在两个列表都有元素的情况下
    while left and right:
        # 比较左右第一个元素
        if left[0] <= right[0]:
            # 左边小 利用pop(0) 弹出第一个元素 进行添加
            merged_lst.append(left.pop(0))
        else:
            # 右边列表第一个元素小 添加右边
            merged_lst.append(right.pop(0))
    # 如果左部分或右部分还有剩余，那就拼接到排好序的列表中
    merged_lst.extend(right if right else left)
    return merged_lst
 
 
A = [11, 15, 88, 56, 13, 20, 44, 65, 28, 77, 40, 59, 83, 5, 80]
B = merge_sort(A)
print('待排序:', A)
print('已排序:', B)

-----快速排序-----

快速排序的基本原理是：

1. 先从数列中取出一个数作为基准数。(可以是第一个、最后一个、中间的或者干脆随机的）

2. 分区过程，将比这个数大的数全放到它的右边，小于的数全放到它的左边。

3. 再对左右区间重复第二步，直到各区间只有一个数。

-----快速排序-----
 
import random
 
 
class SortUtil():
    def quickSort(self, arr):
        if not arr:
            return arr
        pivot = random.choice(arr)
        equalList = []
        smallerList = []    # 存放小值
        biggerList = []    # 存放大值
        for item in arr:
            if item < pivot:
                smallerList.append(item)
            elif item == pivot:
                equalList.append(item)
            else:
                biggerList.append(item)
        # 每次返回小的或大的列表过去 进行下次分类排序
        return self.quickSort(smallerList) + equalList + self.quickSort(biggerList)
 
 
# 待排序列表
A = [3, 5, 59, 59, 25, 18, 46, 84, 15, 20, 33, 68]
KS = SortUtil()
sort_new = KS.quickSort(A)
print(sort_new)