dp入门（二）

目录

45、跳跃计划

53、最大子数组和

55、跳跃游戏

62、不同路径

 63、不同路径2

 64、最小路径和

 70、爬楼梯

 72、编辑距离

84、柱形图中最大的矩形

85、最大矩形

 4721、排队

---

45、跳跃计划

 

当前可移动距离尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最小步数。

思路虽然是这样，但在写代码的时候还不能真的就能跳多远跳远，那样就不知道下一步最远能跳到哪里了。

所以真正解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最小步数！

这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。

如果移动下标达到了当前这一步的最大覆盖最远距离了，还没有到终点的话，那么就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。

class Solution {
    public int jump(int[] nums) {
       int next = 0;
       int ans = 0;
       int end = 0;
        int n = nums.length;
        for (int i = 0; i < n - 1; i ++) {
           next = Math.max(next,nums[i] + i);
           if (i == end) {
               ans ++;
               end = next;
           }
        }
        return ans;
    }
}

53、最大子数组和

贪心思路：当我们连续子段和是负数时，我们是没必要留给下一个数的，因为下一个数不要这一段的和肯定更大，因此我们发现如果sum已经小于0了，我们就留给下一段一个0，每次更新最大值就行

class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        int res = Integer.MIN_VALUE;
        for (int i = 0,sum = 0; i < n; i ++) {
            sum += nums[i];
            res = Math.max(res,sum);
            if (sum < 0) sum = 0;
        }
        return res;
    }
}

动态规划：f[i] 表示nums中以i结尾的区间中最大和，f[i] 可以拆分为长度为1和长度大于1的区间，那么我们可以得到 f[i] 可以由 nums[i] 或者 f[i - 1] + nums[i]转移，两边取掉 nums[i],那就成了 nums[i - 1] + max(f[i - 1],0)，我们每次遇到的都是 f[i - 1] ，因此可以用 last 来替换！

class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        int res = Integer.MIN_VALUE;
        int last = 0;
        for (int i = 0; i < n; i ++) {
            last = Math.max(last,0) + nums[i];
            res = Math.max(res,last);
        }
        return res;
    }
}

55、跳跃游戏

 思路：暴力解法,记录我们可以到达的最远的点，如果我们到达了最远的点还不能到终点，就返回false ，否则返回true

class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;
        int end = 0;
        for (int i = 0; i < n; i ++) {
            end = Math.max(end,nums[i] + i);
            if (i == end && i != n - 1) return false; 
        }
        return true;
    }
}

62、不同路径

动态规划模板题，任何学动态规划的童鞋都不能没做过这道题！！！！

想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。

此时在回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j - 1]同理。

那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。

class Solution {
    public int uniquePaths(int m, int n) {
        int[] f = new int[n];
        for (int i = 0; i < m; i ++) {
            for (int j = 0; j < n; j ++) {
                if (i == 0 && j == 0) f[j] = 1;
                else if (j > 0) {
                    f[j] += f[j - 1];
                }
            }
        }
        return f[n - 1];
    }
}

加了维度压缩，因为是有一层是上一层转移,j 没变，但我记得比赛时候这题有可能爆int。。。。。

 63、不同路径2

 思路：一模一样，如果当前格子不是障碍物，它才有所谓的路径数量

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int n = obstacleGrid.length;
        int m = obstacleGrid[0].length;
        int[][] f = new int[n][m];
        for (int i = 0; i < n; i ++) {
            for (int j = 0; j < m; j ++) {
                if (obstacleGrid[i][j] == 0) {
                    if (i == 0 && j == 0) f[i][j] = 1;
                    else {
                        if (i > 0) f[i][j] += f[i - 1][j];
                        if (j > 0) f[i][j] += f[i][j - 1];
                    }
                }
            }
        }
        return f[n - 1][m - 1];
    }
}

 64、最小路径和

 思路：这三道题转移方程其实都是一样的，这道题唯一不同的点在于我们求得是最小值，不能让默认初始化为0干扰我们最终答案，因此我们初始化为无穷即可

class Solution {
    public int minPathSum(int[][] grid) {
        int n = grid.length;
        int m= grid[0].length;
        int[][] f = new int[n][m];
        for (int i = 0; i < n; i ++) Arrays.fill(f[i],0x3f3f3f3f);
        f[0][0] = grid[0][0];
        for (int i = 0; i < n; i ++) {
            for (int j = 0; j < m; j ++) {
                if (i > 0) f[i][j] = Math.min(f[i][j],f[i - 1][j] + grid[i][j]);
                if (j > 0) f[i][j] = Math.min(f[i][j],f[i][j - 1] + grid[i][j]);
            }
        }
        return f[n - 1][m - 1];
    }
}

 70、爬楼梯

 思路：同样的，我们f【i】可以由它的前一个（i - 1）跳一步或者 i - 2 （跳两步）得来，累加即可

class Solution {
    public int climbStairs(int n) {
        if (n == 0 || n == 1) return 1;
        int[] f = new int[n + 1];
        f[0] = 1;
        f[1] = 1;
        for (int i = 2 ; i <= n; i ++) {
            f[i] += f[i - 1] + f[i - 2];
        }
        return f[n];
    }
}

我们为了省空间可以用a,b来代替

class Solution {
    public int climbStairs(int n) {
        if (n == 0 || n == 1) return 1;
        int[] f = new int[n + 1];
        int a = 1;
        int b = 1;
        for (int i = 2 ; i <= n; i ++) {
            int c = a + b;
            a = b;
            b = c;
        }
        return b;
    }
}

 72、编辑距离

转移方程如上图所示，初始化记得我们每一个有意义字符串对应另一个字符串为0时的值应该时 有意义字符串的长度（删）

class Solution {
    public int minDistance(String word1, String word2) {
        int n = word1.length();
        int m = word2.length();
        word1 = " " + word1;
        word2 = " " + word2;
        int[][] f = new int[n + 1][m + 1];
        // for (int i = 0; i <= n; i ++) Arrays.fill(f[i],0x3f3f3f3f);
        for (int i = 1; i <= n; i ++) f[i][0] = i;
        for (int j = 1; j <= m; j ++) f[0][j] = j;
        for (int i = 1; i <= n; i ++) {
            for (int j = 1; j <= m; j ++) {
                f[i][j] = Math.min(f[i - 1][j],f[i][j - 1]) + 1;
                f[i][j] = Math.min(f[i][j],f[i - 1][j - 1] + (word1.charAt(i) == word2.charAt(j) ? 0 : 1));
            }
        }
        return f[n][m];
    }
}

为什么这里可以去掉初始化，因为我们更新最大值时没有用到它未更新时的状态，因此动态规划依然按照拓扑序

84、柱形图中最大的矩形

1、 此题的本质是找到每个柱形条左边和右边最近的比自己低的矩形条，然后用宽度乘上当前柱形条的高度作为备选答案。
2、解决此类问题的经典做法是单调栈，维护一个单调递增的栈，如果当前柱形条 i 的高度比栈顶要低，则栈顶元素 cur 出栈。出栈后，cur 右边第一个比它低的柱形条就是 i，左边第一个比它低的柱形条是当前栈中的 top。不断出栈直到栈为空或者柱形条 i 不再比 top 低。
3、满足 2 之后，当前矩形条 i 进栈。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        Stack stk = new Stack<>();
        int[] l = new int[n];
        int[] r = new int[n];
        for (int i = 0; i < n; i ++) {
            while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) stk.pop();
            if (stk.isEmpty()) l[i] = -1;
            else l[i] = stk.peek();
            stk.push(i);
        }
        stk.clear();
        for (int i = n - 1; i >= 0; i --) {
            while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) stk.pop();
            if (stk.isEmpty()) r[i] = n;
            else r[i] = stk.peek();
            stk.push(i);
        }
        int res = 0;
        for (int i = 0; i < n; i ++) {
            res = Math.max(res,(r[i] - l[i] - 1) * heights[i]);
        }
        return res;
    }
}

85、最大矩形

 

(单调栈) O(nm)O(nm)
1、将 Largest Rectangle in Histogram 问题扩展到二维。
2、一行一行考虑，类比 Largest Rectangle in Histogram，一行内所有柱形条的高度 heights 就是当前 (i, j) 位置能往上延伸的最大高度。
3、直接套用 Largest Rectangle in Histogram 的单调栈算法即可。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        Stack stk = new Stack<>();
        int[] l = new int[n];
        int[] r = new int[n];
        for (int i = 0; i < n; i ++) {
            while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) stk.pop();
            if (stk.isEmpty()) l[i] = -1;
            else l[i] = stk.peek();
            stk.push(i);
        }
        stk.clear();
        for (int i = n - 1; i >= 0; i --) {
            while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) stk.pop();
            if (stk.isEmpty()) r[i] = n;
            else r[i] = stk.peek();
            stk.push(i);
        }
        int res = 0;
        for (int i = 0; i < n; i ++) {
            res = Math.max(res,(r[i] - l[i] - 1) * heights[i]);
        }
        return res;
    }
 
 
    public int maximalRectangle(char[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        int[][] f = new int[n][m];
        for (int i = 0; i < n; i ++) {
            for (int j = 0; j < m; j ++) {
                if (matrix[i][j] == '1') {
                    if (i == 0) f[i][j] = 1;
                    else f[i][j] = 1 + f[i - 1][j];
                }
            }
        }
        int res = 0;
        for (int i = 0; i < n; i ++) res = Math.max(res,largestRectangleArea(f[i]));
        return res;
    }
}

 4721、排队

 

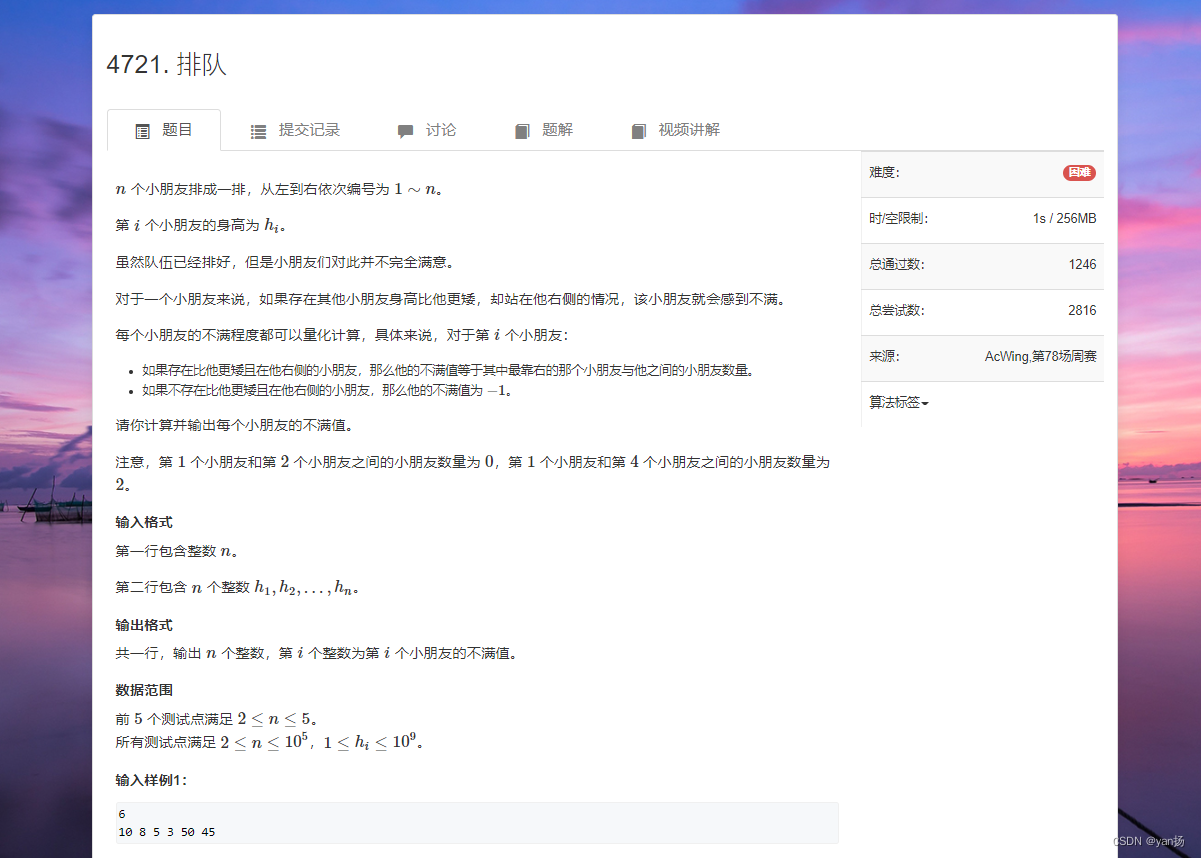
这道题是单调栈加二分的经典题目，以往的单调栈最常用是求我们最靠近且最小（大）的值，而本题中求的是；最远最小的值，因此我们要改变单调栈的添加顺序，从后往前，试想：如果存在一个靠左的数比靠右的数还大，那它是没有必要存在栈中的，因此栈中一定是从大到小的顺序，因此我们可以对每一个元素二分求小于它的数里边最大的一个

import java.util.*;
 
public class Main{
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] h = new int[n];
        for (int i = 0; i < n; i ++) h[i] = sc.nextInt();
        int top = 0;
        int[] stk = new int[n + 10];
        int[] res = new int[n];
        for (int i = n - 1; i >= 0; i --) {
            if (top == 0 || h[stk[top - 1]] >= h[i]) res[i] = -1;
            else {
                int l = 0;
                int r = top - 1;
                while (l < r) {
                    int mid = l + r >> 1;
                    if (h[stk[mid]] < h[i]) r = mid;
                    else l = mid + 1;
                }
                res[i] = stk[r] - i - 1;
            }
            if (top == 0 || h[i] < h[stk[top - 1]]) stk[top ++] = i;
        }
        for (int i = 0; i < n; i ++) {
            System.out.print(res[i] + " ");
        }
    }
}