数据结构学习笔记（Ⅲ）：栈和队列

目录

1 栈

1.1 栈的基本概念

1.定义

2.基本操作

​1.2 栈道顺序存储实现

1.实现 

2.基本操作

3.共享栈

1.3 栈的链式存储实现

2 队列

2.1 基本概念

1.定义

2.基本操作

2.2 队列的顺序实现

1.实现

2.基本操作

2.3 队列的链式实现

1.链式存储实现队列

2.基本操作

2.4 双端队列

1.双端队列

2.输入受限的双端队列

3.输出受限的双端队列

3 栈的应用

3.1 括号匹配问题

3.2 表达式求值

1.表达式

2.后缀表达式的计算

3.前缀表达式的计算

4.中缀表达式求值

3.3 递归应用

3.4 队列的应用

3.5 矩阵的压缩存储

1.数组的存储结构

2.对称矩阵的压缩存储

3.三角矩阵的压缩存储

4.三对角矩阵的压缩存储

5.稀疏矩阵的压缩存储

---

1 栈

1.1 栈的基本概念

1.定义

栈是只许在一段进行插入或删除的线性表。后进先出。

栈顶：允许插入和删除的一端

栈底：不允许插入和删除的一端

2.基本操作

1.2 栈道顺序存储实现

1.实现 

与顺序链表实现类似，需要将栈顶指针初始化。初始化时可以设置栈顶指针为-1或0

2.基本操作

以下基本操作时间复杂度：O(1)

入栈

出栈

读取栈顶元素

顺序栈的缺点：栈道大小不可变

3.共享栈

两个栈共享同一片空间

 栈满条件：top0 + 1 == top1;

1.3 栈的链式存储实现

只在头结点对单链表进行插入和删除操作就是栈道链式存储实现

2 队列

2.1 基本概念

1.定义

只允许在一端进行插入，另一端删除的线性表。先进先出

队尾：允许插入的一端

队头：允许删除的一端

2.基本操作

2.2 队列的顺序实现

1.实现

需要设置队头和队尾指针，初始化时可将指针指向0

2.基本操作

入队

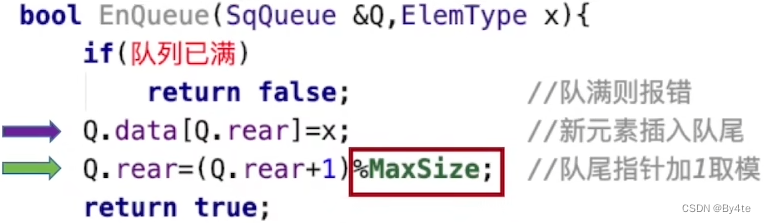
出队

查询

队满条件：(Q.rear + 1) % MaxSize == Q.front

队空条件：Q.rear == Q.front

也可在初始化时定义size，入队时size++，出队时size--，以判断队列

2.3 队列的链式实现

1.链式存储实现队列

 

2.基本操作

入队

出队

链式存储一般不会队满

2.4 双端队列

1.双端队列

允许从两端插入和删除的线性表

2.输入受限的双端队列

允许从两端删除、从一端插入的队列

3.输出受限的双端队列

允许从两段插入、从一端删除的队列

单端序列：n个输入的卡特兰数即合法的出栈序列

3 栈的应用

3.1 括号匹配问题

扫描到左括号就入栈，扫描到右括号且栈为空时匹配失败，不为空时栈顶元素出栈与扫描到的元素尝试匹配

3.2 表达式求值

1.表达式

中缀表达式：运算符在两个操作数之间

后缀表达式：运算符在两个操作数之后

前缀表达式：运算符在两个操作数之前 

2.后缀表达式的计算

左优先原则：只要左边的运算符能先计算，就优先算左边的，可以保证运算顺序唯一

3.前缀表达式的计算

右优先原则：只要右边的运算符能先计算，就优先算右边的，可以保证运算顺序唯一

4.中缀表达式求值

3.3 递归应用

函数调用时，最后被调用的函数最先执行结束。

递归调用时，函数调用栈可称为“递归工作栈”。每进入一层递归，就将递归调用所需信息压入栈顶；每退出一层递归，就从栈顶弹出相应信息。

3.4 队列的应用

树的层次遍历、图的广度优先遍历、操作系统中应用

3.5 矩阵的压缩存储

1.数组的存储结构

一维数组元素大小相同，且物理上连续存放；二维数组包括行优先和列优先存储方式。 普通矩阵可以使用数组的形式存储

2.对称矩阵的压缩存储

只存储主对角线和三角区数据，按行优先将各元素存入一维数组中。

矩阵下标-->一维数组下标

3.三角矩阵的压缩存储

将主对角线和非常量区元素存储在一维数组中，并在数组末尾存放常量

4.三对角矩阵的压缩存储

按行/列优先原则，只存储带状部分

5.稀疏矩阵的压缩存储

非零元素个数远小于矩阵元素个数

 按顺序存储--行、列、值的方式存储矩阵元素

按十字链表法：