Bezier曲线与B-Spline曲线

微分几何基础

微分集合是用微分的方法来研究曲线的局部性质，如曲线的弯曲程度等。
一条可以用参数表示的三维曲线是一个有界点集，可以写成一个带参数的、连续的、单值的数学函数：
{ x = x ( t ) y = y ( t ) z = z ( t ) 0 ⩽ t ⩽ 1 p = p ( t ) t ∈ [ 0 , 1 ] p ′ ( t ) = d p d t p ′ ′ ( t ) = d 2 p d t 2

​⎩⎪⎨⎪⎧​x=x(t)y=y(t)z=z(t)​0⩽t⩽1p=p(t)t∈[0,1]p′(t)=dtdp​p′′(t)=dt2d2p​​

位置矢量

贝塞尔曲线

一阶贝塞尔曲线$P_0^1$由两个控制点$P_0$和$P_1$完全定义，相当于线性插值。随着$t$从0到1变化，贝塞尔点从$P_0$移动到$P_1$.
$$P_0^1=\left(1-t\right)P_0+t{P}_1,t\in [0,1]$$

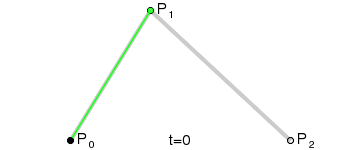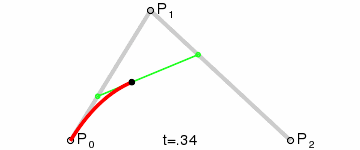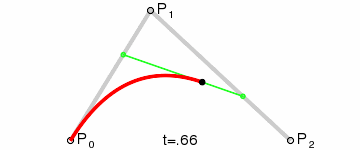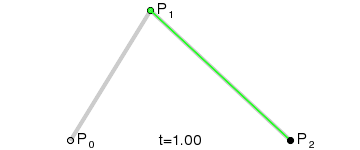
二阶贝塞尔曲线由一阶贝塞尔曲线递归定义。三个控制点$P_0$、$P_1$、$P_2$，二阶贝塞尔曲线的产生完全由这三个点的位置决定。
三个控制点每两个相邻的控制点产生一个一阶贝塞尔点，两个一阶贝塞尔点，于是得到两个点；
两个点形成一个线段，这个线段上有一个点在运动，于是得到一个点；
P 1 1 = ( 1 − t ) P 1 + t P 2 P 0 2 = ( 1 − t ) P 0 1 + t P 1 1 = ( 1 − t ) [ ( 1 − t ) P 0 + t P 1 ] + t [ ( 1 − t ) P 1 + t P 2 ] = P 0 ( 1 − t ) 2 + 2 P 1 t ( 1 − t ) + P 2 t 2

P11​P02​​=(1−t)P1​+tP2​=(1−t)P01​+tP11​=(1−t)[(1−t)P0​+tP1​]+t[(1−t)P1​+tP2​]=P0​(1−t)2+2P1​t(1−t)+P2​t2​
三阶贝塞尔曲线：
$$P_0^3=P_0{\left(1-t\right)}^3+3P_{1}t\left(1-t\right)+3P_{2}t\left(1-t\right)+P_2{t}^3$$

通用递归定义公式：

P i k = { P i k = 0 ( 1 − t ) P i k − 1 + t P i + 1 k − 1 k ⩾ 1 P_{i}^{k}=

Pik​={Pi​(1−t)Pik−1​+tPi+1k−1​​k=0k⩾1​
总结规律可得n阶贝塞尔曲线的公式为：
$$P_i^n=\sum _{j=0}^n{C}_n^j{\left(1-t\right)}^{n-j}{t}^j{P}_{i+j}t\in [0,1]$$
使用数学归纳法证明：

假设$n⩽k$时如下等式成立
$$P_i^k=\sum _{j=0}^k{C}_k^j{\left(1-t\right)}^{k-j}{t}^j{P}_{i+j}$$
当$n=k+1$时，
P i k + 1 = ( 1 − t ) P i k + t P i + 1 k . = ( 1 − t ) ∑ j = 0 k C k j ( 1 − t ) k − j t j P i + j + t ∑ j = 0 k C k j ( 1 − t ) k − j t j P i + j + 1 = ∑ j = 0 k C k j ( 1 − t ) k − j + 1 t j P i + j + ∑ j = 1 k + 1 C k j − 1 ( 1 − t ) k − j + 1 t j P i + j = ( 1 − t ) k + 1 + [ ∑ j = 1 k ( C k j + C k j − 1 ) ( 1 − t ) k − j + 1 t j P i + j ] + C k k t k + 1

Pik+1​​=(1−t)Pik​+tPi+1k​.=(1−t)j=0∑k​Ckj​(1−t)k−jtjPi+j​+tj=0∑k​Ckj​(1−t)k−jtjPi+j+1​=j=0∑k​Ckj​(1−t)k−j+1tjPi+j​+j=1∑k+1​Ckj−1​(1−t)k−j+1tjPi+j​=(1−t)k+1+[j=1∑k​(Ckj​+Ckj−1​)(1−t)k−j+1tjPi+j​]+Ckk​tk+1​
因为
C k + 1 j = ( k + 1 ) ! ( k + 1 − j ) ! j ! C k j = k ! ( k − j ) ! j ! C k j − 1 = k ! ( k − j + 1 ) ! ( j − 1 ) ! C k j + C k j − 1 = k ! ( k − j ) ! ( j − 1 ) ! ( 1 j + 1 k − j + 1 ) = k ! ⋅ ( k + 1 ) [ ( k − j ) ! ⋅ ( k − j + 1 ) ] ⋅ [ ( j − 1 ) ! ⋅ j ] = ( k + 1 ) ! ( k + 1 − j ) ! j ! = C k + 1 j

Ck+1j=(k+1)!(k+1−j)!j!Ckj=k!(k−j)!j!Ckj−1=k!(k−j+1)!(j−1)!Ckj+Ckj−1=k!(k−j)!(j−1)!(1j+1k−j+1)=k!⋅(k+1)[(k−j)!⋅(k−j+1)]⋅[(j−1)!⋅j]=(k+1)!(k+1−j)!j!=Ck+1j" role="presentation">Cjk+1CjkCj−1kCjk+Cj−1k=(k+1)!(k+1−j)!j!=k!(k−j)!j!=k!(k−j+1)!(j−1)!=k!(k−j)!(j−1)!(1j+1k−j+1)=k!⋅(k+1)[(k−j)!⋅(k−j+1)]⋅[(j−1)!⋅j]=(k+1)!(k+1−j)!j!=Cjk+1$$\begin{array}{rl}{C}_{k+1}^j& ={\displaystyle \frac{\left(k+1\right)!}{\left(k+1-j\right)!j!}}\\ C_k^j& ={\displaystyle \frac{k!}{\left(k-j\right)!j!}}\\ C_k^{j-1}& ={\displaystyle \frac{k!}{\left(k-j+1\right)!\left(j-1\right)!}}\\ C_k^j+C_k^{j-1}& ={\displaystyle \frac{k!}{\left(k-j\right)!\left(j-1\right)!}}\left({\displaystyle \frac{1}{j}}+{\displaystyle \frac{1}{k-j+1}}\right)\\ & ={\displaystyle \frac{k!\cdot \left(k+1\right)}{\left[\left(k-j\right)!\cdot \left(k-j+1\right)\right]\cdot \left[\left(j-1\right)!\cdot j\right]}}\\ & ={\displaystyle \frac{\left(k+1\right)!}{\left(k+1-j\right)!j!}}=C_{k+1}^j\end{array}$$

Ck+1j​Ckj​Ckj−1​Ckj​+Ckj−1​​=(k+1−j)!j!(k+1)!​=(k−j)!j!k!​=(k−j+1)!(j−1)!k!​=(k−j)!(j−1)!k!​(j1​+k−j+11​)=[(k−j)!⋅(k−j+1)]⋅[(j−1)!⋅j]k!⋅(k+1)​=(k+1−j)!j!(k+1)!​=Ck+1j​​
所以
$$P_i^{k+1}=\sum _{j=0}^{k+1}{C}_{k+1}^j{\left(1-t\right)}^{k-j+1}{t}^j{P}_{i+j}$$

贝塞尔曲线的性质：

1. 各项系数之和为1
   $$\sum _{j=0}^n{C}_n^j{\left(1-t\right)}^{n-j}{t}^j=(1-t+t{)}^n=1$$
2. 凸包性
   由性质1可知贝塞尔曲线是控制点的凸组合，所以贝塞尔曲线始终包含在所有控制点组成的最小凸多边形中。也就是可以通过控制点的凸包来限制规划曲线的范围，这在路径规划中是很好的一条性质。
3. 端点性质
   第一个控制点和最后一个控制点，恰好是曲线的起始点和终止点。可以将$t=1$或$0$代入，除了起始点和终止点的其他控制点的系数都是0。
4. 一阶导数性质：贝塞尔曲线在$t=0$时的导数与$P_i{P}_{i+1}$方向相同，在$t=1$时的导数与$P_{i+n-1}{P}_{i+n}$方向相同
   d P i n d t = d ( 1 − t ) n d t P i + ∑ j = 1 n − 1 C n j P i + j [ ( 1 − t ) n − j d t j d t + d ( 1 − t ) n − j d t t j ] + d t n d t P n = − n ( 1 − t ) n − 1 P i + n t n − 1 P i + n + ∑ j = 1 n − 1 C n j P i + j [ j ( 1 − t ) n − j t j − 1 − ( n − j ) ( 1 − t ) n − j − 1 t j ]
   dPindt=d(1−t)ndtPi+∑j=1n−1CnjPi+j[(1−t)n−jdtjdt+d(1−t)n−jdttj]+dtndtPn=−n(1−t)n−1Pi+ntn−1Pi+n+∑j=1n−1CnjPi+j[j(1−t)n−jtj−1−(n−j)(1−t)n−j−1tj]" role="presentation">dPnidt=d(1−t)ndtPi+∑j=1n−1CjnPi+j[(1−t)n−jdtjdt+d(1−t)n−jdttj]+dtndtPn=−n(1−t)n−1Pi+ntn−1Pi+n+∑j=1n−1CjnPi+j[j(1−t)n−jtj−1−(n−j)(1−t)n−j−1tj]$$\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{P}_i^n}{\mathrm{d}t}}& ={\displaystyle \frac{\mathrm{d}{\left(1-t\right)}^n}{\mathrm{d}t}}{P}_i+\sum _{j=1}^{n-1}{C}_n^j{P}_{i+j}\left[{\left(1-t\right)}^{n-j}{\displaystyle \frac{\mathrm{d}{t}^j}{\mathrm{d}t}}+{\displaystyle \frac{\mathrm{d}{\left(1-t\right)}^{n-j}}{\mathrm{d}t}}{t}^j\right]+{\displaystyle \frac{\mathrm{d}{t}^n}{\mathrm{d}t}}{P}_n\\ & =-n{\left(1-t\right)}^{n-1}{P}_i+n{t}^{n-1}{P}_{i+n}+\sum _{j=1}^{n-1}{C}_n^j{P}_{i+j}\left[j{\left(1-t\right)}^{n-j}{t}^{j-1}-\left(n-j\right){\left(1-t\right)}^{n-j-1}{t}^j\right]\end{array}$$
   dtdPin​​​=dtd(1−t)n​Pi​+j=1∑n−1​Cnj​Pi+j​[(1−t)n−jdtdtj​+dtd(1−t)n−j​tj]+dtdtn​Pn​=−n(1−t)n−1Pi​+ntn−1Pi+n​+j=1∑n−1​Cnj​Pi+j​[j(1−t)n−jtj−1−(n−j)(1−t)n−j−1tj]​
   d P i n d t ∣ t = 0 = − n P i + C n 1 P i + 1 = n ( P i + 1 − P i ) d P i n d t ∣ t = 1 = n P i + n − C n n − 1 P i + n − 1 = n ( P i + n − P i + n − 1 )
   dPindt|t=0=−nPi+Cn1Pi+1=n(Pi+1−Pi)dPindt|t=1=nPi+n−Cnn−1Pi+n−1=n(Pi+n−Pi+n−1)" role="presentation">dPnidt|t=0dPnidt|t=1=−nPi+C1nPi+1=n(Pi+1−Pi)=nPi+n−Cn−1nPi+n−1=n(Pi+n−Pi+n−1)$$\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{P}_i^n}{\mathrm{d}t}}{|}_{t=0}& =-n{P}_i+C_n^1{P}_{i+1}=n\left(P_{i+1}-P_i\right)\\ {\displaystyle \frac{d{P}_i^n}{dt}}{|}_{t=1}& =n{P}_{i+n}-C_n^{n-1}{P}_{i+n-1}=n\left(P_{i+n}-P_{i+n-1}\right)\end{array}$$
   dtdPin​​∣t=0​dtdPin​​∣t=1​​=−nPi​+Cn1​Pi+1​=n(Pi+1​−Pi​)=nPi+n​−Cnn−1​Pi+n−1​=n(Pi+n​−Pi+n−1​)​

分段贝塞尔曲线

虽然贝塞尔曲线的阶数可以很高，但是如果曲线的阶数过高，调整控制点对曲线的影响就比较小，调整起来相当麻烦。
于是，我们常常使用分段的贝塞尔曲线，保证每一小段不会太复杂。这样每次只用调小段，还可以做到只调局部不影响大局，那就相当舒服了。

分段带来的唯一问题是，曲线在段与段的交界处，如何保证平滑？

所谓平滑，其实就是一阶导数连续，也就是左右导数的极限相同。

对两侧的贝塞尔曲线求导，分别代入 t=0 和 t=1 （即贝塞尔曲线的开始和结束时间），让二者相等。此时能发现，当两侧控制点与分段交接点共线且形成的线段长度相等时，满足曲线平滑性质。

参考资料

B样条曲线

样条曲线

设$[a,b]$为$\mathbb{R}$上的区间
样条是通过一组指定点集而生成平滑曲线的柔性带。 简单地说，B 样条曲线就是通过控制点局部控制形状的曲线。
贝塞尔曲线有以下缺陷：

1. 确定了多边形的顶点数(n+1个)，也就决定了所定义的Bezier曲线的阶次(n次)，这样很不灵活。
2. 当顶点数(n+1)较大时，曲线的次数较高，曲线的导数次数也会较高，因此曲线会出现较多的峰谷值。
3. 贝塞尔曲线无法局部修改。

B样条曲线除了保持Bezier曲线所具有的优点外，还弥补了上述所有的缺陷。
样条曲线的次数是指在指定区间上是几次多项式，阶数是指样条曲线有几阶连续导数。k阶B样条=关于u的k-1次曲线
设有P,P,P,…,P一共n+1个控制点，这些控制点用于定义样条曲线的走向、界限范围，则k阶B样条曲线的定义为:

P ( u ) = [ P 0 P 1 ⋯ P n ] [ B 0 , k ( u ) B 1 , k ( u ) ⋮ B n , k ( u ) ] = ∑ i = 0 n P i B i , k ( u ) P(u)=

= \sum_{i=0}^n P_i B_{i,k}(u) P(u)=[P0​​P1​​⋯​Pn​​]⎣⎢⎢⎢⎡​B0,k​(u)B1,k​(u)⋮Bn,k​(u)​⎦⎥⎥⎥⎤​=i=0∑n​Pi​Bi,k​(u)
式中，$B_{i,k}(u)$是第i个k阶B样条基函数，与控制点$P_i$相对应，u是自变量。
基函数有如下德布尔-考克斯递推式：
B i . k ( u ) = { { 1 , u i ⩽ u < u i + 1 0 , o t h e r k = 1 u − u i u i + k − 1 − u i B i , k − 1 ( u ) + u i + k − u u i + k − u i + 1 B i + 1 , k − 1 ( u ) k ⩾ 2 B_{i.k}(u)=

\begin{cases} \begin{cases} 1,&u_i\leqslant u<u_{i+1}\\ 0,&\rm other \end{cases}" role="presentation">\begin{cases} \begin{cases} 1,&u_i\leqslant u$$\begin{cases} \begin{cases} 1,&u_i\leqslant u&k=1 \\ \dfrac{u-u_i}{u_{i+k-1}-u_i}B_{i,k-1}(u)+\dfrac{u_{i+k}-u}{u_{i+k}-u_{i+1}}B_{i+1,k-1}(u)&k\geqslant 2 \end{cases} Bi.k​(u)=⎩⎪⎪⎨⎪⎪⎧​{1,0,​ui​⩽u<ui+1​other​ui+k−1​−ui​u−ui​​Bi,k−1​(u)+ui+k​−ui+1​ui+k​−u​Bi+1,k−1​(u)​k=1k⩾2​ 约定 0 / 0 = 0 0/0=0 0/0=0，式中 u i u_i ui​是一组被称为节点矢量的非递减序列的连续变化值，首末值一般定义为0和1，该序列如下： [ u 0 , u 1 , ⋯   , u k , u k + 1 , ⋯   , u n , u n + 1 , ⋯   , u n + k ] \left[u_0,u_1,\cdots,u_k,u_{k+1},\cdots,u_n,u_{n+1},\cdots,u_{n+k}\right] [u0​,u1​,⋯,uk​,uk+1​,⋯,un​,un+1​,⋯,un+k​] 相关阅读: 【译】VisualStudio.Extensibility 17.10：用 Diagnostics Explorer 调试您的扩展 命令解压aar、文件压缩成aar图文详解 点赋科技：如何提高淘宝店铺的流量？ 什么是网关？网关有什么作用？ 小程序游戏、App游戏与H5游戏：三种不同的游戏开发与体验方式 IDEA插件Apifox,一键自动生成接口文档！ linux常用服务配置、网络配置 和 基于FTP的上传和下载的几种方式 mysql创建函数实现递归查下级 Linux wait函数用法 进阶JAVA篇-深入了解 Set 系列集合 原文地址：https://blog.csdn.net/wsl_longwudi/article/details/127990837 最新文章 攻防演习之三天拿下官网站群 数据安全治理学习——前期安全规划和安全管理体系建设 企业安全 | 企业内一次钓鱼演练准备过程 内网渗透测试 | Kerberos协议及其部分攻击手法 0day的产生 | 不懂代码的"代码审计" 安装scrcpy-client模块av模块异常，环境问题解决方案 leetcode hot100【LeetCode 279. 完全平方数】java实现 OpenWrt下安装Mosquitto AnatoMask论文汇总 【AI日记】24.11.01 LangChain、openai api和github copilot 热门文章 十款代码表白小特效 一个比一个浪漫 赶紧收藏起来吧！！！ 奉劝各位学弟学妹们，该打造你的技术影响力了！ 五年了，我在 CSDN 的两个一百万。 Java俄罗斯方块，老程序员花了一个周末，连接中学年代！ 面试官都震惊，你这网络基础可以啊！ 你真的会用百度吗？我不信 — 那些不为人知的搜索引擎语法 心情不好的时候，用 Python 画棵樱花树送给自己吧 通宵一晚做出来的一款类似CS的第一人称射击游戏Demo！原来做游戏也不是很难，连憨憨学妹都学会了！ 13 万字 C 语言从入门到精通保姆级教程2021 年版 10行代码集2000张美女图，Python爬虫120例，再上征途 $$