算法day29|491，46，47

491.递增子序列

class Solution:
    def findSubsequences(self, nums: List[int]) -> List[List[int]]:
        used = [False]*len(nums)
        result = []
        nums.sort()
        def backtracking(nums,path,startindex,used):
            nonlocal result
            if len(path)>1:
                result.append(path[:])
            for i in range(startindex,len(nums)):
                if i>0 and nums[i] == nums[i-1] and used[i-1]==False:
                    continue
                else:
                    path.append(nums[i])
                    used[i] = True
                    backtracking(nums,path,i+1,used)
                    path.pop()
                    used[i] = False
        backtracking(nums,[],0,used)
        return result

问题1：如何按照顺序？（一般是直接增序）

class Solution:
    def findSubsequences(self, nums: List[int]) -> List[List[int]]:
        result = []
        def backtracking(nums,path,startindex):
            nonlocal result
            if len(path) > 1:
                result.append(path[:])
            #每进入新的一层循环，都自动清空
            useset = set()
            for i in range(startindex,len(nums)):
                #没有在useset合集中，新加的数要比path里面的最后一个元素大
                #len(path) 防止溢出
                if (len(path)>0 and nums[i]< path[-1]) or (nums[i] in useset):
                    continue
                else:
                    path.append(nums[i])
                    useset.add(nums[i])
                    backtracking(nums,path,i+1)
                    path.pop()     
        backtracking(nums,[],0)
        return result

z代码随想录

重点：不能对集合进行排序，怎么做呢？

任何分析，都需要画个图出来观察

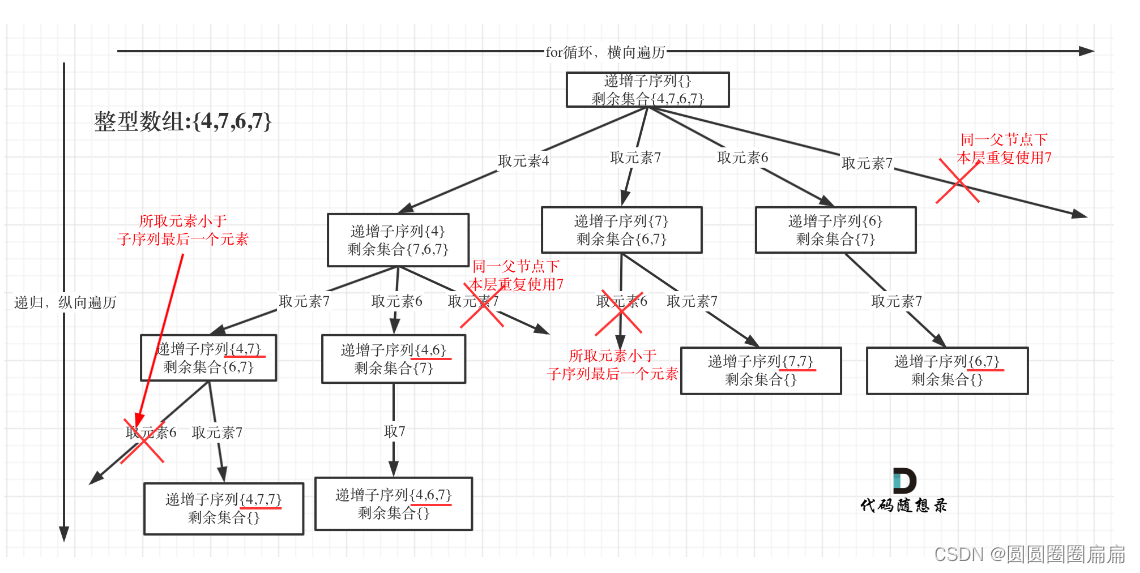
题目要求：

都是递增：所以有个条件就是path中最后一个数要比新加入的数小

删除同一层节点的重复元素？使用一个set存放，如果同一层里面的数存在，就跳过

视频讲解：回溯算法精讲，树层去重与树枝去重 | LeetCode：491.递增子序列_哔哩哔哩_bilibili

二刷（未ac）

var findSubsequences = function(nums) {
    let result = []
    const isValid = function(arr){
        for(let i = 0;i<arr.length-1;i++){
            if(arr[i+1]<arr[i]){
                return false
            }
        }
        return true
    }
    const backtracking = function(nums,path,startindex){
        let used = []
        // when end?
        if(path.length>nums.length){
            return
        }
        if(path.length > 1){
            if(isValid(path)){
                result.push([...path])
            }
        }
        for(let i = startindex;i<nums.length;i++){
            if(used[nums[i]]){
                continue
            }
            used[nums[i]] = true
            path.push(nums[i])
            backtracking(nums,path,i+1)
            path.pop()
        }
    }
    backtracking(nums,[],0)
    return result
};

46.全排列

组合和排列问题差别在：

排列不需要在意集合中的顺序，顺序不同也算不同

组合需要算集合中的顺序，顺序不同不算不同

所以在这里不需要节点去重。

但是需要使用used集合记录一下每个数是否取过 

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        result = []
        used = [False]*len(nums)
        def backtracking(nums,path,used):
            nonlocal result
            #终止条件
            if len(nums) == len(path):
                result.append(path[:])
                return 
            #单层遍历逻辑
            for i in range(0,len(nums)):
                #如果这个数使用过的话，就跳过
                if used[i] == True:
                    continue
                else:
                    path.append(nums[i])
                    used[i] = True
                    backtracking(nums,path,used)
                    path.pop()
                    used[i] = False
        backtracking(nums,[],used)
        return result

代码随想录

视频讲解：组合与排列的区别，回溯算法求解的时候，有何不同？| LeetCode：46.全排列_哔哩哔哩_bilibili
 

二刷（未ac）

var permute = function(nums) {
    let result = []
    let used = new Array(nums.length).fill(0)
    const backtracking = function(nums,path,used){
        // 终止条件
        if(path.length === nums.length){
            result.push([...path])
        }
        for(let i = 0;i<nums.length;i++){
            if(used[i]===1){continue}
            path.push(nums[i])
            used[i] = 1
            backtracking(nums,path,used)
            used[i] = 0
            path.pop()
        }
    }
    backtracking(nums,[],used)
    return result
};

47.全排列 II

本题 就是我们讲过的 40.组合总和II 去重逻辑 和 46.全排列 的结合，可以先自己做一下，然后重点看一下 文章中 我讲的拓展内容。 used[i - 1] == true 也行，used[i - 1] == false 也行

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        result = []
        used = [False]*len(nums)
        nums.sort()
        def backtracking(nums,used,path):
            nonlocal result
            if len(nums) == len(path):
                result.append(path[:])
                return
            #单层逻辑
            for i in range(0,len(nums)):
                if used[i] == True:
                    continue
                elif (i>0 and nums[i] == nums[i-1] and used[i-1] == False):
                    continue
                else:
                    path.append(nums[i])
                    used[i] = True
                    backtracking(nums,used,path)
                    used[i] = False
                    path.pop()
        backtracking(nums,used,[])
        return result

代码随想录

重点：

记得排序啊，重复元素去重，太重要了，这个细节

视频讲解：回溯算法求解全排列，如何去重？| LeetCode：47.全排列 II_哔哩哔哩_bilibili

二刷（ac）

var permuteUnique = function(nums) {
    nums.sort((a,b)=>(a-b))
    let result = []
    let used = new Array(nums.length).fill(0)
    const backtracking = function(nums,path,used){
        if(path.length === nums.length){
            result.push([...path])
            return
        }
        for(let i =0;i<nums.length;i++){
            if(i>0 && nums[i-1]===nums[i]&&used[i-1]===1){
                continue
            }
            if(used[i]===1){
                continue
            }
            path.push(nums[i])
            used[i]=1
            backtracking(nums,path,used)
            used[i]=0
            path.pop()
        }
    }
    backtracking(nums,[],used)
    return result
};