概率论中的几个重要悖论问题

1. 蒙提·霍尔问题（三门问题）

三门问题（Monty Hall problem）亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论，大致出自美国的电视游戏节目Let's Make a Deal。问题名字来自该节目的主持人蒙提·霍尔（Monty Hall）。参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门是否会增加参赛者赢得汽车的机率?

                        

                                                         简单直观的图示解答

 初一看，还以为改选和不改选另外一扇门的几率都是，下面用条件概率来直接计算

a) 坚持原来的选择

        因为汽车的位置是随机放置的，所以获奖几率为 .

b) 换另外一扇门

定义一开始选到汽车为事件,换另外一扇门以后明显不可能获奖了，则.

一开始选到山羊为事件,最终获奖也就是开出的那扇门对应的是汽车为事件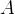，那么获奖的概率可采用全概率公式计算如下

                                        

也就是

                                                

虽然问题就解决了，但还是不知道我们最开始错误的直觉来自哪里。我们来思考一下主持人“提供信息”的问题。一切的改变，都是因为主持人提供给我们的信息：也就是说主持人开的那扇对应山羊的门，提供了额外的信息.因为主持人很明显是知道门背后都是些什么，才打开山羊门的。如果主持人根本就不知道汽车在哪里，只是随手选择了一扇门，而这扇门恰好是山羊门的话，主持人也就是等于没有提供任何信息，这还是原先的随机猜测开门事件。也就是说按主持人的提示更换选择，等价于利用了额外的有效信息,可视为先验信息，这增加了获奖的概率。

2. 犯人的难题

一个监狱里关了三个犯人，已知有两个人即将被释放，但在事情没公布之前，被释放人的身份是保密的.其中一个犯人问看守他的另外两个狱友哪一个被释放。看守拒绝了，他的理由是“在现有的信息下你被释放的概率本来为2/3，如果我告诉了你问的信息，将在你和另外一个犯人之间确定哪一个被释放，那你被释放的概率将变为了1/2，那对你不友好！”，看守所列理由的错误在哪里？

我们看一下这个问题，咋一看很像三门问题，但是它和三门问题有一个决定性的不同！！！三门问题中，抽奖人可以决定要不要更换选择。而在这个问题中，囚犯没有有资格决定释放谁吗？不管看守是否告诉囚犯，都是按既法定程序释放谁，不论他说不说，囚犯也改变不了释放谁的事实，所以从头至尾他被释放的概率都是2/3，详细的计算可先定义如下几个事件.

        事件 A =“A不被释放”，

        事件 B =“B不被释放”，

        事件 C =“C不被释放”，

        事件 W =“看守说B被释放”。

不失一般性，假定上述问看守的是A.

由条件概率公式：

                

我们首先算分母。由全概率公式：

                         

首先，在未揭晓到底谁被释放前，三人不被释放的概率相同，也就是

                                  

事实上如果把全概率公式代入条件概率公式，式子就刚好变成了贝叶斯公式.

表示A不被释放的条件下，看守说B被释放的概率。如果A是不被释放的人，那么看守可以说B将被释放，也可以说C将被释放【注意：A问的是另外两犯人B与C】，因此这个概率是  .

表示B不被释放的条件下，看守说B被释放的概率，这是矛盾的，所以这个概率为0。

表示C不被释放的条件下，看守说B被释放的概率。由于C不被释放，看守在另外的两人中只能说B被释放【注意：A问的是另外两个人谁被释放，不包含A】，因此这个概率是1。

把上面的六个概率代入全概率公式，得

                                                          

同时我们已经求出

                                                 

所以再代入条件概率公式，得

                                         

即看守回答B被释放后，A不被释放的概率还是 [释放的概率为]，而不是，但是C不被释放的概率增加到了还是 

                         

我们回头分析为什么看守（和我们大多数人）的推理是错的，以及这个问题反直觉的地方在哪里。根本原因在于大多数人把事件 W 等同于事件 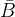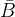（  指的是事件B的对立事件）。

我们首先设定了事件 W =“看守说B不被释放”，事件 B =“B将被释放”，那么事件 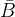=“B不被释放”。

问题的核心在于：“看守说B将不被释放”与“B不被释放”两句话看似一样，其实包含了不同的信息。我们从对立事件的角度就能分析出背后的奥妙。

事件W （即：看守说B被释放）的对立事件是“看守说C被释放”，而事件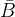（即：B将被释放）的对立事件是“B将不被释放”。两个事件的对立事件是不同的。第一个事件着重回答“谁将被释放”，第二个事件的重点在于“B是否会被释放”。而看守错误地将事件  等同于事件 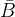，由此他产生了如下推理：

                                                

 （正如之前的分析，这个式子与条件概率公式的区别在于把  都替换成了 ）。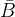

由于  ， 

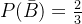所以         P(A|ˉB)=P(A∩ˉB)/P(ˉB)=1/3\2/3=12

错误答案 就是这样产生的。

3.贝特朗悖论

该例子由贝特朗1888年在他的著作《Calcul des probabilités》中提到的一个悖论. 在一给定圆内所有的弦中任选一条弦提出，它说明了这样一个原理：解决一个实际问题时，必须建立无歧义的概率模型.设在一个圆内有一个正三角形，内接于圆周.现在随机的选择一个弦，问其长度大于内接三角形的边长的概率是多少？其回答基于随机选择导致了下图a和图b所示两种互相矛盾的结果.

在图a中，取一个半径，在上随机的选取一个点C，作一条弦垂直于.由初等几何可知，当C点的位置恰好位于的中点时，弦的长度刚好等于内接正三角形的边长，而远离圆心时，弦的长度减小.这样弦的长度大于内接正三角形的边长的概率等于.

在图b中，圆周上取一点V作为顶点.通过V先画出一条切线，然后随机的画出一条通过V的直线.记直线与切线的夹角为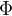，由于这条直线是随机画出来的，可以认为夹角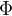在之间是均匀分布的.现在考虑这条直线割圆得到的弦的长度.由初等几何可知，当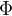位于的范围内，弦的长度大于三角形的边长.由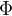于的取值位于，故而可得这个弦大于内接正三角形的概率为.

4. 归纳法悖论

自然归纳法是一种用部分观察定义全体的方法，通过观察到很多某类事物都具有某种性质，那就认为所有该事务具有这样的性质，这增加了对某个命题为真的信心。比如说质量守恒定律，经过大量的观察，而且误差在极小的范围，全体人类最终认定“质量守恒定律”是事实。一个叫亨佩尔的逻辑学家却提出质疑自然归纳法，他提出了如下的所谓归纳法悖论。

现在考虑一个命题，假定 “所有的母牛为白色的” ，其等价的命题为 “凡不是白色的就不是母牛”.当我们观察到几只黑色的乌鸦时候，我们的观察显然与该命题是适应的.但是这些观察会不会使得“所有母牛为白色的”的命题为真的可能性更大一些呢？

为了分析上述问题，我们考虑如下概率模型

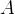                                          ：所有的母牛为白色的

                                         ：50%的母牛为白色的

令表示事件A发生的先验概率，我们分别以  和  观察一头母牛和一只乌鸦.这个观察与A是相互独立的. 假设并且所有乌鸦都是黑色的.

                1) 给定事件B={观察到一只黑色的乌鸦}, 计算

                2) 给定事件C={观察到一头白色的母牛}, 计算

a）计算

        用贝叶斯公式得到：

                                        

因为乌鸦黑不黑和是否看得到白牛没关系，所以，于是.

结论：观察到白牛和所有乌鸦是黑色互相独立，即它们两个没有任何关系。

b)计算

                用贝叶斯公式得到

                                                

通过全概率公式，

        ​​​​​​​        ​​​​​​​        

即：

                        

                        ​​​​​​​

代入得到

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​     

也就是观察到一半黑的才是乌鸦.

注意：整个分析的目的不是为了搞清楚究竟有多少比例的母牛是白色，而是为了说明直觉意义上的“归纳推论方法”是否有效（是否内涵不一致性），结论是“推理方法是有效的”。“观察到一只黑色的乌鸦”并不会对我们判断“所有奶牛都是白色的”命题的真假有所帮助，而“观察到一只白色的奶牛”可以增强我们对“所有奶牛都是白色的”命题为真的“信心”，即后验概率相比先验概率变大了。