Similarity and Matching of Neural Network Representations 论文阅读笔记

这是NIPS2021的一篇论文，文章主要是探究了通过一个stiching layer将两个已训练的不同初始化的相同结构的网络的某一层进行匹配的可能性。

前言

• 作者对 “什么情况下两个表征是相似的？” 提出了一个新的问题：“如果我们知道两个表征是相似的，那么他们以什么方式相似？”为此作者将相似分为了两个方面：“representational similarity”和“functional similarity”
  • representation similarity 即我们常见的距离计算，指直接对两个特征向量计算各种距离
  • functional similarity 指功能相似度，表示两个特征向量被使用的方式的相似性，用于回答这个问题：“网络B能够使用网络A的特征完成其任务吗？”文章主要探讨的就是这个问题。

  这里我想到了一个比较形象的比喻可以用来形容这两个相似度量。想象一个单词“汤勺”，representation similarity比较高的单词可能是“场匀”，而functional similarity比较高的可能是“勺子”。

• 文章做的就是将网络A的激活层特征取出来，加一个仿射变换，送进网络B的同一层。网络B的准确率并没有明显下降。
• 对上述的仿射变换进行研究即可回答“如果我们知道两个表征是相似的，那么他们以什么方式相似？”这个问题。
• 文章发现，两种similarity并不呈明显的正相关关系。当准确率没有明显下降时，两个特征可能具有较低的representation similarity，反之亦然。
• 文章的另一个重要发现是，对特征向量进行奇异值分解得到的主成分并不与信息的内容直接相关。

相关工作

• 下面这篇工作好像也做的是一样的，但是做了不同网络结构的

Yamini Bansal, Preetum Nakkiran, and Boaz Barak. Revisiting model stitching to compare neural
representations. Advances in Neural Information Processing Systems, 35, 2021.

• 此外还有CCA CKA SVCCA PWCCA等工作，衡量相似性

正文

• 如下图所示，其实就是做了这样一件事：把一个网络的某一层特征，接一个stitching layer（文章定义为1x1的卷积），送到另一个网络中去。固定两个网络的参数，只训练stitching layer，看看接起来的网络的准确率如何。而对stitching layer的训练文章介绍了两种方式：task loss matching 和 direct matching
• 

task loss

• 其实就是用model 2 的输出作为soft label，算接起来网络的输出和model的输出的交叉熵，用交叉熵损失去训练stitching layer。也可以直接用 GT 的 label 算交叉熵。实验结果显示两种label训练出来的结果没有差别。

direct matching

• 其实就是直接用 model 2 的特征图 $B\in R^{n\times p}$ 作为target，用 model 1 的特征图 $A\in R^{n\times p}$ 作为input，用最小二乘法找到最优的 $M_0\in C$，使得 $$\Vert A{M}_0-B{\Vert }_F=mi{n}_{M\in C}\Vert AM-B{\Vert }_F$$ 其中 p 为特征图的维度 $p=c$，所以这个其实就是个1x1的卷积，对所有所有图片所有位置的像素都是相同处理，n 为样本数，也可以理解为图像数量乘以hw。
• 考虑C的几种方案：
  • $p\times p$的任意矩阵
  • $p\times p$的满秩矩阵
  • $p\times p$的非满秩矩阵
• 上述三种情况都可以用A的伪逆左乘B矩阵求得近似值，而对于第二和第三种情况，有专门的矩阵算法求得最优解

Sparse matching

• 此外其实还有一种理论是用 ∥ A M 0 − B ∥ F = m i n M ∈ C { ∥ A M − B ∥ F + α ⋅ ∥ M ∥ 1 } \|AM_0-B\|_F = min_{M\in C}\{\|AM-B\|_F+\alpha \cdot \|M\|_1 \} ∥AM0​−B∥F​=minM∈C​{∥AM−B∥F​+α⋅∥M∥1​}作为目标函数，目的是求得一个稀疏的M矩阵，这里的stitching layer的L1范数可以对 direct matching 也可以对 task loss 两种求最优化的方式去添加

实验结果

比较task loss和direct matching

• 
• 如图，可以看到
  • task loss相比direct matching具有更高的准确率（图中用相对准确率来表示迁移模型准确率相比原模型准确率的比值）
  • 不同网络具有不同的匹配相似度，inceptionV1上两个网络的匹配相似度就极高
• 另外，图中没有体现，但论文中提到了两个细节：

  • 有无batch normalization得到的两个网络也可以很好地用上述两个方法匹配；不同optimizer优化的模型也可以；

  • 用direct matching先初始化参数后再用task loss去训练可以得到稳定且较高准确率的训练结果；而随机初始化则随着研究层的变浅逐渐呈现不稳定的结果。
    

  • 即使是用不同训练集训练的两个模型，仍然能很好地配对

比较不同width

• 
• 作者将 Resnet 的被匹配层的通道数分别增加为原来的2 3 4倍，再用 task loss 去训练，发现accurcay增加了不少

representation similarity不同于functional similarity

• 作者观察了在task loss训练过程中，基于特征之间距离计算的相似性度量指标的变化情况，如下图所示
  
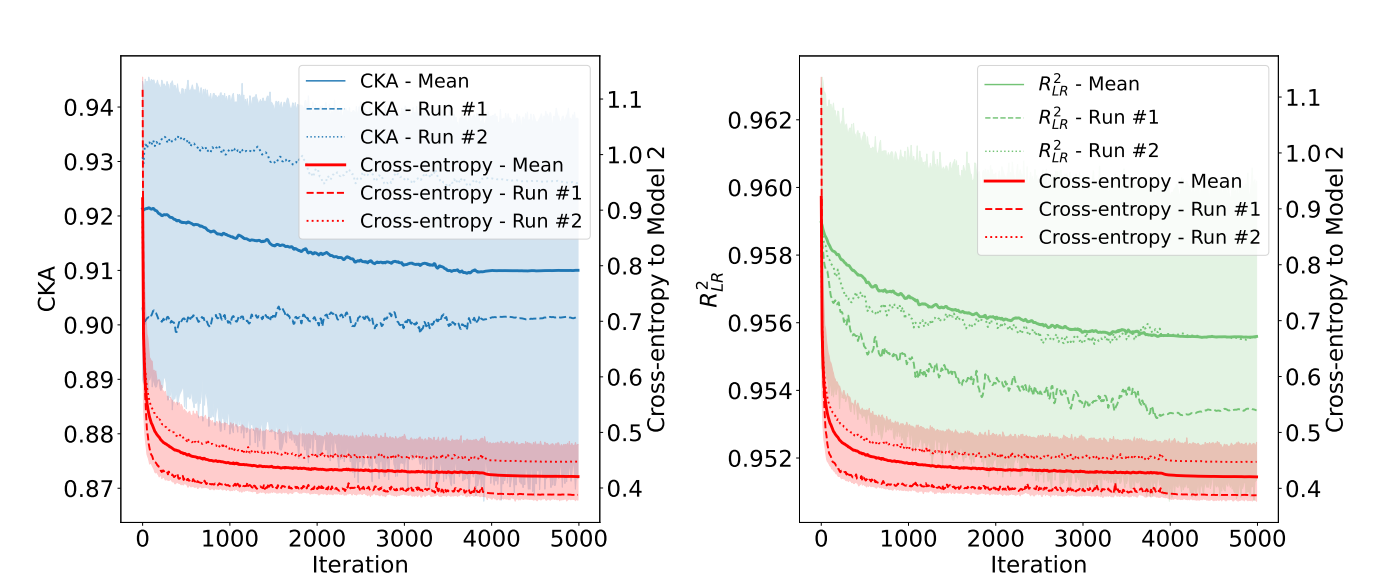
• 可以看到，随着训练的迭代，交叉熵降低，因此模型准确率提高，functional similarity因此提高，但很明显基于特征距离函数的相似性度量指标CKA和R2在多次训练中呈现出方差大、总体呈下降趋势的现象。
• R2相似度的下降是显然的，因为 sitiching layer 是 direct matching 进行初始化的，因此0迭代处即为R2相似度的最大值。但这也说明了，基于最小二乘的 direct match得到 的stitching layer 显然并不体现模型的决策边界，也并非 functional similarity 最高的结果。
• 作者还做了另一个有趣的实验，将模型A对自身进行match，将 stitching layer 初始化为单位矩阵，因此相似性度量一开始就是最大值。然后训练 stitching layer，除了原先的task loss，还增加了相似性度量（可导）作为损失，因此一边训练，stitching layer产生的特征图与原特征图的相似度就会不断下降，但实验结果显示与此同时交叉熵并没有显著增加，准确率也没有显著下降。因此可以说明，基于距离计算的 representation similarity，并不是 functional similarity的必要条件。
  

低秩实验

• 前面说了，stitching layer可以是不满秩的，不满秩的网络可以通过 bottleneck 结构（即通道数先减小再增加，其实就是把 $p\times p$ 的矩阵分解为 $p\times k$ 的矩阵和 $k\times p$ 的矩阵的乘积，从而使得乘积的秩最多为k，可以通过SVD分解来实现）的模块来实现。
  
• 在不满秩的情况下实验可以发现，task loss仍然得到了最优的准确率，这进一步验证了前面的结论。

对stitching layer的性质探究

• 通过不同初始化得到的stitching layer，除了部分陷入了局部极小值而导致准确率下降很大之外，其它的基本都能收敛到相近的准确率附近
• 并且，这些表现很好的stitiching layer，呈现出了连续性，取两个不同的stitching layer，在两者之间进行插值，插值得到的一系列stitiching layer仍然具有很高的准确率。

稀疏的stitching layer

• 通过添加stitiching layer 的L1范数作为损失，并且在训练结束后将低于阈值的参数置为零从而实现稀疏的stitching layer。在稀疏的stitching layer上得到的准确率实验结果如下：
  
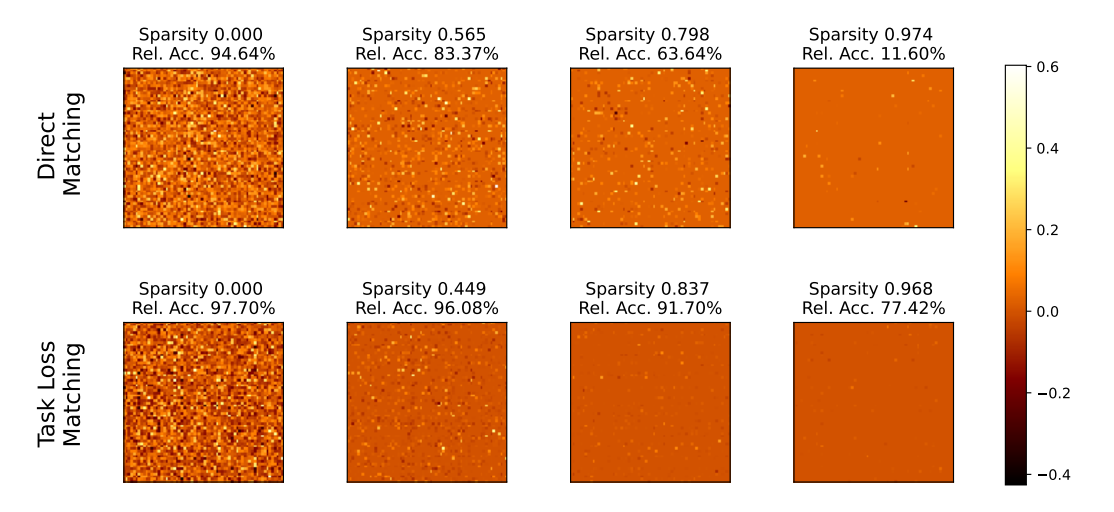
• 可以看到，随着稀疏系数（零参数占参数总量的百分比）的提高，基于task loss的stitching layer准确率下降并不明显，仍然可以接受；而基于direct matching的则出现了严重的下降。