-
基于特征选择的二元蜻蜓算法(Matlab代码实现)
🍒🍒🍒欢迎关注🌈🌈🌈
📝个人主页:我爱Matlab
👍点赞➕评论➕收藏 == 养成习惯(一键三连)🌻🌻🌻🍌希望大家多多支持🍓~一起加油 🤗
💬语录:将来的我一定会感谢现在奋斗的自己!
🍁🥬🕒摘要🕒🥬🍁
特征选择是模式识别的关键问题之一,特征选择结果的好坏直接影响着分类器的分类精度和泛化性能。
蜻蜓算法(DA)是一种通过模拟自然界中蜻蜓种群觅食和迁徙行为而设计的求解全局优化问题的新型元启发算法,具有实现简单、调优参数少、收敛时间短等特点,广泛应用于各领域优化不同问题。本文根据DA易过早收敛的缺点,分别从增加改进策略和混合其他搜索算法的角度给出解决方法。
✨🔎⚡运行结果⚡🔎✨
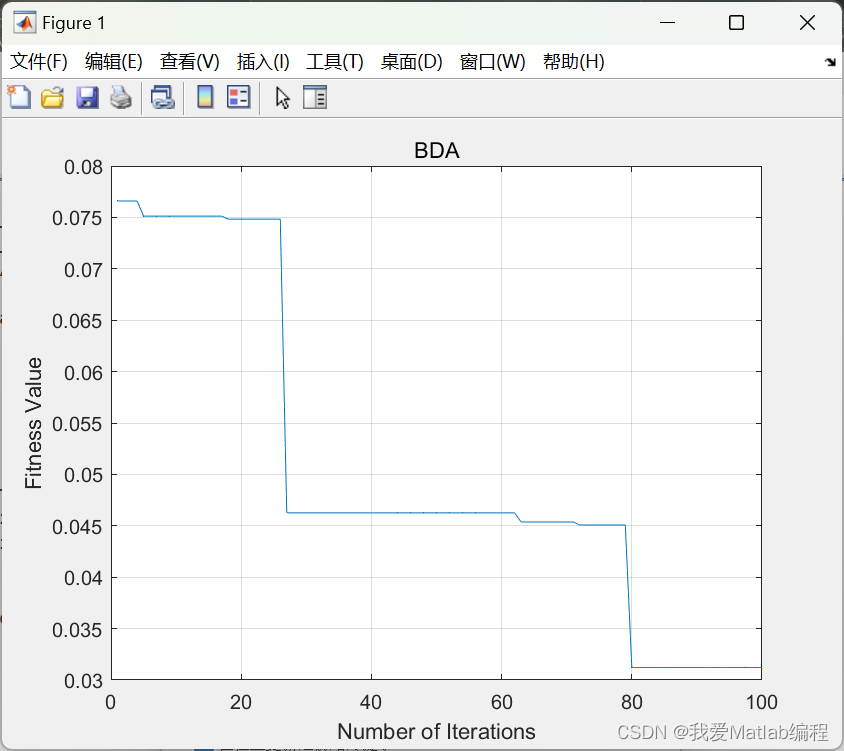
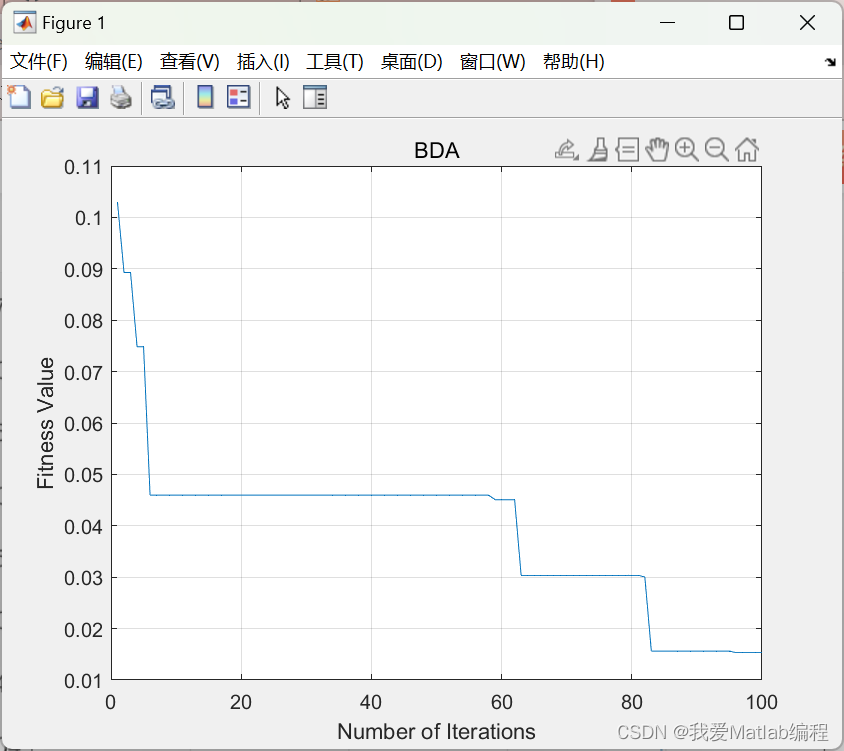
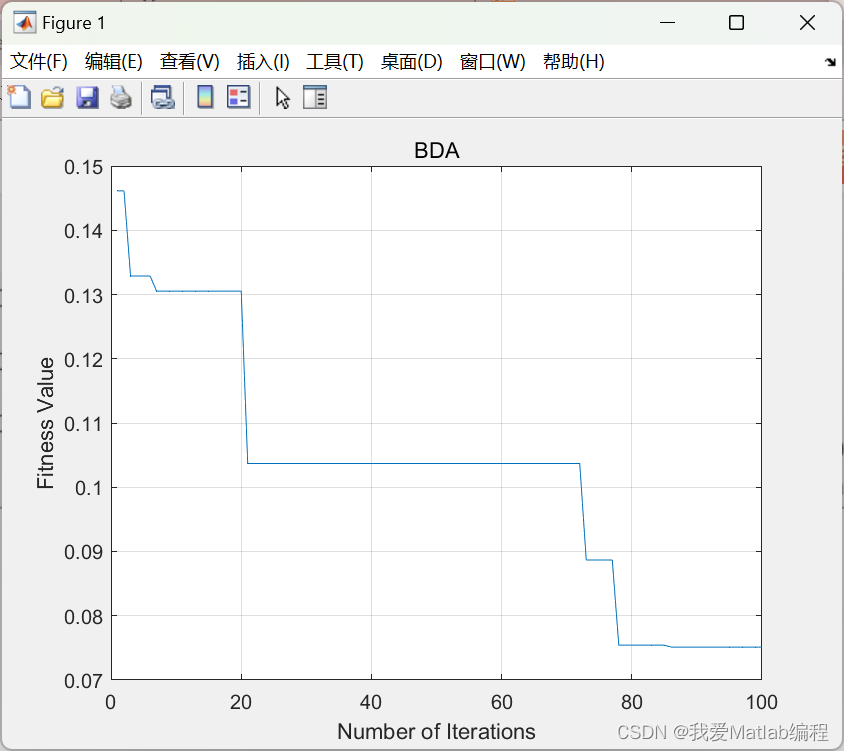
💂♨️👨🎓Matlab代码👨🎓♨️💂
%-------------------------------------------------------------------%
% Binary Dragonfly Algorithm (BDA) demo version %
%-------------------------------------------------------------------%
%---Inputs-----------------------------------------------------------
% feat : feature vector (instances x features)
% label : label vector (instances x 1)
% N : Number of dragonflies
% max_Iter : Maximum number of iterations%---Outputs-----------------------------------------------------------
% sFeat : Selected features
% Sf : Selected feature index
% Nf : Number of selected features
% curve : Convergence curve
%---------------------------------------------------------------------
%% Binary Dragonfly Algorithm
clc; clear; close
% Benchmark data set
load ionosphere.mat;% Set 20% data as validation set
ho = 0.2;
% Hold-out method
HO = cvpartition(label,'HoldOut',ho,'Stratify',false);% Parameter setting
N = 10;
max_Iter = 100;
% Perform feature selection
[sFeat,Sf,Nf,curve] = jBDA(feat,label,N,max_Iter,HO);% Accuracy
Acc = jKNN(sFeat,label,HO);% Plot convergence curve
plot(1:max_Iter,curve);
xlabel('Number of Iterations');
ylabel('Fitness Value');
title('BDA'); grid on;📜📢🌈参考文献🌈📢📜
[1]池建华,蔡延光,李俊奕,李立欣,陈子恒,苏锦明.蜻蜓算法研究综述[J].自动化与信息工程,2022,43(03):7-14.
-
相关阅读:
Kali实现ARP欺骗
换天空背景的软件有哪些?什么软件可以一键换背景?
深度ESP32 PWM教程如何在ESP32 中使用PWM
科目三基础四项(一)
MindSpore:一文带你入门虚拟遗憾最小化CFR算法
企业应用架构研究系列二十七:Vue3.0 之环境的搭建与Vue Antd Admin探索
JavaScript:从入门到进阶的旅程
信息学奥赛一本通题解目录(没写完)
【Python】深入理解NumPy数组中的一维向量
jQuery常用API--样式操作
- 原文地址:https://blog.csdn.net/m0_73907476/article/details/127966790