数字信号处理-2-三角函数与谱

1 弧度的定义

为了便于数学上的运算，设以半径为 1 的圆的中心为原点，x 轴正方向为基准测量角度。这样的圆为单位圆，此单位圆的长度为 1，在圆周上取与半径相同长度的圆弧，对应的角度为 1 弧度。

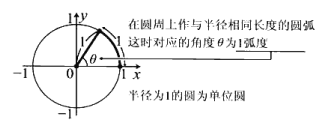
更确切地说，弧度是角度对应的圆弧与半径的比值 $\theta (弧度)=l/R$

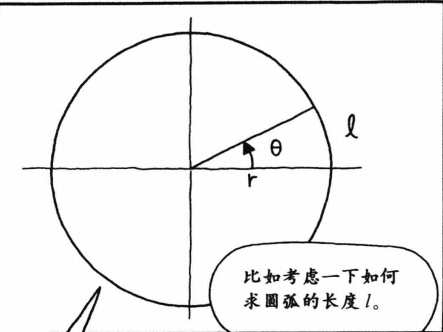
在三角函数中弧度能大大地简化运算

如计算圆弧长度：
圆弧的长度 $l=\theta \ast R$ 就避免了π 的出现

$扇形面积=（\theta /2\pi ）\ast \pi \ast r^2=(1/2)\ast \theta \ast r^2=(1/2)lr$

弧度与角度对应关系

2 旋转与三角函数

现在有一个单位圆，半径为 1，旋转角度为 θ，则它在 y 轴上的投影为 1sinθ,在 x 轴上的投影为 1cosθ。

可以把此单位圆想象为摩天轮，摩天轮的高度随着转动角度的变化而变化

对应到波形图中（下面左图），横轴为旋转角度，纵轴为高度，这个图形就是正弦函数。纵轴值 y 是横轴（角度）值 x 的函数。正弦函数与旋转运动就联系起来了，单位圆上旋转角度 θ 一圈一圈的变化（下面右图），表现在波形图中（下面左图）就是随着 θ 的变化，y 值呈现周期性的变化

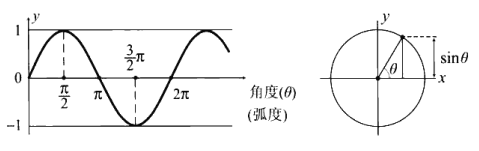
同理，如果纵轴表示的是在 x 上的投影，则这样的图形就是余弦函数。

将 sinθ 与 cosθ 画到一起可以看出，cosθ 只是滞后了 sinθ 的 π/2。将 cosθ 向右水平移动 π/2 后两者图形相同。

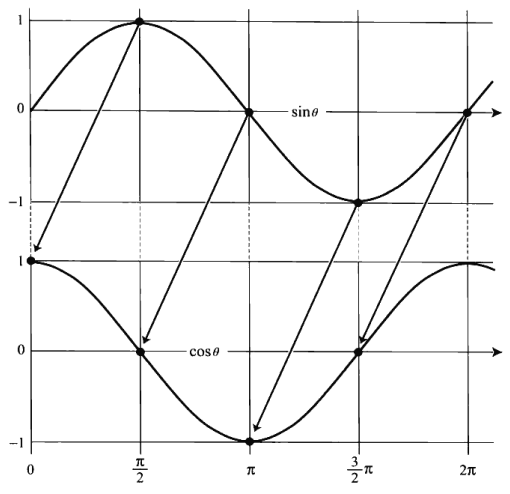
3 ωt 与三角函数

在三角函数中，变量是 θ，表示旋转角度。

在物理学中，物理量 ω 叫做角速度，单位是弧度/秒(rad/s)，角速度可以用快慢来形容。ω (rad/s)乘以时间 t(s)得到的物理量就是角度了。ω 也叫做角频率，角频率与频率有很大的联系。

物质在单位时间内完成周期性变化的次数叫做频率，常用f表示，单位为Hz。

假设周期为 T，频率 f 为周的倒数
$$f=1/T$$
完成一周转动需要时间 T，转动的弧度为 2π，所以
$$\omega =2\pi /T$$
将 f 带入就有：
$$\omega =2\pi f$$
所以角频率 ω 是频率的 2π 常数倍

3.1 单个 ω 图形

假设 ω 确定，那么三角函数就可以表示为与时间相关的函数了，
sinθ = sinωt

ω 与 r(半径) 值都固定，用图形表示就是下图，它不随时间变化，是一种静态图形

3.2 多个 ω 图形

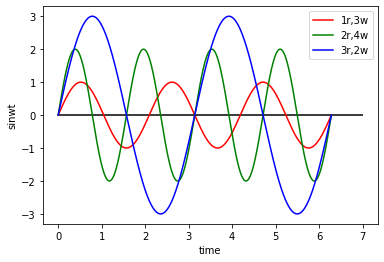
现在假设我们有三个 ω，这三个 ω 固定。分别表示慢速、正常速和快速。它们的半径分别是 1、2、3，角速度 ω 分别是 3ω、4ω、2ω

下图表示波形随时间变化(代码见第 5 部分)

ω 与 r 均已知且固定，ω 表示为横轴，r 表示为纵轴，就可以得到下面的图形

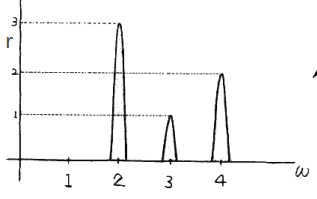
这也就是谱的图形，当然这里横轴是角频率，也可以换成频率

4 三角函数公式

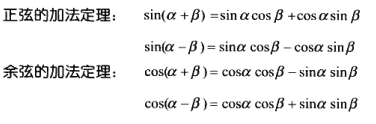
5 Python 代码

# jupyter noteboook 中运行
# 导入需要的包
import numpy as np
from matplotlib import pyplot as plt

# 常数值 2π
PI2 = math.pi * 2
framerate = 22050
n = 22050
# 2*PI2 平均分为 10000 份
ts = np.linspace(0, PI2, 10000)
# r1,2,3  w3,4,2
w = 1

r1 = 1
w1 = 3*w

r2 = 2
w2 = 4*w

r3 = 3
w3 = 2*w

ys1 = r1 * np.sin(w1*ts)
ys2 = r2 * np.sin(w2*ts)
ys3 = r3 * np.sin(w3*ts)

plt.plot(ts,ys1,'r',label='1r,3w')
plt.plot(ts,ys2,'g',label='2r,4w')
plt.plot(ts,ys3,'b',label='3r,2w')
plt.hlines(0, 0, 7)#横线
# 给图片在右上角添加图例
plt.legend()
plt.xlabel("time")
plt.ylabel("sinwt")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

参考

漫画傅里叶解析
Python数字信号处理应用
角频率和频率的关系