前缀和【一维前缀和与二维前缀和】

全文目录

• 😀 一维前缀和
• • 🤔 构建一维前缀和数组
  • 😵‍💫 子序列的和
• 😀 二维前缀和
• • 🤔 构建二维前缀和数组
  • 😵‍💫 子矩阵的和

😀 一维前缀和

一维前缀和很简单，就是高中数学中的前n项和。

设有一个数组a[]：

a = {a[1], a[2], a[3], a[4], a[5], a[6], ... , a[n]};
1

还有一个数组 S[]：

S = {S[1], S[2], S[3], S[4], S[5], S[6], ... , S[n]};
S[1] = a[1];
S[2] = a[1] + a[2];
S[3] = a[1] + a[2] + a[3];
S[4] = a[1] + a[2] + a[3] + a[4];
...
S[n] = a[1] + a[2] + a[3] + a[4] + ... + a[n];
1
2
3
4
5
6
7

那么就称 S[] 为 a[] 的前缀和数组。我们可以利用前缀和数组快速求出原数组中一段区域内的总和

---

🤔 构建一维前缀和数组

小技巧：

数组的下标是从 0 开始的，我们可以多开一个空间，让a[]的下标从 1 开始。
在构建前缀和数组时，可以将多开一个空间，将S[0] 初始化为0，并从S[1] 开始构建，这样就可以让前缀和数组中的全部元素都使用同一公式来构建。

// n表示数据个数
// 下标从1开始，S[0] = 0; 
for (int i = 1; i <= n; i++)
{
	S[i] = S[i - 1] + a[i];
}
1
2
3
4
5
6

---

😵‍💫 子序列的和

我们可以用前缀和数组来求原数组中 [l, r] 的和

a[l] + ... + a[r] = S[r] - S[l - 1]

根据公式推导一下：
S[r] = a[1] + a[2] + a[3] + ... + a[r]
S[l - 1] = a[1] + a[2] + a[3] + ... + a[l - 1]
S[r] - S[l - 1] = a[l] + a[l + 1] + ... + a[r]
1
2
3
4
5
6

---

😀 二维前缀和

如果说一维前缀和是线性的，那么二维前缀和就是平面的。

---

🤔 构建二维前缀和数组

为了方便构造前缀和数组，数组的下标都从1开始。

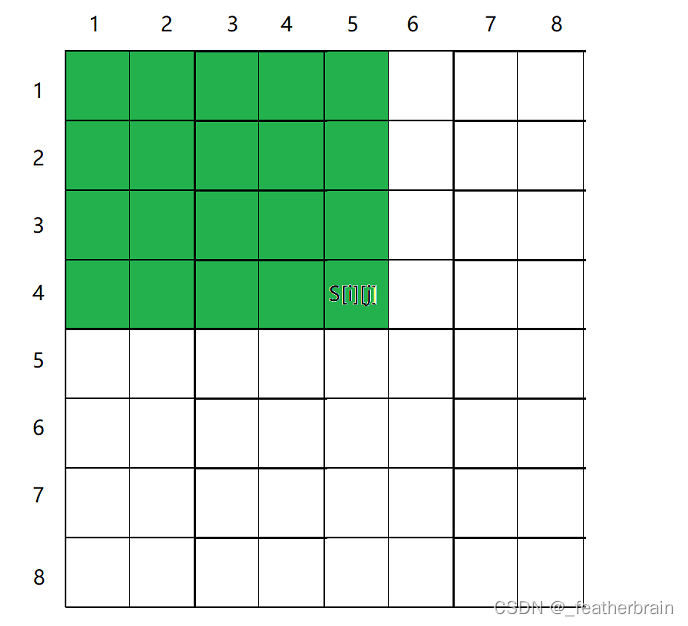
二维前缀和数组S[i][j] 是原数组中左上角的和：

拿 S[4][3] 为例：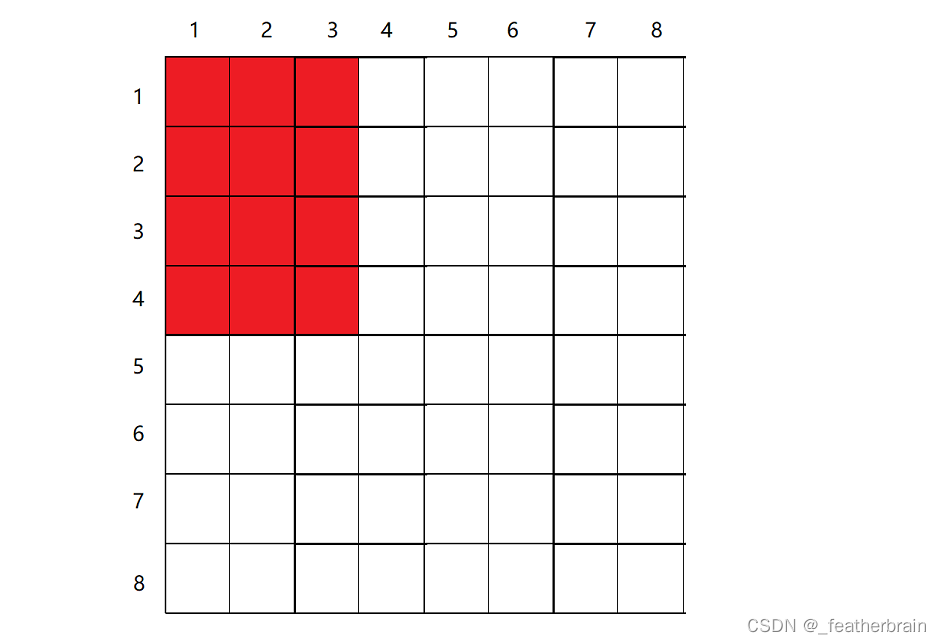

S[4][3] 就是原数组中红色区域的和。

公式：
将a[i][j] 左边的数据和上边的数据加上，再将都加的数据减去一份，在加上 a[i][j]

S[i, j] = S[i, j - 1] + S[i - 1, j] - S[i - 1, j - 1] + a[i, j]
1

根据画图来感受一下构建过程：

先将左边的数据加上，S[i, j - 1] ：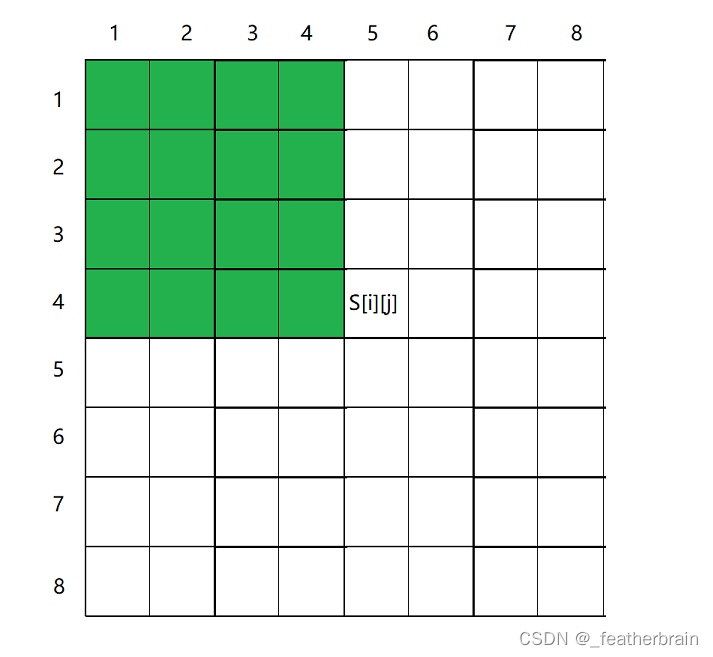

然后将上边的数据加上，S[i, j - 1] + S[i - 1, j]：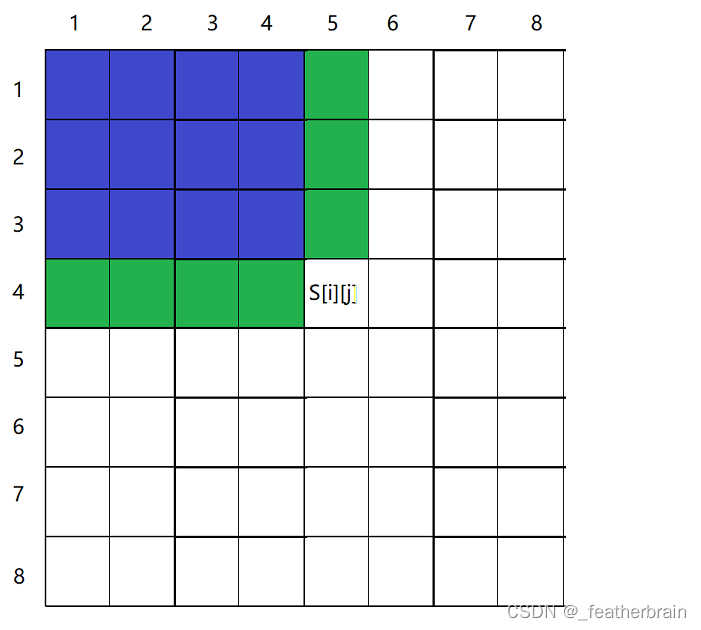

因为S[i - 1][j - 1] 被加了两次，所以需要 减去一份S[i - 1][j - 1].

将多加的数据减去，S[i, j - 1] + S[i - 1, j] - S[i - 1][j - 1]：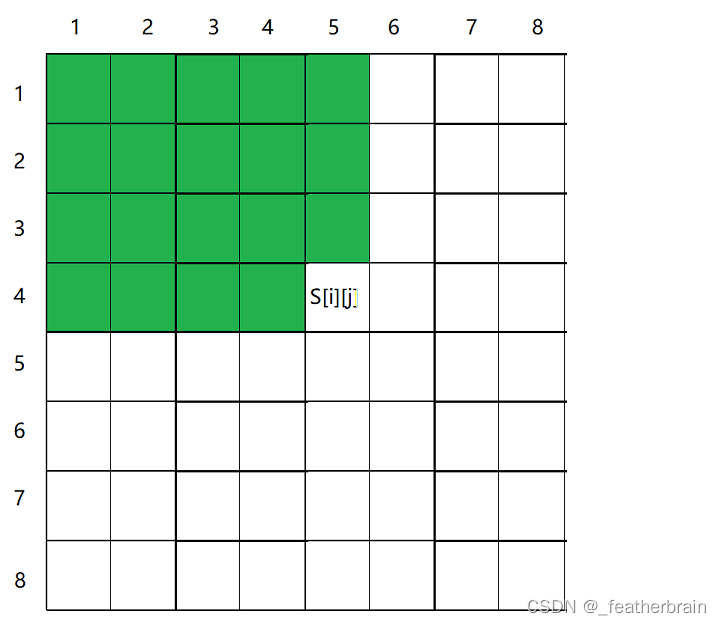

最后将 a[i][j] 加上，就是S[i][j]:

S[i, j] = S[i, j - 1] + S[i - 1, j] - S[i - 1, j - 1] + a[i, j]

---

😵‍💫 子矩阵的和

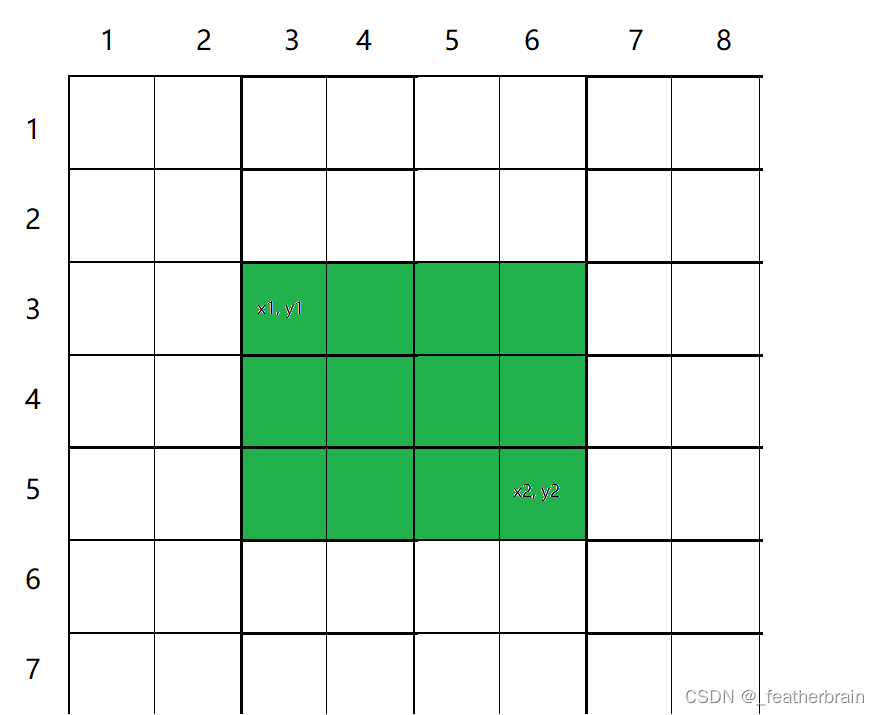
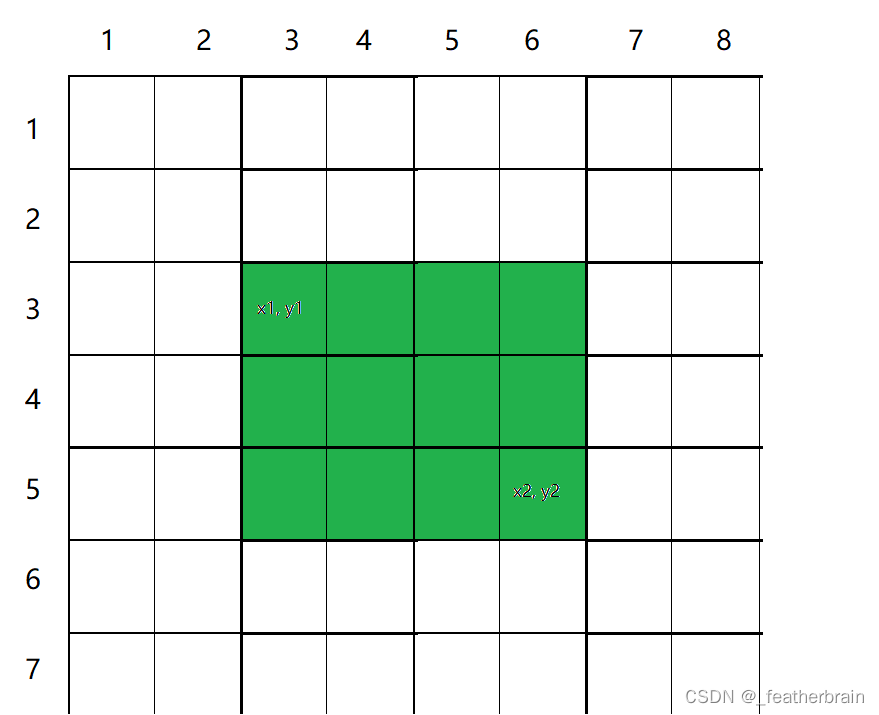
二维前缀和一般用来求子矩阵的和，子矩阵以 (x1, y1) 为左上角，(x2, y2) 为右下角：

公式：
子矩阵的和跟构建二维前缀和数组时的公式很像，将多余的减去，再将多减的加上

子矩阵的和 
= 
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
1
2
3

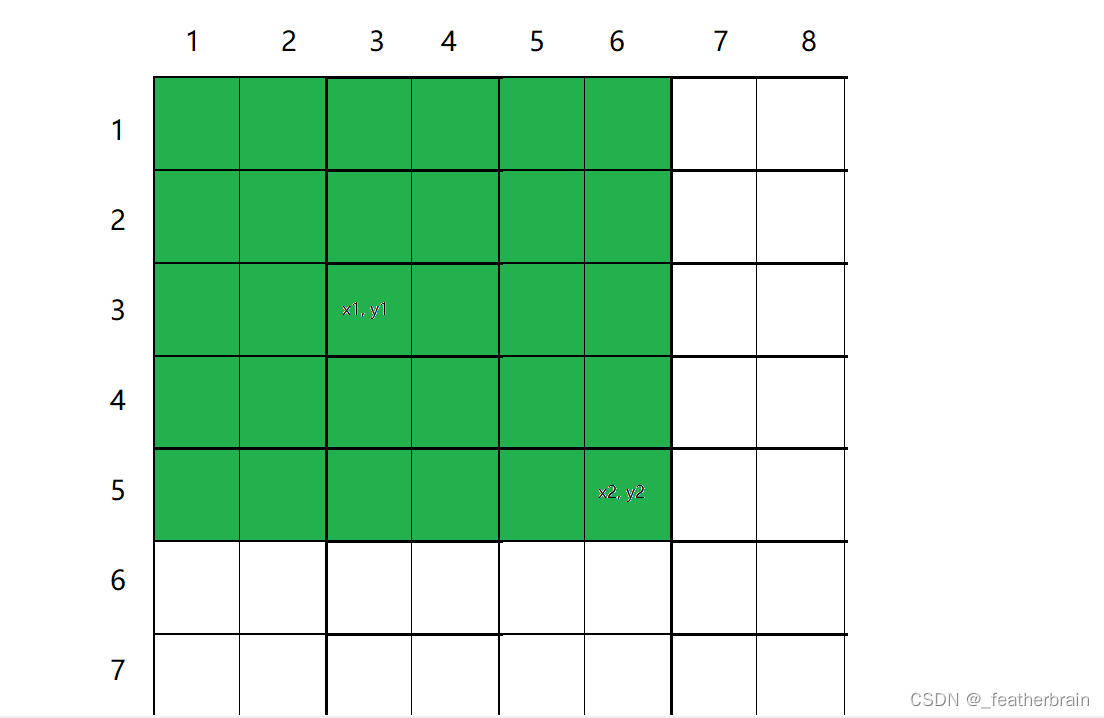
同样的画图来感受一下：

S[x2,y2]:

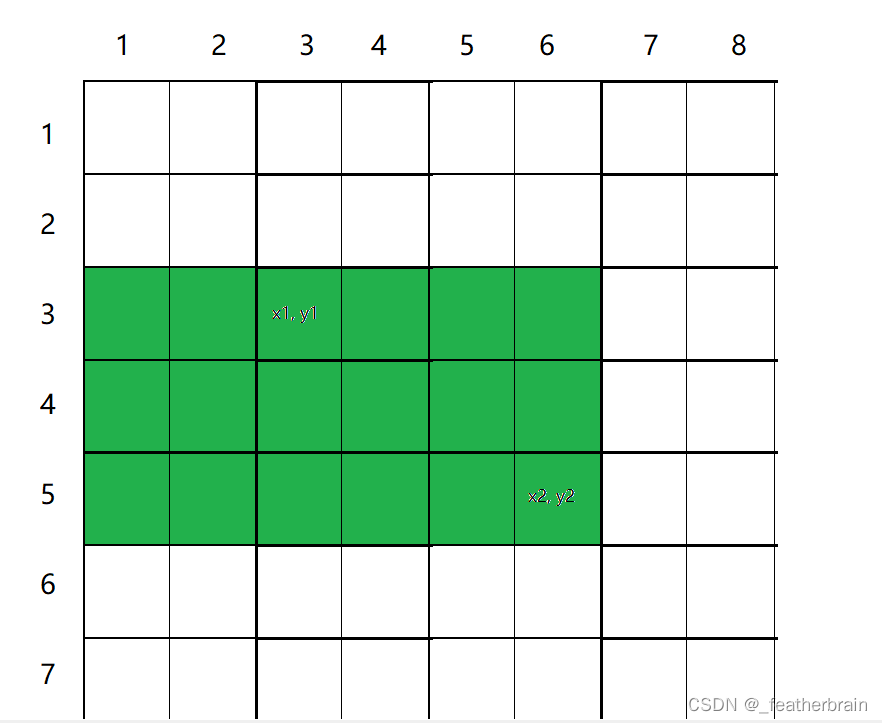
减去子矩阵上边的数据，S[x2, y2] - S[x1 - 1, y2]：

减去子矩阵左边的数据，S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1]：

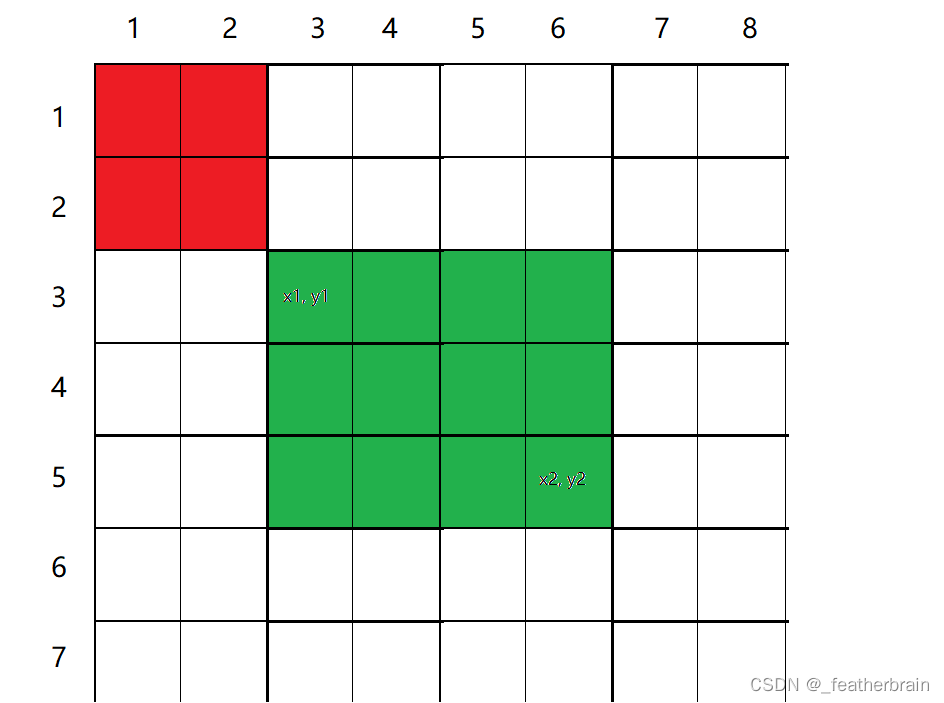
S[x1 - 1][y1 - 1] 被减去了两次，所以需要将这块区域补上，
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]：

---

完结散花🌈🌈🌈