【三维点云】2-三维点云表征

内容概要

1 三维数据的获取方式
2 三维数据的获取原理
3 三维信息的表征形式
4 深度学习中的三维表征
5 点云的基本特征和描述
6 三维空间变换

1 三维数据的获取方式及原理

1.1 被动测量

单目立体视觉

双目立体视觉

多目立体视觉

1.2 主动测量

结构光3D成像

TOF 3D成像

脉冲法

TOF

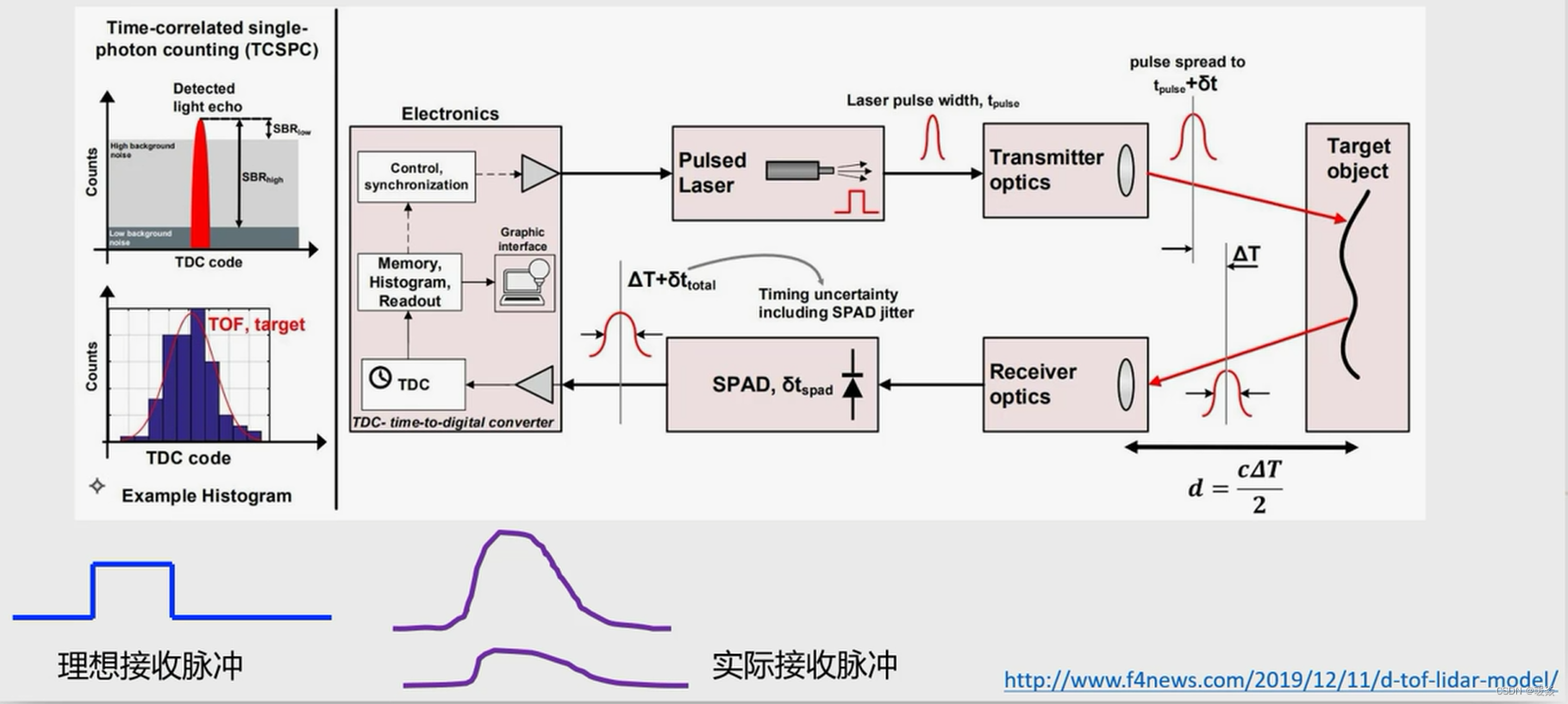
精确测量上升沿时间差受到距离、接收脉冲失真等影响。

相位法

2 三维数据的获取原理

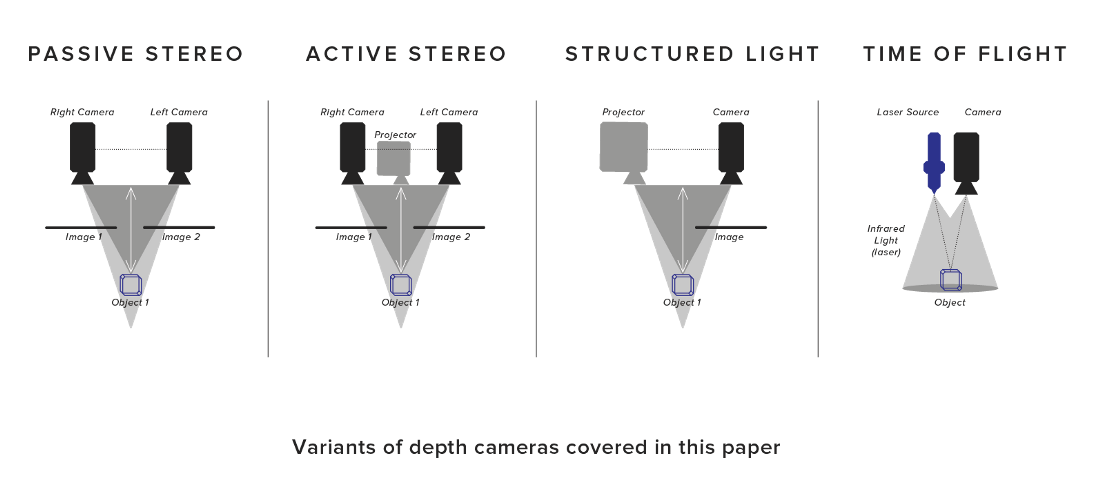
RGBD

立体视觉测量法

相机成像模型

小孔成像模型（相机成像模型的理想情况）

小孔成像中没有畸变，但是在相机成像中，可能出现光心偏移或者透镜材质不均匀导致的畸变。

单目立体视觉

聚焦法

相机主动调焦，并使相机相对于被测点处于聚焦位置，然后根据透镜成像公式求得被测点相对于相机的距离。相机偏离聚焦位置会带来测量误差，因此寻求精确的聚焦位置是关键所在。

离焦法

不要求相机相对于被测点处于聚焦位置，而是根据标定出的离焦模型计算被测点相对于相机的距离，这样就避免了由于寻求精确的聚焦位置而降低测量效率的问题，但离焦模型的准确标定是该方法的主要难点。

单目棱镜法（变向实现多目）

主要应用于微观结果或光学研究。

双目立体视觉

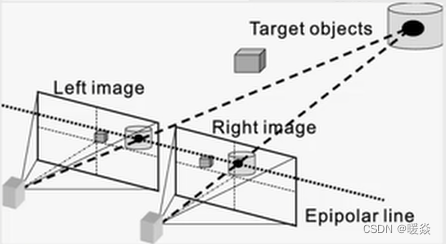
双目视觉是利用视差原理计算深度。两幅图片因为相机视角不同带来的图像的差别构成视差。

1、首先需要对双目相机进行标定得到两个相机的内外参数、单应矩阵（一张图像到另一张图像的转换矩阵）。
2、根据标定结果对原始图像校正，校正后的两张图像位于同一平面且互相平行。
3、对校正后的两张图像根据极线约束进行像素点匹配。
4、根据匹配结果计算每个像素的深度，从而获得深度图。

理想情况

非理想情况

案例

图像矫正和极线约束后，两张图像中的相同物体会在一个高度，通过左图中的坐标位置，在右图中窗口搜索相同坐标位置前后寻找差异最小的窗口。


公式中d是视差。

深度越大，角度越小，视差越小。

窗口越大，深度图越模糊。

如何评价双目视觉？

对边界处深度的估计，无纹理地方的估计，渐变面的深度估计，遮掩地方的估计，还有计算的时间，内存。

主动双目视觉

利用投影在物体上的图案，帮助两个相机计算双目匹配。有多种可能的投影图案，一个方案是使用伪随机散斑。

主动双目视觉测量法与结构光测量法没有明显的界定，主动双目视觉测量法有两个相机，结构光测量法只用一个相机。

结构光3D成像法

上图左上角图中为什么不使用TOF测量法？
距离很近的情况下，如果使用TOF测量法对芯片的精确度要求很高。

点结构光

使用单个点结构光 (e.g.激光点)扫描整个对象。传感器检测物体反射的结构光，使用三角测量法，计算从物体到扫描仪的距离。

线结构光

使用三角测量法，利用投影仪在物体投射一系列结构化线束。通过检测光线的边缘，计算出从扫描仪到物体表面的距离。

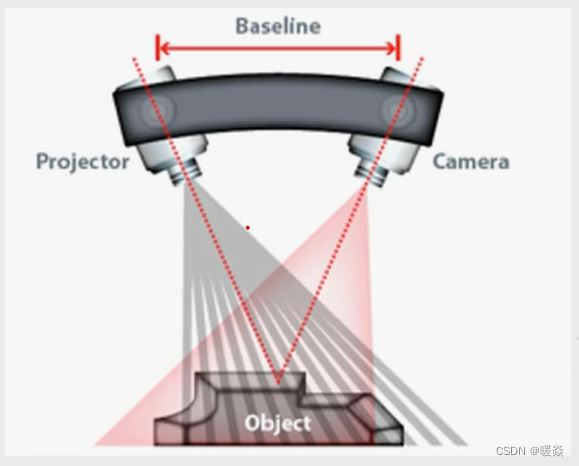
面结构光

投影面结构光到物体表面，需要对面结构光进行编码，知道每个面结构光中的点与所成像中像素的对应关系，然后进行计算。

如何设计结构光的结构？

直接编码，时分复用，空分复用

直接编码

时分复用

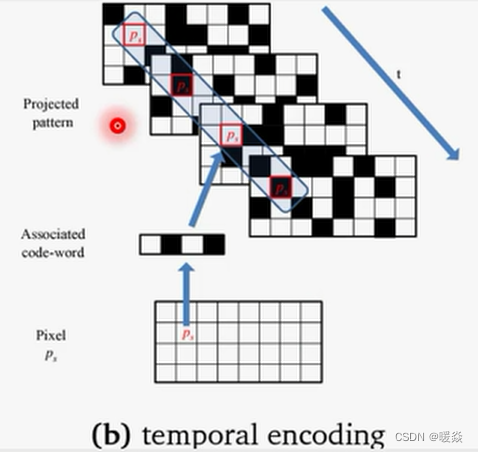
空分复用

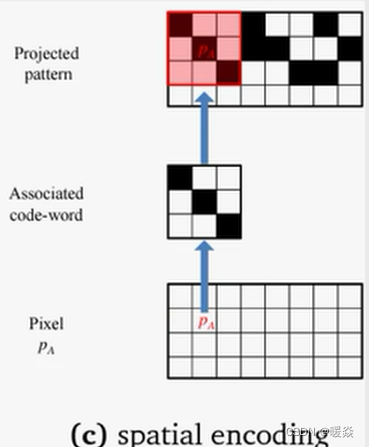
核心问题：散斑结构必须不重复。

如何设计不重复的散斑结构？
栅格化得到bitsmap

多目立体视觉

机器人系统里应用的多。

3 三维信息的表征形式

图片来源 http://graphics.stanford.edu/courses/cs468-17-spring/

点云 PointCloud

参数化曲线曲面 Parametric Surface

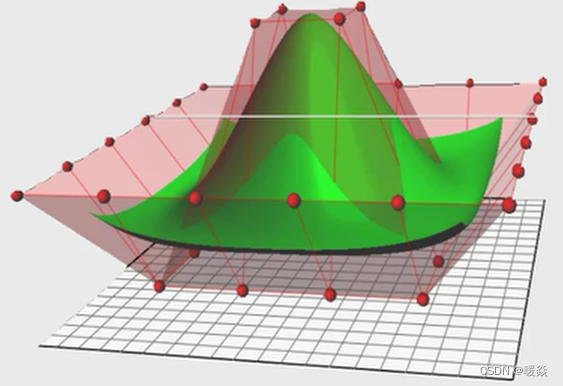
参数化曲线

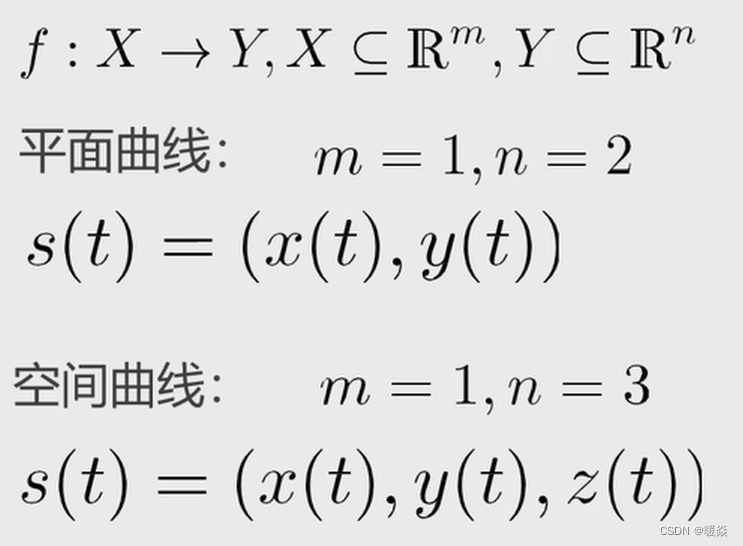
常用参数化曲线

贝塞尔曲线（应用：样条线）

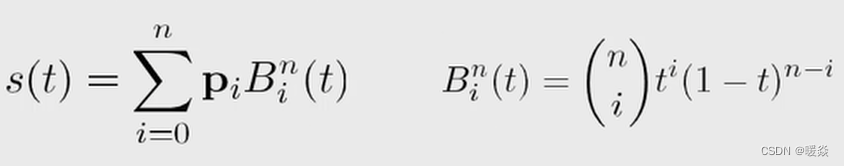
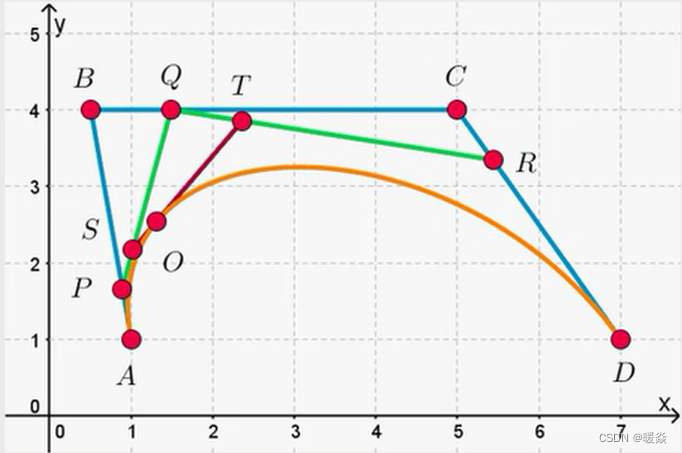
参数化曲面

参数化曲面表示

优点

容易生成曲线或者曲面上的点
参数分离，容易分析

缺点

难以确定内部外部空间
难以判断点是否在曲面曲线上
难以生成非常复杂的曲线曲面（解决：局部表面（多边形面元））

常见的参数化曲面

曲线扫描得到曲面

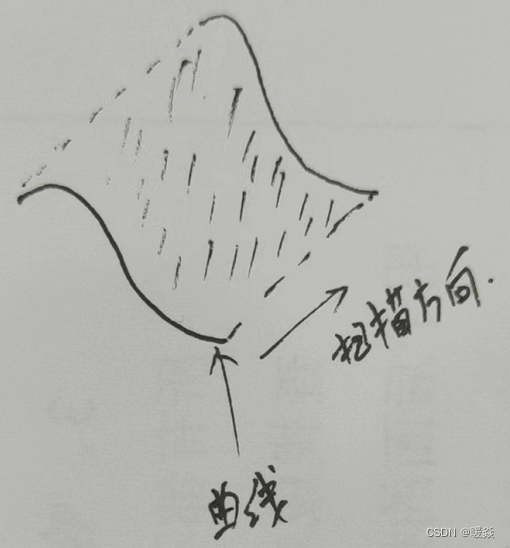
贝塞尔曲面

隐式曲线曲面 Implicit Surface

隐式曲面表示

优点

容易确定内部外部空间。
容易确定点是否在曲线曲面上。

缺点

难以生成曲线曲面上的点。
不适合实时渲染。

常见隐式曲面

图片来源：https://virtualmathmuseum.org/Surface/gallery_o.html

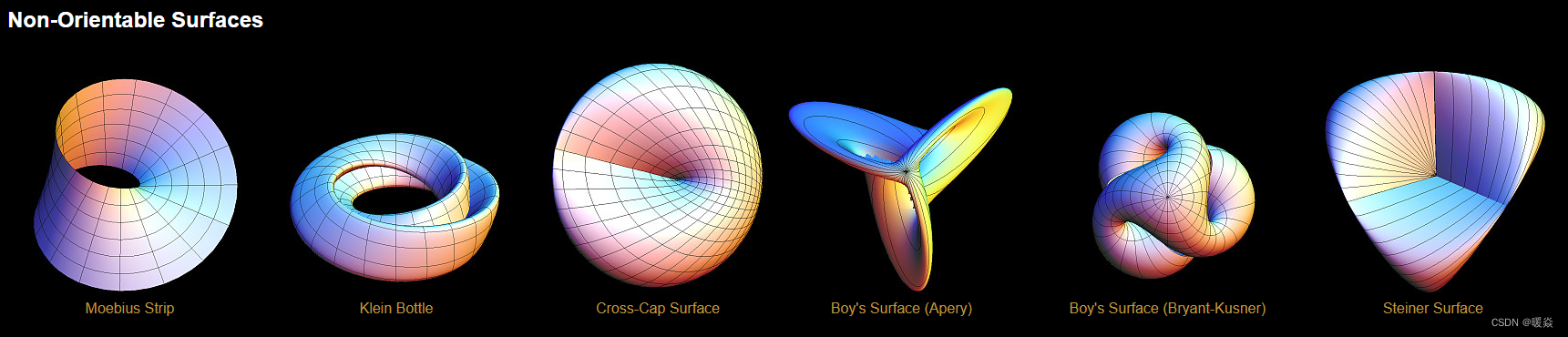
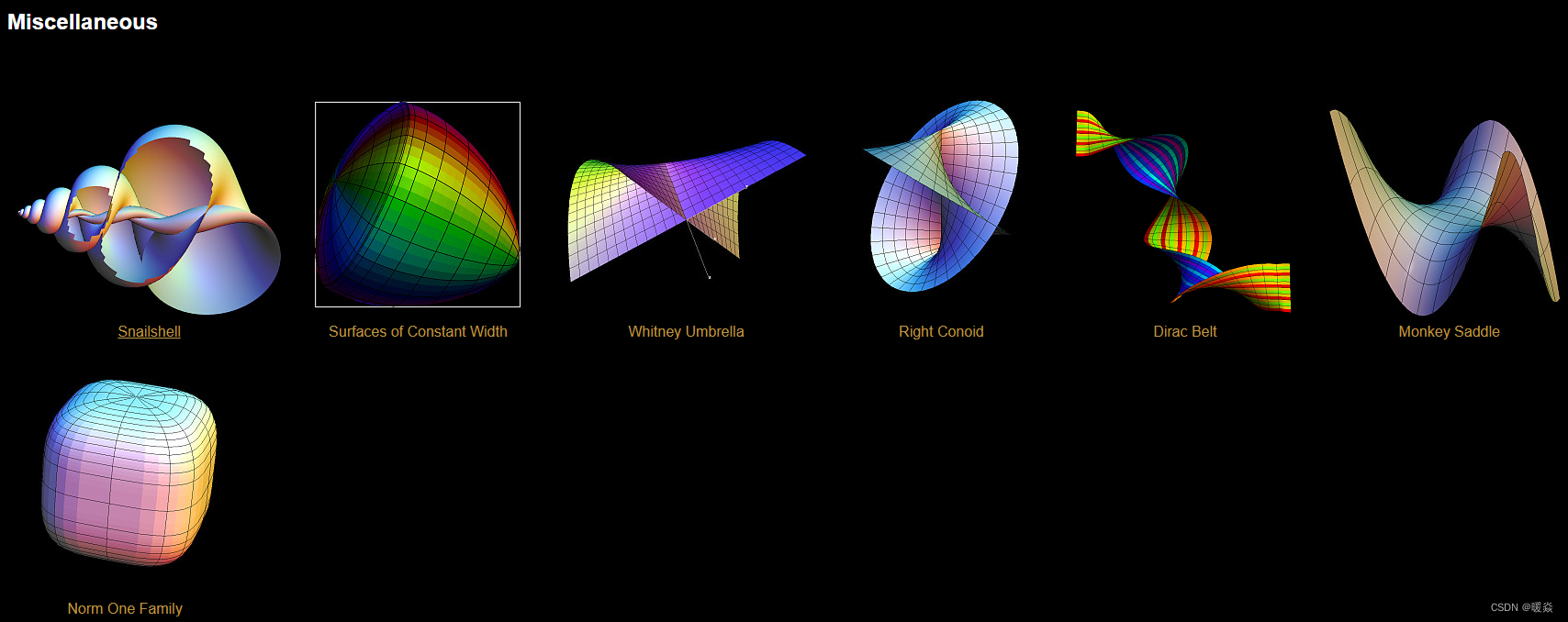
细分曲面 Subdivision Surface

多边形面元 Mesh

分的越精细拟合的越好。

量化误差可控（分的越精细拟合的越好）
应用于任意拓扑结构
支持动态调整
可以利用GPU高效运算

常见多边形面元

多边形面元（多边形剖分）

多边形

数学表征

性质

每条边至少属于一个多边形。

每个Q_i定义了多边形网格的一个面。

顶点的度=关联边的数目

多边形面元的边界

三角面元（三角剖分）

多边形面元，其中每个面是三角形。
简化数据结构
简化渲染
简化算法
每个面都是平面和凸的
任何多边形都可以三角化

数学表征

顶点V，边E，面F，

优点

简化数据结构
简化渲染
简化算法
每个面都是平面和凸的
任何多边形都可以三角化

如何将点云转换为面元？

delaunay 三角剖分准则

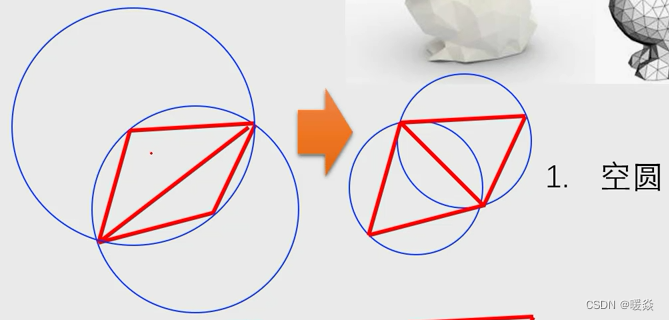
bowyer-watson 算法

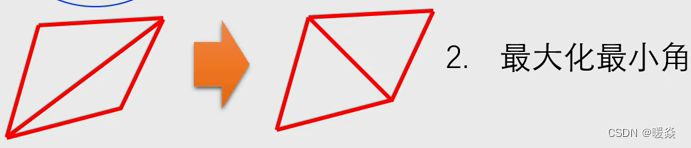
个人理解：最大化最小角应该是跟空圆本质要求是一样的，如果最小角不是最大就可能不是空圆。

体素

无序点云有序化（类比像素）
空间体素化，占用格点0, 1（格子越小精度越高）

优点

快速检测空间点是否被占据。
运算速度快。
体像素之间的逻辑运算。

体素是直接描述三维信息，所以在自动驾驶物体感知中也会经常使用到体素。

缺点

（稀疏）存储效率很低，特别在深度学习模型中问题突出。解决方法：稀疏卷积。

4 深度学习中的三维表征

4.1 点云研究中的三维表征

4.2 自动驾驶研究中的三维表征

5 点云的基本特征和描述

RGBD 两个不同视角下相比较，有相同有不同。

点云基本特征

按照特征的物理属性，可以将特征分为：几何域，强度域
按照特征的空间尺度，可以分为：单点特征，局部特征，全局特征

点云基本特征描述

法向量

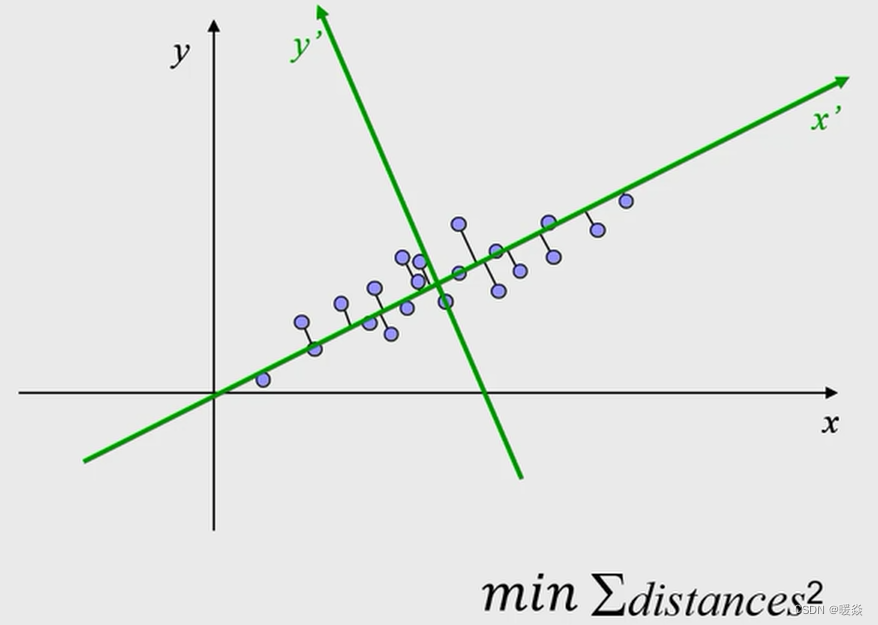
邻域

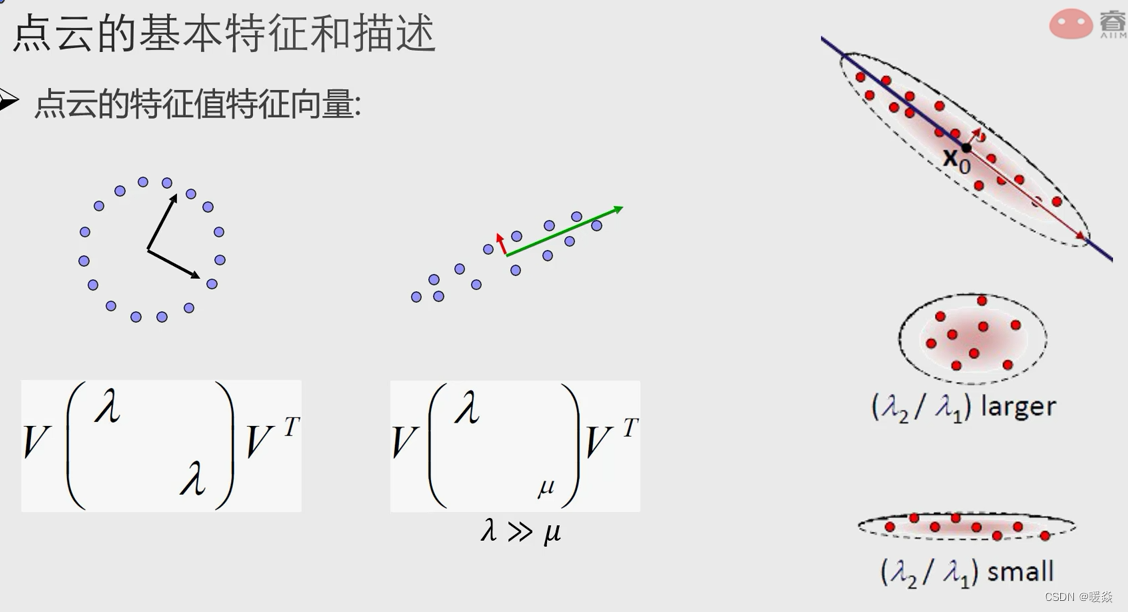
如何表述点云邻域？ - 协方差矩阵的特征基

一维拟合直线，二维拟合平面，三维拟合包围框。

数据集在某个基上的投影值(也是在这个基上的坐标值)越分散方差越大，这个基保留的信息也就越多。

信息量保存能力最大的基向量一定是的协方差矩阵的特征向量，并且这个特征向量保存的信息量就是它对应的特征值.

为什么协方差矩阵的特征向量是投影方差最大的方向？

证明一：拉格朗日乘数法

证明二：瑞利熵

不同特征值大小的描述