噪声系数与插入损耗

  在计算射频链路的级联噪声时，我们会输入每一级的噪声系数以及增益，即可计算出整个射频链路的噪声系数，用于系统评估。但是有同学问我，无源器件的噪声系数就是它的插入损耗吗？为什么呢？

噪声系数定义

  噪声系数是由信噪比定义的，即输入信噪比除以输出信噪比：
$$F=\frac{S_i/N_i}{S_o/N_o}$$

Friis噪声级联公式

  作为一个RF工程师，很多时候会需要评估整个系统的噪声系数，而如何通过各个器件的噪声系数而计算出整体的NF值呢？就是使用Friis噪声公式[1]：
$$F=F_1+\frac{F_2-1}{G_{p1}}+\frac{F_3-1}{G_{p1}{G}_{p2}}+...$$

  F为噪声系数，G代表各级增益，只要有各级器件自己的噪声系数和增益，通过上面的公式计算就可以计算出整个射频前端的总噪声系数，需要注意的是公式中的F和G都不是dB单位的，计算出整体的F后，再换算成dB即可，那么问题来了10log还是20log嘞？答：10log。那么问题又来了S参数是10log还是20log？留个小尾巴吧:)

  现代的仿真软件都可以帮助我们仿真计算这些参数，比如ADS, AWR, Cadence virtuoso等等都可以，当然这些软件也都价格不菲，对于爱好者和发烧友来说，可以使用网页版的计算器，也可以使用Avago公司做的AppCAD这样的免费的小软件来计算，如图1所示：

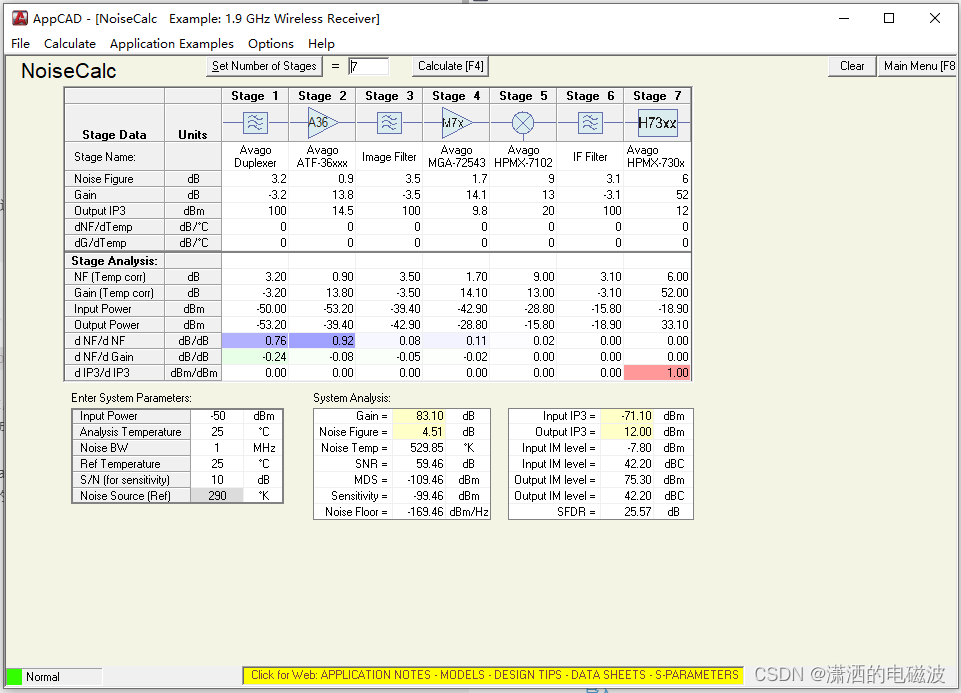
图1：AppCAD 计算噪声系数的界面 [2]

无源器件的噪声系数=插入损耗？

  无源器件的噪声系数就是其插入损耗，比如一颗SAW滤波器的插入损耗是-1.5dB，那么它的NF就是1.5dB。但是这是为什么呢？这是之前看到的一篇讲这个问题比较透彻的一篇文章：https://www.microwaves101.com/encyclopedias/noise-figure-of-passives，下面把这篇文章中的一些关键点提炼出来，并改写简化了证明思路，方便理解。
首先，能量进入任何器件都会有这样几个结果：（1）被器件耗散；（2）被反射；（3）继续向前传输。由此可以写出下面的方程：
$$P_{dissipated}=P_{incident}-P_{reflected}-P_{transmitted}$$
  如果我们将各个部分对输入的能量$P_{incident}$做归一化，则有：
$$P_{dissipated}/P_{incident}=1-P_{reflected}/P_{incident}-P_{transmitted}/P_{incident}$$
  根据S参数的定义可知$P_{reflected}/P_{incident}$即为反射系数$S_{11}$，$P_{transmitted}/P_{incident}$ 即为 $S_{21}$，因此，可以进一步写为：
$$P_{dissipated}/P_{incident}=1-|S_{11}{|}^2-|S_{21}{|}^2$$
  即：
$$P_{dissipated}=(1-|S_{11}{|}^2-|S_{21}{|}^2)\times P_{incident}$$
  下一步精彩的来了，器件的噪声的产生其实刚好是上面电能耗散变成发热的逆过程，即发热的能量变成“电信号”的过程，而这样产生的“电信号”其实就是噪声$P_{noise}$，因此对比上式可得：
$$P_{noise}(W/Hz)=(1-|S_{11}{|}^2-|S_{21}{|}^2)\times kT$$

  按照本文最开始介绍的噪声系数的公式，可得：
$$F=\frac{S_i/N_i}{S_o/N_o}=\frac{S_i/N_i}{G{S}_i/(G{N}_i+N_a)}=1+\frac{N_a}{G{N}_i}$$
  $N_a$是器件自己产生的噪声，可用上面介绍的$P_{noise}$代表；在$T_0$温度下，$N_i$输入的噪声可以用$k{T}_0$，即我们常说的$-174dBm/Hz$；$G$就是增益，即$|S_{21}{|}^2$，全部带入上式则有：
$$F=1+\frac{N_a}{G{N}_i}=1+\frac{(1-|S_{11}{|}^2-|S_{21}{|}^2)\times kT}{|S_{21}{|}^{2}k{T}_0}$$
  因此在$T_0$（$290K$）温度下，上式中$T=T_0$，进一步简化：
$$F=1+\frac{N_a}{G{N}_i}=1+\frac{(1-|S_{11}{|}^2-|S_{21}{|}^2)\times k{T}_0}{|S_{21}{|}^{2}k{T}_0}=1+\frac{1}{|S_{21}{|}^2}-\frac{|S_{11}{|}^2}{|S_{21}{|}^2}-1$$
  在50欧姆匹配的情况下，$S_{11}=0$，因此：
$$F=\frac{1}{|S_{21}{|}^2}$$
  $|S_{21}{|}^2$是器件的增益，其倒数就是插入损耗。以上就是简化版的无源器件的噪声系数=插入损耗的数学依据。其实从推导中我们也可以看出，这一说法并不严谨，因为实际上噪声系数和温度是密切相关的，在290K以上的温度，噪声系数大于插入损耗；在290K以下的温度，噪声系数小于插入损耗。

注：为了方便理解，本节推到做了简化，不如原文严谨，如需精准的数学推到请看原文。

S参数文件能用来仿真噪声系数吗

  在实际电路设计中如何仿真噪声系数呢，比如我想使用三极管来设计一个LNA，需要仿真其噪声系数，怎么做呢？最好的办法就是从厂家那里拿到该三极管的model，然后在仿真软件里加入该model，就可以仿真各种参数了。但是如果没有找到model，怎么办呢？用它的S参数文件能否仿真噪声系数吗？

  为了回答这个问题，我们回顾下S参数文件的构成：

! 满洲里国峰电子科技，www.guofengdianzi.com
! vitual RF BJT
! VCE =  1.5 V,  IC =  1.5 mA
! S-Parameters:                           
!  f/GHz     S11            S21            S12            S22
!         MAG   ANG      MAG   ANG      MAG   ANG      MAG   ANG
# GHz  S  MA  R  50
 0.100    0.1   -1.5       3   180     0.01   75        1    -5
1
2
3
4
5
6
7
8

  上面是我们虚构了一个射频晶体管的S参数文件，具体的S参数文件格式的介绍，可参看之前的博客《s2p标准格式》https://blog.csdn.net/mzldxf/article/details/107623579，然而这样的文件是不能够用来仿真噪声系数的，它可以仿真S参数，比如S11，S21等等。要想仿真S参数，它还需要NFmin这样的参数。一个既可以仿真S参数又可以仿真NF的sp文件是这样的：

! 满洲里国峰电子科技，www.guofengdianzi.com
! vitual RF BJT
! VCE =  1.5 V,  IC =  1.5 mA
! S-Parameters:                           
!  f/GHz     S11            S21            S12            S22
!         MAG   ANG      MAG   ANG      MAG   ANG      MAG   ANG
# GHz  S  MA  R  50
 0.100    0.1   -1.5       3   180     0.01   75        1    -5
 ...
!  f       NFmin   Gammaopt  Rn/50
! GHz       dB    MAG  ANG    -
 0.100      0.3   0.9   30   0.39
 ...
1
2
3
4
5
6
7
8
9
10
11
12
13

  与前者不同的地方在于多了这几行（省略号代表省略的其他频率的信息）。

!  f       NFmin   Gammaopt  Rn/50
! GHz       dB    MAG  ANG    -
 0.100      0.3   0.9   30   0.39
 ...
1
2
3
4

  $N{F}_{min}$就是该晶体管能够达到的最低的噪声，${\Gamma }_{opt}$是为了达到这样的噪声，最佳的$\Gamma$的位置，$R_n$描述匹配远离${\Gamma }_{opt}$点导致噪声增加的特性，$R_n$越大，斜率越陡，越不利于LNA的设计，通常$R_n/50$在0.4附近，最终的噪声系数和这些参数的关系如下 [4]：
$$F=F_{min}+\frac{4R_n}{Z_0}(\frac{|{\Gamma }_{opt}-{\Gamma }_s{|}^2}{|1+{\Gamma }_{opt}{|}^2(1-|{\Gamma }_s{|}^2)})$$

  其实在smith chart中，这样的公式就是一圈圈的噪声圆，比如我们再拿另外一组带有NFmin信息的S参数画在史密斯圆图上，就如下图所示：

图2：smith chart上的噪声圆[4]   图2中的Fmin=1.1dB，然后一圈一圈的增大（图2不与上面sp文件对应）。

  至此，我们介绍了无源器件的噪声系数和插入损耗的关系，捎带着讲述了一下噪声圆的仿真，希望对朋友们有所帮助~

作者：潇洒的电磁波（兴趣：射频芯片设计、雷达系统、嵌入式。欢迎大家合作交流。）
微信：GuoFengDianZi

引用：
[1] F. Ellinger. Radio Frequency Integrated Circuits and Technologies
[2] Avago Technologies. AppCAD.
[3] https://www.microwaves101.com/encyclopedias/noise-figure-of-passives
[4] Agilent. Fundamentals of RF and Microwave Noise Figure Measurements