-
对MMVAE中IWAE代码实现的理解
原始的IWAE
优化目标:
L I W A E ( x 1 : M ) = E z 1 : K ∼ q Φ ( z ∣ x 1 : M ) [ log ∑ k = 1 K 1 K p Θ ( z k , x 1 : M ) q Φ ( z k ∣ x 1 : M ) ] ( 1 ) \mathcal{L}_{\mathrm{IWAE}}\left(\boldsymbol{x}_{1: M}\right)=\mathbb{E}_{\boldsymbol{z}^{1: K} \sim q_{\Phi}\left(\boldsymbol{z} \mid \boldsymbol{x}_{1: M}\right)}\left[\log \sum_{k=1}^K \frac{1}{K} \frac{p_{\Theta}\left(\boldsymbol{z}^k, \boldsymbol{x}_{1: M}\right)}{q_{\Phi}\left(\boldsymbol{z}^k \mid \boldsymbol{x}_{1: M}\right)}\right] \quad\quad\quad(1) LIWAE(x1:M)=Ez1:K∼qΦ(z∣x1:M)[logk=1∑KK1qΦ(zk∣x1:M)pΘ(zk,x1:M)](1)这里 p Θ ( z , x 1 : M ) = p ( z ) ∏ m = 1 M p θ m ( x m ∣ z ) p_{\Theta}\left(\boldsymbol{z}, \boldsymbol{x}_{1: M}\right)=p(\boldsymbol{z}) \prod_{m=1}^M p_{\theta_m}\left(\boldsymbol{x}_m \mid \boldsymbol{z}\right) pΘ(z,x1:M)=p(z)∏m=1Mpθm(xm∣z)
后验分布由推理网络近似得到 q Φ ( z k ∣ x 1 : M ) q_{\Phi}\left(\boldsymbol{z}^k \mid \boldsymbol{x}_{1: M}\right) qΦ(zk∣x1:M)MMVAE中的IWAE变体
采用MoE方法进行多模态融合的优化目标:
L I W A E M o E ( x 1 : M ) = 1 M ∑ m = 1 M E z m 1 : K ∼ q ϕ m ( z ∣ x m ) [ log 1 K ∑ k = 1 K p Θ ( z m k , x 1 : M ) q Φ ( z m k ∣ x 1 : M ) ] ( 2 ) \mathcal{L}_{\mathrm{IWAE}}^{\mathrm{MoE}}\left(\boldsymbol{x}_{1: M}\right)=\frac{1}{M} \sum_{m=1}^M \mathbb{E}_{\boldsymbol{z}_m^{1: K} \sim q_{\phi_m}\left(\boldsymbol{z} \mid \boldsymbol{x}_m\right)}\left[\log \frac{1}{K} \sum_{k=1}^K \frac{p_{\Theta}\left(\boldsymbol{z}_m^k, \boldsymbol{x}_{1: M}\right)}{q_{\Phi}\left(\boldsymbol{z}_m^k \mid \boldsymbol{x}_{1: M}\right)}\right] \quad\quad\quad(2) LIWAEMoE(x1:M)=M1m=1∑MEzm1:K∼qϕm(z∣xm)[logK1k=1∑KqΦ(zmk∣x1:M)pΘ(zmk,x1:M)](2)根据MoE方法近似的后验分布为: q Φ ( z ∣ x 1 : M ) = ∑ m α m ⋅ q ϕ m ( z ∣ x m ) q_{\Phi}\left(\boldsymbol{z} \mid \boldsymbol{x}_{1: M}\right)=\sum_m \alpha_m \cdot q_{\phi_m}\left(\boldsymbol{z} \mid \boldsymbol{x}_m\right) qΦ(z∣x1:M)=∑mαm⋅qϕm(z∣xm),这里 α = 1 M \alpha = \frac{1}{M} α=M1
计算IWAE的主体代码:

- .log_prob(value)是计算value在定义的概率分布中对应的概率的对数。
- log_mean_exp(value)在后面介绍
在for循环里面一行行的分析,以r=0为例:
- lpz = l o g p ( z 1 ) log p(z_1) logp(z1), 每个潜在变量的尺寸:[K, batch size, latent dim],在这里用sum(-1)相当于是将潜在变量由latent dim压缩到1维
- lqz_x = l o g [ q ( z 1 ∣ x 1 ) + q ( z 1 ∣ x 2 ) ] log [ q(z_1 | x_1) + q(z_1 | x_2)] log[q(z1∣x1)+q(z1∣x2)]
- lpx_z = l o g p ( x 1 ∣ z 1 ) + l o g p ( x 2 ∣ z 1 ) logp(x_1|z_1) + logp(x_2|z_1) logp(x1∣z1)+logp(x2∣z1)
- lw = lpz + lpx_z + lqz_x
最后运算:
l1 = log_mean_exp(lw, dim=0)- 1
就可以得到: p ( z 1 ) ⋅ ( x 1 ∣ z 1 ) ⋅ ( x 2 ∣ z 1 ) q ( z 1 ∣ x 1 ) + q ( z 1 ∣ x 2 ) ( 3 ) \cfrac{p(z_1)\cdotp(x_1|z_1)\cdotp(x_2|z_1)}{q(z_1|x_1) + q(z_1|x_2)} \quad\quad\quad(3) q(z1∣x1)+q(z1∣x2)p(z1)⋅(x1∣z1)⋅(x2∣z1)(3)
这个结果就是上述公式2中m=1时的结果,这样一行行的分析就可以很好的理解上述代码是如何实现IWAE多模态变体的。
log_mean_exp
其中log_mean_exp的代码:
def log_mean_exp(value, dim=0, keepdim=False): return torch.logsumexp(value, dim, keepdim=keepdim) - math.log(value.size(dim))- 1
- 2
log_mean_exp和torch.logsumexp的区别就是字面意思,前面取平均,后者求和
- 因为MMVAE中的后验分布为
q
Φ
(
z
∣
x
1
:
M
)
=
∑
m
α
m
⋅
q
ϕ
m
(
z
∣
x
m
)
q_{\Phi}\left(\boldsymbol{z} \mid \boldsymbol{x}_{1: M}\right)=\sum_m \alpha_m \cdot q_{\phi_m}\left(\boldsymbol{z} \mid \boldsymbol{x}_m\right)
qΦ(z∣x1:M)=∑mαm⋅qϕm(z∣xm),这里
α
=
1
M
\alpha = \frac{1}{M}
α=M1,即需要对上述式子3中的分母取平均,所以log_mean_exp可以写成下述公式:
logmeanexp ( x ) i = log 1 j ∑ j exp ( x i j ) = log ∑ j exp ( x i j ) − log j \operatorname{logmeanexp}(x)_i=\log \frac{1}{j}\sum_j \exp \left(x_{i j}\right) = \log \sum_j \exp (x_{i j}) - \log j logmeanexp(x)i=logj1j∑exp(xij)=logj∑exp(xij)−logj - torch.logsumexp的介绍截图自官网:
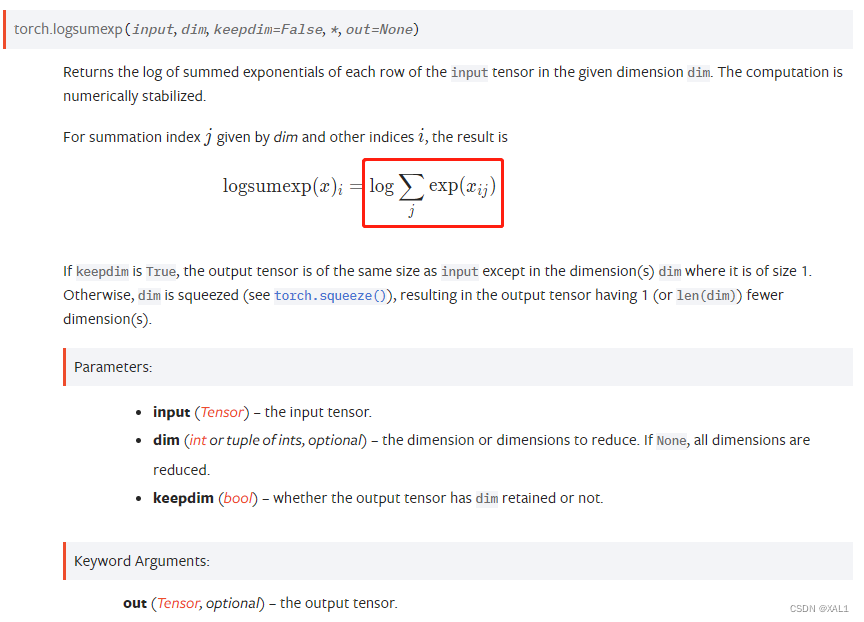
-
相关阅读:
【牛客刷题-SQL】SQL3 查询结果去重
算法---矩阵中战斗力最弱的 K 行(Kotlin)
IDERA ER/Studio Data Architect Professional v19.3.2
iOS开发之编译OpenSSL静态库
Sentinel使用教程
做前端,看完这篇文章你也可以做到
C++容器适配器操作总结(代码+示例)
个性化推荐的工业级实现
makefile-c
人工智能算法工程师(中级)课程8-PyTorch神经网络之神经网络基础与代码详解
- 原文地址:https://blog.csdn.net/weixin_45607635/article/details/127888665