2022.11.15-二分图专练

目录

50 years, 50 colors(HDU-1498)

Uncle Tom's Inherited Land*(HDU-1507)

Matrix(HDU-2119)

Arbiter(HDU-3118)

[ZJOI2007]矩阵游戏(黑暗爆炸1059)

Jimmy’s Assignment(HDU-1845)

---

50 years, 50 colors(HDU-1498)

原题链接:传送门

题意:一个n*n的矩阵中，有不同颜色的气球，气球的颜色最多50种（从1到50）。游戏开始前，先选择一种颜色。游戏开始后，每次选择一行或者一列包含该种颜色的气球进行撞击。如果选择行，那么这一行的气球都会炸裂。如果选择列，这一列的气球都炸裂。求有多少种颜色的气球，无论怎么玩，都不能在K次之内，把所有同色的气球都撞裂。

思路:直接模拟题目过程，每次把当前要处理的颜色预处理出来，我们可以把横坐标看做左部，纵坐标看做右部，由此形成一个二分图 ，问题转化为：求每个颜色的二分图的最小点覆盖。最小点覆盖=最大匹配数。

#include 
using namespace std;
const int N = 125;
int n, k;
int g[N][N], gc[N][N], match[N];
bool vis[N];
 
int dfs(int x){
  for(int j = 1; j <= n; j++){
    if(gc[j][x] && !vis[j]){
      vis[j] = true;
      if(!match[j] || dfs(match[j])){
        match[j] = x;
        return 1;
      }
    }
  }
  return 0;
}
 
int main(){
  while(scanf("%d%d", &n, &k), n || k){
    for(int i = 1; i <= n; i++)
      for(int j = 1; j <= n; j++)
        scanf("%d", &g[i][j]);
    bool flag = 0;
    for(int c = 1; c <= 50; c++){
      for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
          gc[i][j] = (g[i][j] == c);
      memset(match, 0,sizeof match);
      int ans = 0;
      for(int i = 1; i <= n; i++){
        memset(vis, 0, sizeof vis);
        ans += dfs(i);
      }
      if(ans > k){
        if(flag) printf(" ");
        printf("%d", c), flag = 1;
      }
    }
    if(!flag) puts("-1");else puts("");
  }
  return 0;
}

Uncle Tom's Inherited Land*(HDU-1507)

原题链接:传送门

题意:给你一个n*m的地，然后给你p个点，表示这些点代表的地是不能卖的，问你最多能卖出多少块1*2的地。

思路:经典的放置问题，根据棋盘的特性

 我们能看出来如果放置任意一个条子，都是由两种颜色组成，由此我们可以把横纵坐标相加的奇偶性来当做两个点集的部分，由此求得的最大匹配就是最多放置的数。

#include 
using namespace std;
typedef pair<int, int> PII;
const int N = 125;
int n, m, k;
PII match[N][N];
bool vis[N][N], g[N][N];
 
const int dx[] = {1, -1, 0, 0};
const int dy[] = {0, 0, 1, -1};
 
int dfs(int x, int y){
  for(int i = 0; i < 4; i++){
    int a = x + dx[i], b = y + dy[i];
    if(a < 1 || a > n || b > m || b < 1) continue;
    if(g[a][b] || vis[a][b]) continue;
    vis[a][b] = true;
    auto t = match[a][b];
    if(t.first == -1 || dfs(t.first, t.second)){
      match[a][b] = {x, y};
      return 1;
    }
  }
  return 0;
}
 
int main(){
  while(~scanf("%d%d", &n, &m), n || m){
    scanf("%d", &k);
    memset(g, 0, sizeof g);
    while(k--){
      int u, v;
      scanf("%d%d", &u, &v);
      g[u][v] = 1;
    }
    int ans = 0;
    memset(match, -1, sizeof match);
    for(int i = 1; i <= n; i++)
      for(int j = 1; j <= m; j++)
        if((i + j) % 2 && !g[i][j]){
         memset(vis, 0, sizeof vis);
         ans += dfs(i, j);
        }
    printf("%d\n", ans);
    for(int i = 1; i <= n; i++)
      for(int j = 1; j <= n; j++){
        if(match[i][j].first != -1 && match[i][j].second != -1){
          printf("(%d,%d)--(%d,%d)\n",match[i][j].first, match[i][j].second, i, j);
        }
      }
  }
  return 0;
}

Matrix(HDU-2119)

原题链接:传送门

题意:一个只有01组成的矩阵，每次可以把一行或一列所有的1变成0，问最少多少次能把所有的1清除

思路:有点像气球那题的简易版，横坐标看做左部，纵坐标看做右部，由此形成一个二分图 ，问题转化为：求每个颜色的二分图的最小点覆盖。最小点覆盖=最大匹配数。

#include 
using namespace std;
const int N = 125;
int n, m, k;
int g[N][N], gc[N][N], match[N];
bool vis[N];
 
int dfs(int x){
  for(int j = 1; j <= n; j++){
    if(g[j][x] && !vis[j]){
      vis[j] = true;
      if(!match[j] || dfs(match[j])){
        match[j] = x;
        return 1;
      }
    }
  }
  return 0;
}
 
int main(){
  while(scanf("%d", &n), n){
    scanf("%d", &m);
    for(int i = 1; i <= n; i++)
      for(int j = 1; j <= m; j++)
        scanf("%d", &g[i][j]);
    bool flag = 0;
    memset(match, 0,sizeof match);
    int ans = 0;
    for(int i = 1; i <= m; i++){
      memset(vis, 0, sizeof vis);
      ans += dfs(i);
    }
    printf("%d\n", ans);
  }
  return 0;
}

Arbiter(HDU-3118)

很不错的一道题，特别值得一刷~

题意:每组给出 n 个点以及 m 条无向边，已知每次经过一条边，手性会发生改变，即从左撇子变为右撇子或从右撇子变成左撇子，现在某个人从自己的点出发，要求他无论如何走，当他回到自己的点时，手性不发生改变，问最少删除多少条边

题意简化:给定一张图，问,删除给出的图中的最少的边，让图无奇数边的环？

思路：状态压缩+二分图, 我们可以发现每个点最多都有两种状态(左/右),那么总共就有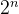种情况，那么我们可以由每个点的方向(左/右)分成两个点集，最后的问题就是删除最少的边使之变成一个二分图，二分图的一个充要条件就是同一部分不能有边，那么我们就把同一部分有边的删掉，所以只需要枚举二进制子集保证在同一部分不能有边即可。

#include 
using namespace std;
const int N = 125;
const int INF = 0x3f3f3f3f;
int n, m, k, t;
int g[N][N];
 
int main(){
  scanf("%d", &t);
  while(t--){
    scanf("%d%d", &n, &m);
    if(!n || !m){ puts("0"); continue;}
    memset(g, 0, sizeof g);
    while(m--){
      int u, v;
      scanf("%d%d", &u, &v);
      ++g[u][v], ++g[v][u];
    }
    int res = INF;
    for(int i = 1; i < (1 << n) ; i++){
      int cnt = 0;
      for(int j = 0; j < n; j++){
        for(int k = j + 1; k < n; k++){
          if((i & (1 << j)) == 0 && (i & (1 << k)) == 0) cnt += g[j][k];
          else if((i & (1 << j)) && (i & (1 << k))) cnt += g[j][k];
        }
      }
      res = min(res, cnt);
    }
    printf("%d\n", res);
  }
  return 0;
}

[ZJOI2007]矩阵游戏(黑暗爆炸1059)

原题链接:传送门

中文题面，题意不过多赘述。

思路：同样的横坐标纵坐标分为两部分以此构成一个二分图。我们只需要对行进行匹配即可。

#include 
using namespace std;
const int N = 5000;
const int INF = 0x3f3f3f3f;
int n, m, k, t, x;
int h[N], e[N * N], ne[N * N], idx; 
int g[N][N], match[N];
bool vis[N];
 
void add(int a, int b){
  e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
 
int dfs(int x){
  for(int i = h[x]; i != -1; i = ne[i]){
    int j = e[i];
    if(vis[j]) continue;
    vis[j] = true;
    if(match[j] == -1 || dfs(match[j])){
      match[j] = x;
      return 1;
    }
  }
  return 0;
}
 
int main(){
  scanf("%d",  &t);
  while(t--){
    memset(h, -1, sizeof h);
    memset(match, -1, sizeof match);
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
      for(int j = 1; j <= n; j++){
        scanf("%d", &x);
        if(x) add(i, j);
      }
      int ans = 0;
      for(int i = 1; i <= n; i++){
        memset(vis, 0, sizeof vis);
        if(dfs(i)) ans++;
		else break;
      }
      puts(ans == n ? "Yes" : "No");
  }
  return 0;
}

Jimmy’s Assignment(HDU-1845)

原题链接:传送门

题意：给一n个点的三正则图，求最大匹配。

思路：建双向边，找最大匹配数

#include 
using namespace std;
const int N = 5500;
const int INF = 0x3f3f3f3f;
int n, m, k, t, x;
int h[N], e[N * N], ne[N * N], idx; 
int g[N][N], match[N];
bool vis[N];
 
void add(int a, int b){
  e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
 
int dfs(int x){
  for(int i = h[x]; i != -1; i = ne[i]){
    int j = e[i];
    if(vis[j]) continue;
    vis[j] = true;
    if(match[j] == -1 || dfs(match[j])){
      match[j] = x;
      return 1;
    }
  }
  return 0;
}
 
int main(){
  scanf("%d",  &t);
  while(t--){
    memset(h, -1, sizeof h);
    memset(match, -1, sizeof match);
    scanf("%d", &n);
    int m = 3 * n / 2, ans = 0;
    while(m--){
      int a, b;
      scanf("%d%d", &a, &b);
      add(a, b), add(b, a);
    }
    for(int i = 1; i <= n; i++){
      memset(vis, 0, sizeof vis);
      ans += dfs(i);
    }
    printf("%d\n", ans >> 1);
  }
  return 0;
}

 大神思路新浪博客，根据握手定理得n一定是偶数，由于三正则图，而且题目提示是2边连通，所以图中不存在桥，也就是一定可以找到一条回路经过每个顶点至少一次（强连通的定义：强连通图一定存在一条回路记过每个顶点至少一次）由于是三则图，每个顶点的度是3，如果这条回路经过某个顶点2次，那么这个顶点的度就是4，这个和条件矛盾。
这条经过每个顶点一次的交错路就可以作出n/2匹配。

#include
 
using namespace std;
 
int main() {
    int t, n, a, b, i;
    cin >> t;
    while (t--) {
        cin >> n;
        for (i = 0; i < n * 3 / 2; i++)cin >> a >> b;
        cout << n / 2 << endl;
    }
    return 0;
}