-
三步学会如何构建平衡二叉树(简单好理解)
何为平衡二叉树?
首先回顾一下,什么是平衡二叉树(亦被称为AVL树,Adelson-Velskii and Landis)。平衡二叉树主要具有以下三个特点:
1. 平衡二叉树首先要符合搜索二叉树的特点:即左子树的值比根节点小,右子树的值比根节点大;
2. 左子树和右子树的高度之差的绝对值小于等于1
3. 左子树和右子树也是平衡二叉树判断方法:左子树和右子树的高度差称为平衡因子(平衡因子=左子树高度-右子树高度),若平衡因子绝对值>1,则该二叉树不平衡。
当二叉树的子树间的高度相差太大时,其操作的时间复杂度会提高到O(n)。为了降低时间复杂度,需要对二叉树进行处理,形成平衡二叉树。
构建平衡二叉树
平衡二叉树的构建,可以通过以下三步来完成:
1. 判断二叉树类型(LL, LR, RR, RL)
LL型 LR型 RL型 RR型 先理解上面四种类型,如何变为平衡二叉树:
首先:二叉树的平衡需要通过“左旋”“右旋”来处理。可以把二叉树想象成一个搭在三角坡上的链条,其支撑点就是根节点(三个节点的中间值),左旋右旋都是在这个三角坡上进行处理。1)LL型(左型)需要“右旋”。看图理解:
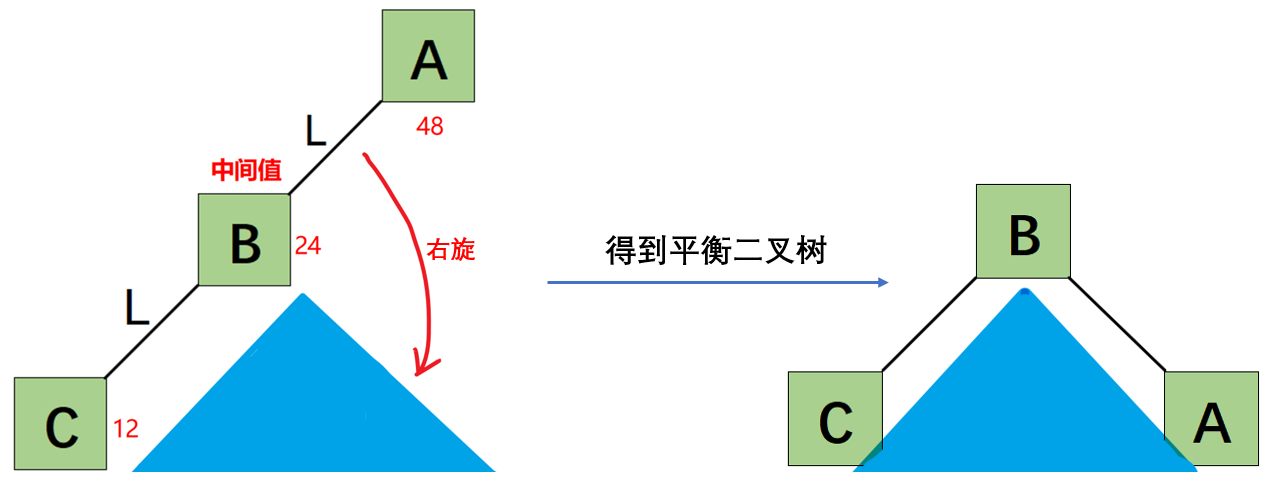
LL型右旋变为平衡二叉树 2)LR型(左型)需要“右旋”。看图理解:

LR型右旋变为平衡二叉树 3)RR型、RL型与上述两方法一致,不再赘述。
2. 找出不平衡的地方
如果一个二叉树里混合了LR和RL等多种类型,可以优先从由根节点构成的不平衡二叉树开始处理。举两个例子说明:

上面的不平衡二叉树中,红色部分是RL型,蓝色部分是LR型,但24、53、37是根节点,由它们构成的RL树更重要。而53、37、48构成的LR树中,48不是根节点,所以不处理(因为先处理了最重要的不平衡结构,后面的不平衡处都会随之解体)。该不平衡二叉树具体的平衡过程会在后文详细给出。

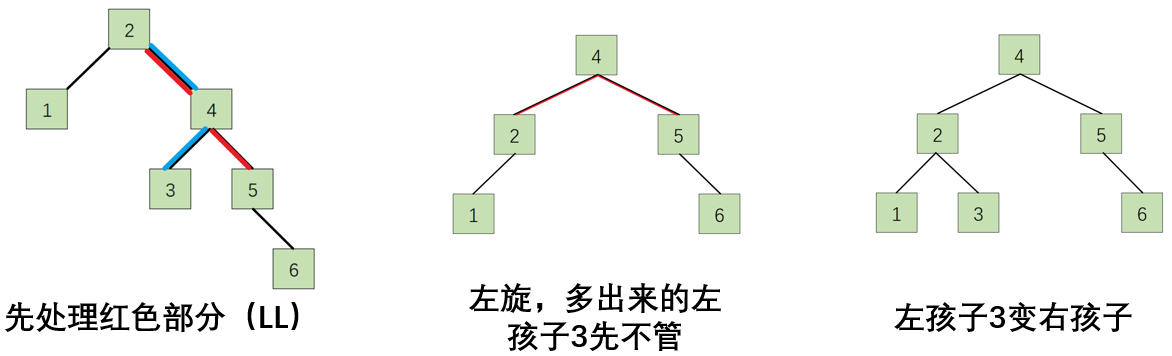
上述二叉树中,红色部分是RR型,蓝色部分是RL型,其中2、4、5是根节点,由它们构成的RR树更重要,优先处理。而蓝色部分由2、4、3构成,3不是根节点,不处理。
3. 旋转,直到得到平衡二叉树
原则:
1. 先处理由根节点组成的不平衡树,后面的不平衡都会迎刃而解。
2. 多余的右孩子要变成左孩子
例1:
例2:
例3:
输入关键字序列(16,3,7,11 ,9,26,18,14,15)给出AVL树
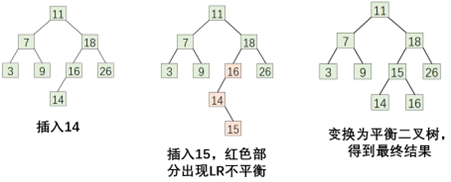
-
相关阅读:
CASIO fx4850万能坐标计算程序
前端三刺客---CSS
R语言读取(加载)txt格式数据为dataframe、查询dataframe中存在缺失值的行
C#语言实例源码系列-实现滚动字幕
以太网ARP测试实验
公务员备考(二十) 申论
通达信软件L2接口的委托队列有什么用?
Linux Server 终止后立即重启报错 bind error: Address already in use
Java for循环倒序输出
buu(sql注入)
- 原文地址:https://blog.csdn.net/Leeeoplod/article/details/127859225