概率 | 【提神醒脑】重难点专题突破 自用笔记

        本文总结参考于 kira 2023概率提神醒脑技巧班 中 —— 重难点专题。

        笔记均为自用整理。加油！ヾ(◍°∇°◍)ﾉﾞ

        一研为定！

---

一、条件均匀 / 指数 / 二项…分布

---------------------------------------------------------------------------------------------------------------------------------

【例2.19】 全概率公式 

         

 【解析】

        欲求 概率密度 ，先写分布函数。

                 

【注】

         

        

         

        

        

                 

--------------------------------------------------------------------------------------------------------------------------------

【例2.20】

        

                

---

二、求一维随机变量函数Y = g (X)分布

（分布函数等号跟大于号，概率密度不要等号） 

---

---------------------------------------------------------------------------------------------------------------------------------

【例2.14】分布律：抓两点 ① 取值  ② 概率

        

【解析】

         

---------------------------------------------------------------------------------------------------------------------------------

        ① 分布函数法（画出X和Y的关系图 多一笔也不要画，注意X的定义域 ，求出曲线在直线下方的X的取值范围，分段积分）

        ② 公式法（y是x的严格单调可导函数）

        

        

        

-------------------------------------------------------------------------------------------------------------------------------- 

【例2.15】连续型 Y = g(X)

         

         

          --------------------------------------------------------------------------------------------------------------------------------

 ❤※☆ —— 当X为连续型随机变量，Y=F(X)服从 U(0,1)

【例2.16】当X为连续型随机变量，Y=F(X)服从 U(0,1)

        

【解析】 背结论！

         

        

--------------------------------------------------------------------------------------------------------------------------------

【例2.17】

        

注：这里的F(x)不是分布函数。

         

 --------------------------------------------------------------------------------------------------------------------------------

【例2.18】依旧是 Y=g(X)

        

         

---

三、求二维随机变量函数Z = g(X, Y)分布

先判断 X和Y的 类型！

但Z依旧是一维随机变量！一元函数。

--------------------------------------------------------------------------------------------------------------------------------

【例3.11】依旧是 Y=g(X)

        

【解析】分布律：① 取值  ② 概率

        

---

        

        

        可卷积：能反解出单值反函数 + 只用概率密度    

        

 --------------------------------------------------------------------------------------------------------------------------------

 【例3.12】

          

【解析】

         

         

        

         

注：卷积公式法的关键是 —— 解不等式组找准换元后的区域（有必要时结合图像) 

         

---

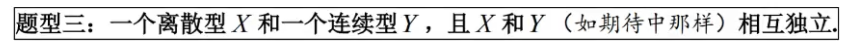
 -------------------------------------------------------------------------------------------------------------------------------- 【例3.13】分布函数法 + 对离散型全集分解

        

         

        

         

---

 -------------------------------------------------------------------------------------------------------------------------------- 【史诗级 2016 典型例题】

         

         

         

---

---

【2020 典型例题】

        

【解析】

最小值！这里好好想想哦 ~

         

         

---

---

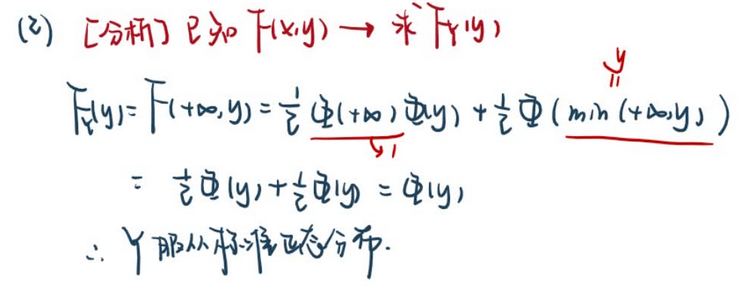
【例3.16】① 拿 U~N(μ,σ2)   ②默写 fU(u)

        

【解析】