左神算法（一）上修改版

​

序言：

左神（左程云）所讲课程有两套，一套为马士兵，一套为牛客。两套体系不好区分。
有基础班和训练营。基础班是基础，训练营前两节属于提升班（进阶版），提升班还是基础，不过难度比基础班高一些，建议掌握基础班和提升版的基础上学习训练营。
以下为 硬核！一周刷爆LeetCode，算法大神（左程云）耗时112天打造出算法与数据结构基础到高级全家桶教程+大厂面试真题详解_哔哩哔哩_bilibili
的 P2到P17

左神算法（一）上修改版

左神算法（一）下修改版

左神算法（二）

一、认识复杂度、对数器、二分法与异或运算

1.评估算法优劣的核心指标是什么？

时间复杂度（流程决定）

额外空间复杂度（流程决定）

常数项时间（实现细节决定）

2.何为常数时间的操作？

​

（1）解释：

如果一个操作的执行时间不以具体样本量为转移,每次执行时间都是固定时间。称这样的操作为常数时间的操作。
​​

（2）常见的常数时间的操作：

• 常见的算术运算(+、-、*、/、%等)
• 常见的位运算(>>、>>>、<<、&、^等)
• 赋值、比较、自增、自减操作等
• 数组寻址操作

总之,执行时间固定的操作都是常数时间的操作。
反之,执行时间不固定的操作,都不是常数时间的操作。

拓展

位运算：
>>：带符号右移
>>>：不带符号右移

可见他人的博客：
Java中位运算的解析
java的位运算解析（&/|/~/^/>>/<>>）

解释：
原来的数字最高位就是符号位，带符号右移就是把原来的数字都右移1位后，最高位补一个原来数字的符号位。不带符号右移就是把原来的数字都右移1位后，最高位补一个0。

对于“带符号右移和不带符号右移”举例：
若一个整型数字32位：000000…11000
带符号右移就变为XX：000000…01100
不带符号右移XXXXX：000000…01100

举例：LinkedList就不是常数时间的操作：

​​​​

数组底层是一个连续区间，可以算出偏移量取出来。而LinkedList底层是指针移动找下一个节点，不是连续期间，此时list.get(i)就不是一个常数时间的操作，它需要遍历才行。

时间复杂度就是衡量这个流程中发生了多少次常数操作。

对于“时间复杂度就是衡量这个流程中发生了多少次常数操作”的举例：选择排序

一个无序数组arr，0到N-1位置找最小值与0位置交换
1到N-1位置找最小值与1位置交换
…
每行都要看+比，再来一次交换。



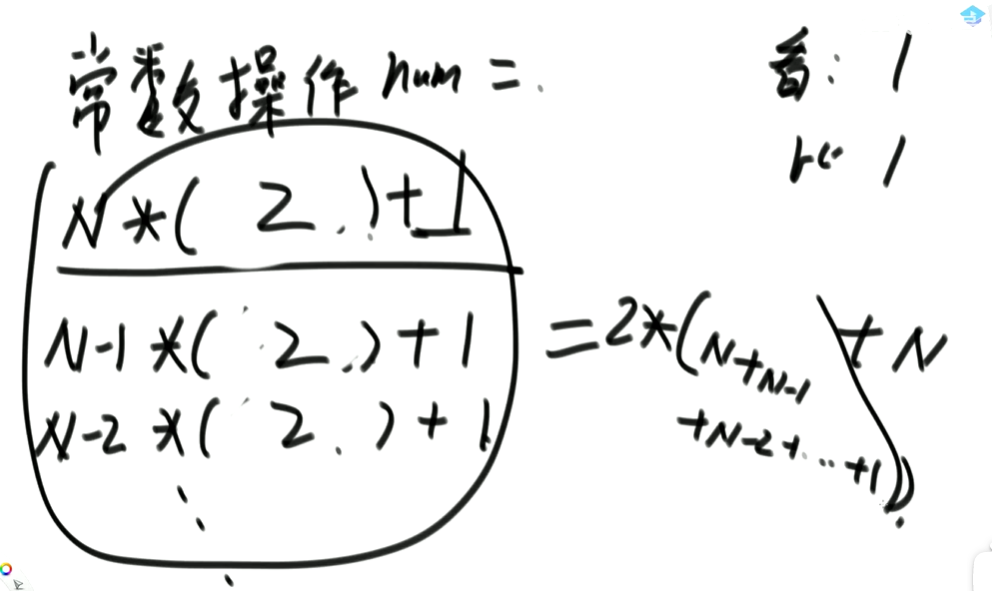
常数操作 num
num = N * (看+比)+交换 + (N-1) * (看+比)+交换+…
看=1，比=1，交换=1.其中有时交换会发生，有时交换不会发生，有时交换为0有时为1.时间复杂度是不计算常数项的，所以交换可以不精确。
所以 num = N * (1+1)+1 + (N-1) * (1+1)+1 + …
num = 2 * (N+N-1+…+1)+N

N+N-1+…+1为等差数列。
等差数列可以写为：

所以num=下图

又时间复杂度不考虑常数项、低次项和高次项系数。计算时间复杂度时不要太在意时间复杂度常数项的多少，粗略计算就可以，因为反正最后也不会考虑常数项。所以 选择排序的时间复杂度为N的平方。

选择排序的最好、最坏时间复杂度都是N的平方。

3.如何确定算法流程的总操作数量与样本数量之间的表达式关系？

1. 想象该算法流程所处理的数据状况,要按照最差情况来。
2. 把整个流程彻底拆分为一个个基本动作,保证每个动作都是常
   数时间的操作。
3. 如果数据量为N,看看基本动作的数量和N是什么关系。

对于第二点拆分到位的解释：
就如上方选择排序的举例，其中的看+比+换都是最基本的动作单位。

4.如何确定算法流程的时间复杂度？

当完成了表达式的建立,只要把最高阶项留下即可。低阶项都去掉,
高阶项的系数也去掉。
记为:O(忽略掉系数的高阶项)

当样本量足够大的时候，即N趋向于很大很大的时候，除了高次项其他都不重要了。

举例：
两个表达式，然而当N足够大的时候，很明显N的平方的表达式时间复杂度是小于N的三次方的表达式的时间复杂度。

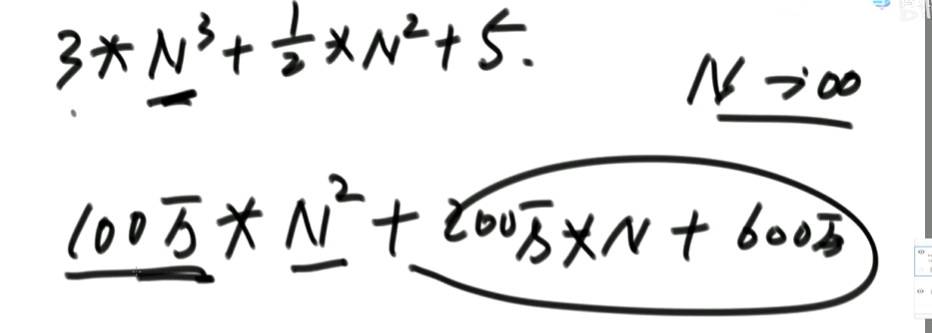
5.时间复杂度的意义

抹掉了好多东西,只剩下了一个最高阶项啊…
那这个东西有什么意义呢?
时间复杂度的意义在于：
当我们要处理的样本量很大很大时,我们会发现低阶项是什么不是最重要的;每一项的系数是什么不是最重要的。真正重要的就是最高阶项是什么。
这就是时间复杂度的意义,它是衡量算法流程的复杂程度的一种指标,该指标只与数据量有关.与过程之外的优化无关。

6.通过三个具体的例子，来实践一把时间复杂度的估算

选择排序、冒泡排序、插入排序的时间复杂度都是O(N ^ 2)。选择排序，冒泡排序的时间复杂度不会因样本数据的状态而影响时间复杂度，而插入排序的时间复杂度会受到样本数据状态的影响。

（1）选择排序

过程：
arr[0 ~ N-1]范围上,找到最小值所在的位置，然后把最小值交换到0位置。
arr[1 ~ N-1]范围上,找到最小值所在的位置，然后把最小值交换到1位置。
arr[2 ~ N-1]范围上,找到最小值所在的位置，然后把最小值交换到2位置。
…
arr[N-1 ~ N-1])范围上,找到最小值位置，然后把最小值交换到N-1位置。

估算：
很明显,如果arr长度为N，每一步常数操作的数量如等差数列一般。所以，
总的常数操作数量 = a * (n ^ 2) + bn + c（a、b、c都是常数）
所以选择排序的时间复杂度为O(N ^ 2)。

相关概念、解释上面已经解释，代码如下：

package class01;

import java.util.Arrays;

public class Code01_SelectionSort {
   

	// 选择排序主方法
	public static void selectionSort(int[] arr) {
   
		if (arr == null || arr.length < 2) {
   
			return;
		}
		// 0 ~ N-1  找到最小值，在哪，放到0位置上
		// 1 ~ n-1  找到最小值，在哪，放到1 位置上
		// 2 ~ n-1  找到最小值，在哪，放到2 位置上
		for (int i = 0; i < arr.length - 1; i++) {
   
			int minIndex = i;
			for (int j = i + 1; j < arr.length; j++) {
    // i ~ N-1 上找最小值的下标 
				minIndex = arr[j] < arr[minIndex] ? j : minIndex;
			}
			swap(arr, i, minIndex);
		}
	}

	// 选择排序的交换数字方法
	public static void swap(int[] arr, int i, int j) {
   
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

	// 其他方法都是对数器的方法
	// for test
	public static void comparator(int[] arr) {
   
		Arrays.sort(arr);
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
   
		// Math.random()   [0,1)  
		// Math.random() * N  [0,N)
		// (int)(Math.random() * N)  [0, N-1]
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
   
			// [-? , +?]
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
   
		if (arr == null) {
   
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
   
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
   
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
   
			return false;
		}
		if (arr1 == null && arr2 == null) {
   
			return true;
		}
		if (arr1.length != arr2.length) {
   
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
   
			if (arr1[i] != arr2[i]) {
   
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
   
		if (arr == null) {
   
			return;
		}
		for (int i = 0; i < arr.length; i++) {
   
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
   
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
   
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			selectionSort(arr1);
			comparator(arr2);
			if (!isEqual(arr1, arr2)) {
   
				succeed = false;
				printArray(arr1);
				printArray(arr2);
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		selectionSort(arr);
		printArray(arr);
	}

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143

（2）冒泡排序

过程:
在arr[0 ~ N-1]范围上，arr[0]和arr[1]谁大谁来到1位置；arr[1]和arr[2]谁大谁来到2位置…arr[N - 2]和arr[N - 1]谁大谁来到N-1位置。
在arr[0 ~ N-2]范围上，重复上面的过程，但最后一步是arr[N - 3]和arr[N - 2]谁大谁来到N-2位置。
在arr[0 ~ N-3]范围上，重复上面的过程，但最后一步是arr[N - 4]和arr[N - 3]谁大谁来到N-3位置。
…
最后在arr[0 ~ 1]范围上，重复上面的过程，但最后一步是arr[0]和arr[1]谁大谁来到1位置。

估算：
很明显,如果arr长度为N.每一步常数操作的数量,依然如等差数列一般，所以,总的常数操作数量=a(N ^ 2) + b * N + c（a、b、c都是常数）
所以冒泡排序的时间复杂度为O(N^2)。

具体案例：

第一轮0位置到5位置比较，选出最大值到5位置，见下面的步骤（第二行为下标，第一行为值。）：

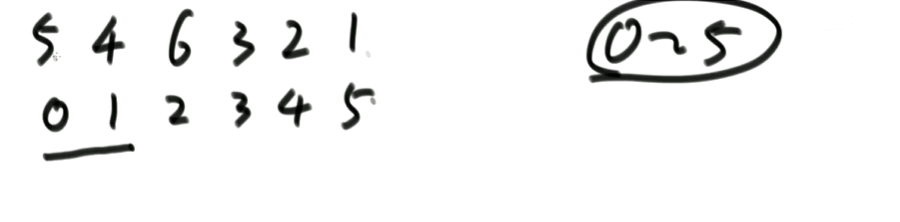
0位置与1位置比较大小，0位置大于1位置则交换两个值，由上图得下图。

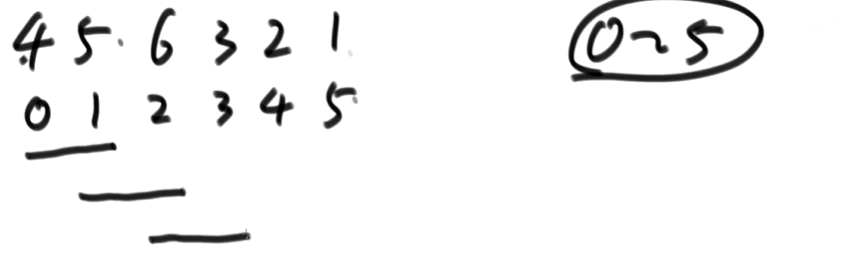
1位置和2位置比较，5<6所以不交换。
2位置和3位置比较，3<6所以交换，见下图。

3位置和4位置比较，由上图知，2<6，所以交换。4位置和5位置比较，由上图知，1<6，所以交换。两次交换结果如下。

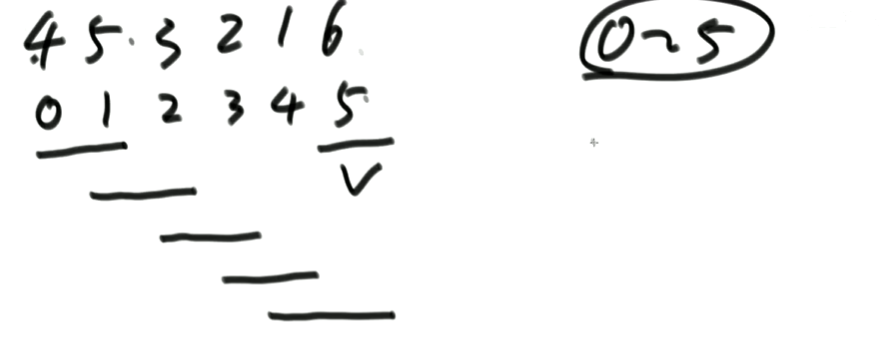
第一轮结束后最后成了上面这样，最大值选出来了。

第二轮0到4位置比较，选出第二大值到4位置。
…

假设有N个数字，冒泡排序是第一次进行N-1次比较，选取最大值放到N-1位置；第二次进行N-2次比较，选取第二大值放到N-2位置…所以冒泡排序的时间复杂度是O(N ^ 2)。

冒泡排序的代码如下：

package class01;

import java.util.Arrays;

public class Code02_BubbleSort {
   

	// 冒泡排序主方法
	public static void bubbleSort(int[] arr) {
   
		if (arr == null || arr.length < 2) {
   
			return;
		}
		// 0 ~ N-1
		// 0 ~ N-2
		// 0 ~ N-3
		for (int e = arr.length - 1; e > 0; e--) {
    // 0 ~ e
			for (int i = 0; i < e; i++) {
   
				// 两数相同则不交换。若为>=，则两数相同交换，两数相同交换多此一举。
				if (arr[i] > arr[i + 1]) {
   
					swap(arr, i, i + 1);
				}
			}
		}
	}

	// 交换arr的i和j位置上的值
	public static void swap(int[] arr, int i, int j) {
   
		arr[i] = arr[i] ^ arr[j];
		arr[j] = arr[i] ^ arr[j];
		arr[i] = arr[i] ^ arr[j];
	}

	// for test
	public static void comparator(int[] arr) {
   
		Arrays.sort(arr);
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
   
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
   
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
   
		if (arr == null) {
   
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
   
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
   
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
   
			return false;
		}
		if (arr1 == null && arr2 == null) {
   
			return true;
		}
		if (arr1.length != arr2.length) {
   
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
   
			if (arr1[i] != arr2[i]) {
   
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
   
		if (arr == null) {
   
			return;
		}
		for (int i = 0; i < arr.length; i++) {
   
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
   		
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
   
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			bubbleSort(arr1);
			comparator(arr2);
			if (!isEqual(arr1, arr2)) {
   
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		bubbleSort(arr);
		printArray(arr);
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137

（3）插入排序

过程:
想让arr[0 ~ 0]上有序，这个范围只有一个数，当然是有序的。
想让arr[0 ~ 1]上有序，所以从arr[1]开始往前看，如果arr[1] < arr[0]就交换。否则什么也不做。
想让arr[0 ~ i]上有序，所以从arr[i]开始往前看，arr[i]这个数不停向左移动，一直移动到左边的数字不再比自己大，停止移动。
最后一步,想让arr[0 ~ N-1]上有序，arr[N - 1]这个数不停向左移动，一直移动到左边的数字不再比自己大,停止移动。
估算时发现这个算法流程的复杂程度,会因为数据状况的不同而不同，你发现了吗?

具体案例：
0到0位置上有序，如下图：

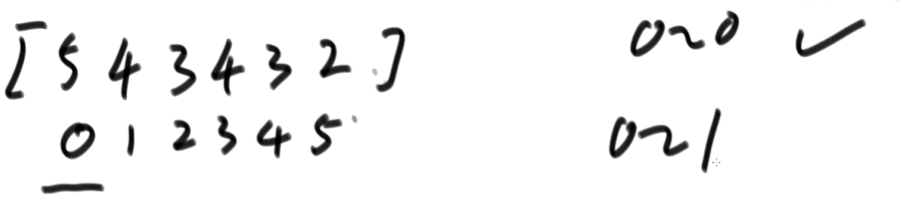
0到1位置上有序，如下图：

0到2位置上有序，2位置的3和1位置比较并交换，然后和0位置的4比较并交换，如下图：


…

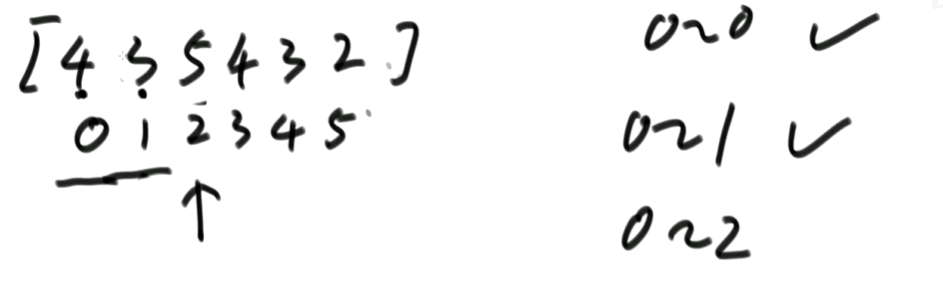
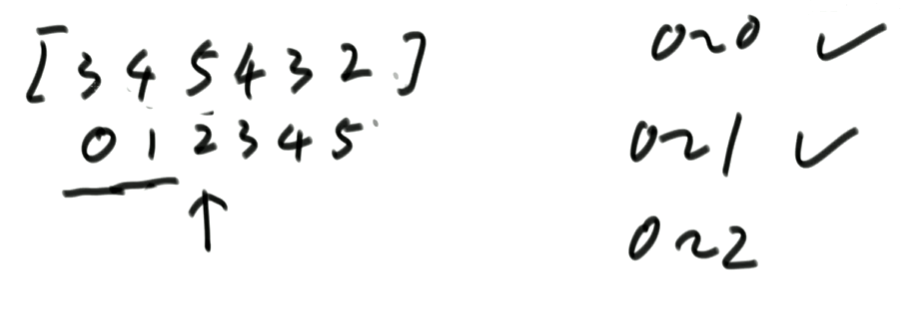
上面是倒数第二步…

插入一个笑话：这类似于打牌，新拿一张牌，按顺序排大小，一个学生并不理解这个例子，说：我打牌是把质数放在左边，非质数放在右边。

注意：这个算法的时间复杂度会受到样本数据的初始状况影响

举例—算法的时间复杂度会受到样本数据的初始状况影响：

好的情况：初始数据有序，见下图

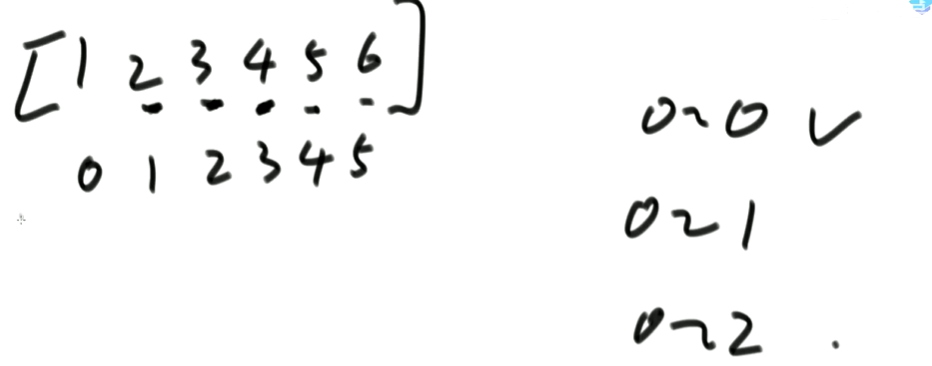
如上图，0到1位置比较，2比较1，有序；
0到2位置比较，3比较2，有序，此时3就不比较1了，且没有发生交换；
…
这就和上面的举例有了差距，此时时间复杂度是O(N)。

差的情况：见下图

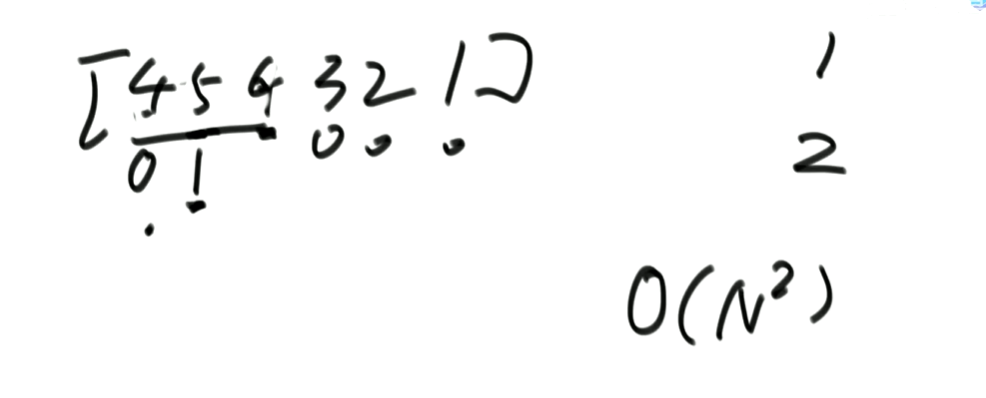
此时时间复杂度是O(N ^ 2）。

总结：然而我们考虑时间复杂度要拿最差情况作为时间复杂度的计算。

代码如下：

package class01;

import java.util.Arrays;

public class Code03_InsertionSort {
   

	public static void insertionSort(int[] arr) {
   
		if (arr == null || arr.length < 2) {
   
			return;
		}
		// 不只1个数
		for (int i = 1; i < arr.length; i++) {
    // 0 ~ i 做到有序
			// j + 1就是i
			// arr[j] > arr[j + 1]	就是两数相等也不交换。若为 >=，则两数相等也交换，这是多此一举！
			for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
   
				swap(arr, j, j + 1);
			}
		}
	}

	// i和j是一个位置的话，会出错
	public static void swap(int[] arr, int i, int j) {
   
		arr[i] = arr[i] ^ arr[j];
		arr[j] = arr[i] ^ arr[j];
		arr[i] = arr[i] ^ arr[j];
	}

	// for test
	public static void comparator(int[] arr) {
   
		Arrays.sort(arr);
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
   
		// Math.random() -> [0,1) 所有的小数，等概率返回一个
		// Math.random() * N -> [0,N) 所有小数，等概率返回一个
		// (int)(Math.random() * N) -> [0,N-1] 所有的整数，等概率返回一个
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())]; // 长度随机
		for (int i = 0; i < arr.length; i++) {
   
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
   
		if (arr == null) {
   
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
   
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
   
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
   
			return false;
		}
		if (arr1 == null && arr2 == null) {
   
			return true;
		}
		if (arr1.length != arr2.length) {
   
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
   
			if (arr1[i] != arr2[i]) {
   
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
   
		if (arr == null) {
   
			return;
		}
		for (int i = 0; i < arr.length; i++) {
   
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
   
		int testTime = 500000;
		int maxSize = 100; // 随机数组的长度0～100
		int maxValue = 100;// 值：-100～100
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
   
			int[] arr = generateRandomArray(maxSize, maxValue);
			int[] arr1 = copyArray(arr);
			int[] arr2 = copyArray(arr);
			insertionSort(arr1);
			comparator(arr2);
			if (!isEqual(arr1, arr2)) {
   
				// 打印arr1
				// 打印arr2
				succeed = false;
				for (int j = 0; j < arr.length; j++) {
   
					System.out.print(arr[j] + " ");
				}
				System.out.println();
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		insertionSort(arr);
		printArray(arr);
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143

7.如何确定算法流程的总操作数量与样本数量之间的表达式关系

1. 想象该算法流程所处理的数据状况,要按照最差情况来。
2. 把整个流程彻底拆分为一个个基本动作,保证每个动作都是常
   数时间的操作。
3. 如果数据量为N,看看基本动作的数量和N是什么关系。

O为最差时间复杂度写法。上面第一个是最好时间复杂度写法；第二个是平均时间复杂度写法；第三个是最差时间复杂度写法。

8.注意

1. 算法的过程和具体的语言是无关的。
2. 想分析一个算法流程的时间复杂度的前提，是对该流程非常熟悉。
3. 一定要确保在折分算法流程时，拆分出来的所有行为都是常数时间的操作。这意味着你写算法时对自己的用过的每一个系统api，都非常的熟悉。否则会影响你对时间复杂度的估算。

9.额外空间复杂度

​​​​​​​​​​​​​​​你要实现一个算法流程，在实现算法流程的过程中，你需要开辟一些空间来支持你的算法流程。
作为输入参数的空间，不算额外空间。
作为输出结果的空间，也不算额外空间。
因为这些都是必要的、和现实目标有关的。所以都不算。
但除此之外，你的流程如果还需要开辟空间才能让你的流程继续下去。这部分空间就是额外空间。
如果你的流程只需要开辟有限几个变量,额外空间复杂度就是O(1)

O(1)：常数操作
流程中不需要开辟新的空间，有限几个变量就可以完成事情，额外空间复杂度就是O(1)
需要开辟额外数组，额外空间复杂度是O(N)。

额外空间的解释：和功能无关的必须申请的空间。

举例：给你一个数组arr，然后要求复制这个数组返回给用户，我们在流程中必须new一个新数组，然而这个数组是必须的，是被要求返回的，所以这个数组不属于额外空间。即作为输入参数的和输出结果的空间不算额外空间。
选择，冒泡，插入都是申请了有限几个变量，所以他们的额外空间复杂度都是O(1)

10.算法流程的常数项

我们会发现，时间复杂度这个指标，是忽略低阶项和所有常数系数的。
难道同样时间复杂度的流程，在实际运行时候就一样的好吗?

当然不是。

时间复杂度只是一个很重要的指标而已如果两个时间复杂度一样的算法,
你还要去在时间上拼优劣，就进入到拼常数时间的阶段,简称拼常数项。

算法流程的常数项的比拼方式：
放弃理论分析，生成随机数据直接测。
为什么不去理论分析?
不是不能纯分析，而是没必要。因为不同常数时间的操作，虽然都是固定时间，但还是有快慢之分的。
比如，位运算的常数时间原小于算术运算的常数时间，这两个运算的常数时间又远小于数组寻址的时间。
所以如果纯理论分析，往往会需要非常多的分析过程。都已经到了具体细节的程度，莫不如交给实验数据好了。

当时间复杂度相同时，就需要考虑常数项了，然而我们没必要进行理论分析，而是直接进行样本测试。因为当过程拆分到位时，每个基本的常数动作也是有时间快慢的。

±运算时间是比*/快的。±运算时间没有位运算快。

位运算符号：
| ：或

11.面试、比赛、刷题中，一个问题的最优解是什么意思？

一般情况下，认为解决一个问题的算法流程，在时间复杂度的指标上，一定要尽可能的低，先满足了时间复杂度最低这个指标之后，使用最少的空间的算法流程，叫这个问题的最优解。
一般说起最优解都是忽略掉常数项这个因素的，因为这个因素只决定了实现层次的优化和考虑，而和怎么解决整个问题的思想无关。

一般正规的比赛、面试是不考虑常数项时间的。

12.常见的时间复杂度

13.算法和数据结构学习的大脉络

（1）知道怎么算的算法
如：3+3=6

（2）知道怎么试的算法
如：暴力递归，之后寻求更优解

14.对数器

你在网上找到了某个公司的面试题，你想了好久，感觉自己会做，但是你找不到在线测试，你好心烦…
你和朋友交流面试题,你想了好久,感觉自己会做,但是你找不到在线测试，
你好心烦…
你在网上做笔试，但是前几个测试用例都过了，突然一个巨大无比数据量来了，结果你的代码报错了，如此大的数据量根本看不出哪错了，你好心烦…

对数器怎么用：
1.你想要测的方法a
2.实现复杂度不好但是容易实现的方法b
3.实现一个随机样本产生器
4.把方法a和方法b跑相同的随机样本看看得到的结果是否一样
5.如果有一个随机样本使得比对结果不一致，打印样本进行人工干预，改对
方法a和方法b
6.当样本数量很多时比对测试依然正确，可以确定方法a已经正确。

**举例：**选择排序的代码拿过来

package class01;

import java.util.Arrays;

public class Code01_SelectionSort {
   

	// 选择排序主方法
	public static void selectionSort(int[] arr) {
   
		if (arr == null || arr.length < 2) {
   
			return;
		}
		// 0 ~ N-1  找到最小值，在哪，放到0位置上
		// 1 ~ n-1  找到最小值，在哪，放到1 位置上
		// 2 ~ n-1  找到最小值，在哪，放到2 位置上
		for (int i = 0; i < arr.length - 1; i++) {
   
			int minIndex = i;
			for (int j = i + 1; j < arr.length; j++) {
    // i ~ N-1 上找最小值的下标 
				minIndex = arr[j] < arr[minIndex] ? j : minIndex;
			}
			swap(arr, i, minIndex);
		}
	}

	// 选择排序的交换数字方法
	public static void swap(int[] arr, int i, int j) {
   
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

	// 其他方法都是对数器的方法
	// for test
	public static void comparator(int[] arr) {
   
		Arrays.sort(arr);
	}

	// 产生随机数
	public static int[] generateRandomArray(int maxSize, int maxValue) {
   
		// Math.random()   [0,1)  
		// Math.random() * N  [0,N)
		// (int)(Math.random() * N)  [0, N-1]
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
   
			// [-? , +?]
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
   
		if (arr == null) {
   
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
   
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
   
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
   
			return false;
		}
		if (arr1 == null && arr2 == null) {
   
			return true;
		}
		if (arr1.length != arr2.length) {
   
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
   
			if (arr1[i] != arr2[i]) {
   
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
   
		if (arr == null) {
   
			return;
		}
		for (int i = 0; i < arr.length; i++) {
   
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
   
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
   
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			// 自己写的排序算法去排序一个数组
			selectionSort(arr1);
			// 系统的排序算法去排序一个数组
			comparator(arr2);
			// 如果两个数组相等，证明自己写的排序算法正确
			if (!isEqual(arr1, arr2)) {
   
				succeed = false;
				printArray(arr1);
				printArray(arr2);
				break;
			}
		}
		// 如果结果不正确，我们可以考虑把maxSize调小一点观察
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		selectionSort(arr);
		printArray(arr);
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146

15.认识二分法

经常见到的类型是在一个有序数组上，开展二分搜索。
但有序真的是所有问题求解时使用二分的必要条件吗?
不
只要能正确构建左右两侧的淘汰逻辑,你就可以二分。

使用场景：

（1）在一个有序数组中，找某个数是否存在
（2）在一个有序数组中，找>=某个数最左侧的位置
（3）在一个有序数组中，找<=某个数最右侧的位置
（4）局部最小值问题

举例：

（1）给定一个有序数组，寻找数组中的7是否存在。

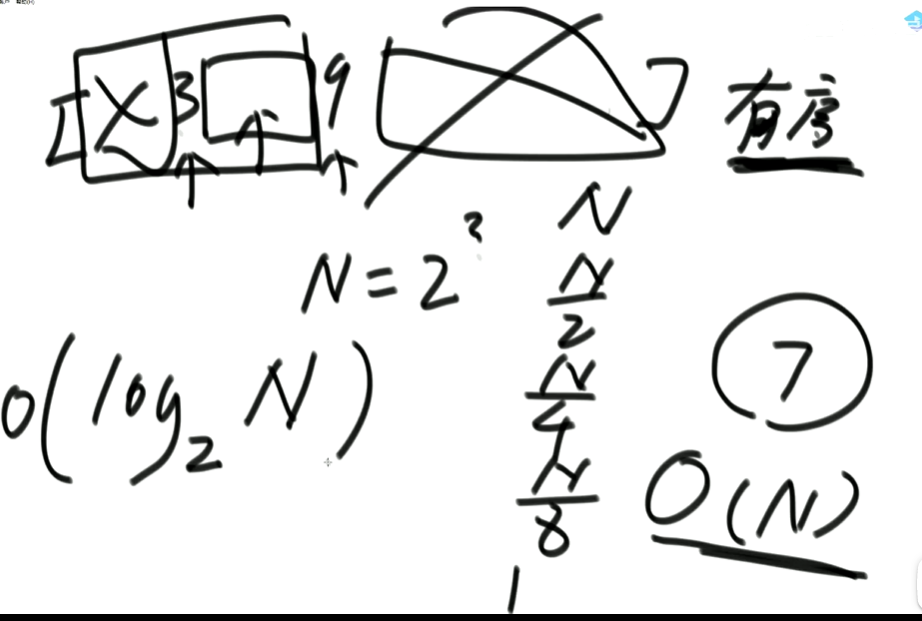
不断二分下，时间复杂度变化：N => 二分之N => 四分之N => 八分之N

因此，最后的时间复杂度是O(logN)

代码如下：

package class01;

import java.util.Arrays;

public class Code04_BSExist {
   

	public static boolean exist(int[] sortedArr, int num) {
   
		if (sortedArr == null || sortedArr.length == 0) {
   
			return false;
		}
		int L = 0;
		int R = sortedArr.length - 1;
		int mid = 0;
		// L..R
		while (L < R) {
    // L..R 至少两个数的时候
			// 若下方写成 mid = (L + R) / 2
			// L为10亿	R为18亿	L和R为下标
			// mid就溢出了，不安全！	安全可写成 mid = L + (R - L) / 2
			// 一个数N / 2 等价于	N >> 1 （N的二进制带符号右移1位）
			// 一个数N * 2 等价于	N << 1 （N的二进制带符号左移1位）
			// 一个数N * 2 + 1 等价于	((N << 1) | 1) （N的二进制带符号左移1位再或一下1， | 为或的意思）
			// 思考：N * 2 - 1 呢
			// 下方这么写是因为位运算比除运算快
			mid = L + ((R - L) >> 1);	// mid = (L + R) / 2
			if (sortedArr[mid] == num) {
   
				return true;
			} else if (sortedArr[mid] > num) {
   
				R = mid - 1;
			} else {
   
				L = mid + 1;
			}
		}
		return sortedArr[L] == num;
	}
	
	// for test
	public static boolean test(int[] sortedArr, int num) {
   
		for(int cur : sortedArr) {
   
			if(cur == num) {
   
				return true;
			}
		}
		return false;
	}
	
	
	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
   
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
   
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}
	
	public static void main(String[] args) {
   
		int testTime = 500000;
		int maxSize = 10;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
   
			int[] arr = generateRandomArray(maxSize, maxValue);
			Arrays.sort(arr);
			int value = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
			if (test(arr, value) != exist(arr, value)) {
   
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

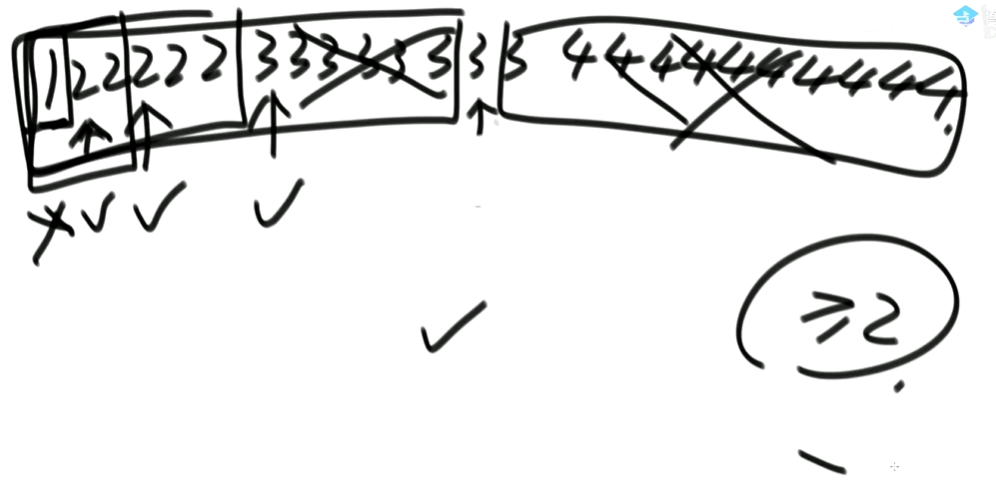
（2）给定一个有序数组，寻找>=2最左侧的位置

有序数组如下图：


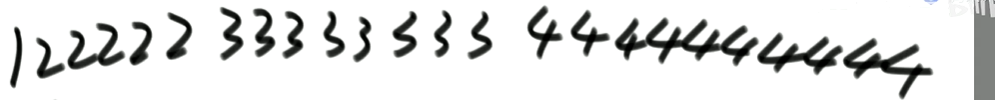
代码如下：

package class01;

import java.util.Arrays;

public class Code05_BSNearLeft {
   

	// 在arr上，找满足>=value的最左位置
	public static int nearestIndex(int[] arr, int value) {
   
		int L = 0;
		int R = arr.length - 1;
		int index = -1; // 记录最左的对号
		while (L <= R) {
    // 至少一个数的时候
			int mid = L + ((R - L) >> 1);
			if (arr[mid] >= value) {
   
				index = mid;
				R = mid - 1;
			} else {
   
				L = mid + 1;
			}
		}
		return index;
	}

	// for test
	public static int test(int[] arr, int value) {
   
		for (int i = 0; i < arr.length; i++) {
   
			if (arr[i] >= value) {
   
				return i;
			}
		}
		return -1;
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
   
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
   
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}
	
	// for test
	public static void printArray(int[] arr) {
   
		if (arr == null) {
   
			return;
		}
		for (int i = 0; i < arr.length; i++) {
   
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
   
		int testTime = 500000;
		int maxSize = 10;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
   
			int[] arr = generateRandomArray(maxSize, maxValue);
			Arrays.sort(arr);
			int value = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
			if (test(arr, value) != nearestIndex(arr, value)) {
   
				printArray(arr);
				System.out.println(value);
				System.out.println(test(arr, value));
				System.out.println(nearestIndex(arr, value));
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91

（3）有序数组中，找<=某个数最右侧的位置

package class01;

import java.util.Arrays;

public class Code05_BSNearRight {
   

	// 在arr上，找满足<=value的最右位置
	public static int nearestIndex(int[] arr, int value) {
   
		int L = 0;
		int R = arr.length - 1;
		int index = -1; // 记录最右的对号
		while (L <= R) {
   
			int mid = L + ((R - L) >> 1);
			if (arr[mid] <= value) {
   
				index = mid;
				L = mid + 1;
			} else {
   
				R = mid - 1;
			}
		}
		return index;
	}

	// for test
	public static int test(int[] arr, int value) {
   
		for (int i = arr.length - 1; i >= 0; i--) {
   
			if (arr[i] <= value) {
   
				return i;
			}
		}
		return -1;
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
   
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
   
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static void printArray(int[] arr) {
   
		if (arr == null) {
   
			return;
		}
		for (int i = 0; i < arr.length; i++) {
   
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
   
		int testTime = 500000;
		int maxSize = 10;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
   
			int[] arr = generateRandomArray(maxSize, maxValue);
			Arrays.sort(arr);
			int value = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
			if (test(arr, value) != nearestIndex(arr, value)) {
   
				printArray(arr);
				System.out.println(value);
				System.out.println(test(arr, value));
				System.out.println(nearestIndex(arr, value));
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91

（4）局部最小值问题

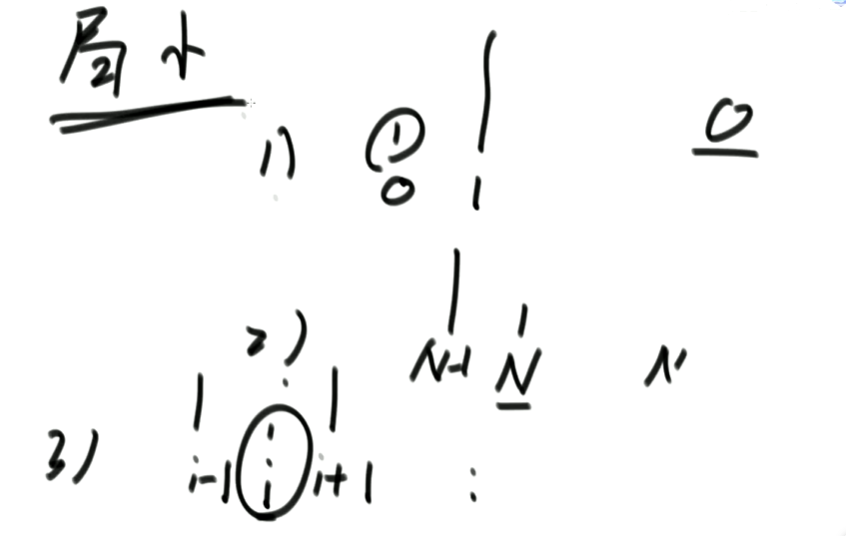
上图的解释：

对于0 1

0就是局部最小的位置，因为0的右边都比0大，且0的左边没数

对于2 1

1就是局部最小的位置，因为1的左边都比1大，且1的右边没数

对于i -1 i i+1

i

举例：一个无序数组arr，数组为arr[0…N-1]，相邻不相等，寻求局部最小值。

解法：可以考虑使用二分法。
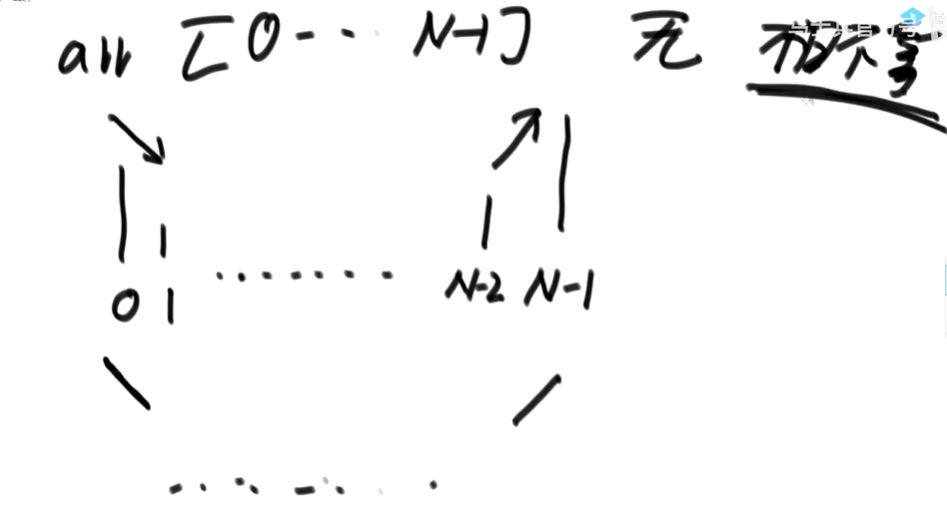
解析：

0位置和1位置比大小，N-2和N-1位置比大小。

若0位置<1位置，N-2位置小于N-1位置，则最小值一定在1位置到N-2位置中。我们再找0和N-1的中间位置，也就是进行二分，之后再二分。

二分法不一定要有序才能二分。

代码如下：

package class01;

public class Code06_BSAwesome {
   

	public static int getLessIndex(int[] arr) {
   
		if (arr == null || arr.length == 0) {
   
			return -1; // no exist
		}
		if (arr.length == 1 || arr[0] < arr[1]) {
   
			return 0;
		}
		if (arr[arr.length - 1] < arr[arr.length - 2]) {
   
			return arr.length - 1;
		}
		int left = 1;
		int right = arr.length - 2;
		int mid = 0;
		while (left < right) {
   
			mid = (left + right) / 2;
			if (arr[mid] > arr[mid - 1]) {
   
				right = mid - 1;
			} else if (arr[mid] > arr[mid + 1]) {
   
				left = mid + 1;
			} else {
   	// 这种情况即：arr[mid - 1] < arr[mid] < arr[mid + 1]。即局部最小值
				return mid;
			}
		}
		return left;
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

16.认识异或运算

异或运算：相同为0，不同为1。
同或运算：相同为1，不同为0。
能长时间记住的概率接近0。
所以，异或运算就记成无进位相加。

举例： 6 ^ 7 = ? （^是异或的意思）

6的二进制：110

7的二进制：111

6 ^ 7 =

110

^

111

=001

=1

异或运算就记成无进位相加

思考：做一个数学计算器，包括各种数学符号

异或运算的性质

（1）0 ^ N == N；N ^ N == 0
（2）异或运算满足交换律和结合率

上面的两个性质用无进位相加来理解就非常的容易

交换律和结合律举例：a ^ b ^ c == a ^ c ^ b

（1）题目一：如何不用额外变量交换两个数

举例：int a = 甲，int b = 乙 令 int a =乙，int b = 甲

解法：

提示： a = a ^ b 此行结束b的值不变
b = a ^ b 此行结束a的值不变
a = a^ b 此行结束完成要求

代码如下：

  		int a = 6;
		int b = -1000;
		
		System.out.println(a);
		System.out.println(b);
		
		
		a = a ^ b;
		b = a ^ b;
		a = a ^ b;

		System.out.println(a);
		System.out.println(b);
1
2
3
4
5
6
7
8
9
10
11
12
13

  // 交换arr的i和j位置上的值
	public static void swap(int[] arr, int i, int j) {
   
		arr[i] = arr[i] ^ arr[j];
		arr[j] = arr[i] ^ arr[j];
		arr[i] = arr[i] ^ arr[j];
	}
1
2
3
4
5
6
7

（2）注意

如果a,b相等也对，因为int型的a=b=6，但是它们的内存是两个东西，如下：

  		int a = 6;
		int b = 6;
		
		System.out.println(a);
		System.out.println(b);

		a = a ^ b;
		b = a ^ b;
		a = a ^ b;

		System.out.println(a);
		System.out.println(b);
1
2
3
4
5
6
7
8
9
10
11
12

下面的情况使用异或就错了：

	int[] arr = {
   3,1,100};

    System.out.println(arr[0]);
    System.out.println(arr[2]);
		
	swap(arr, 0, 0);    // 内存区域相同，这就错了
		
	System.out.println(arr[0]);
	System.out.println(arr[2]);
		
	
	public static void swap (int[] arr, int i, int j) {
   
		// arr[0] = arr[0] ^ arr[0];
		arr[i]  = arr[i] ^ arr[j];
		arr[j]  = arr[i] ^ arr[j];
		arr[i]  = arr[i] ^ arr[j];
	}
	
	
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

结论：值相同没关系，但内存必须不同。

（3）题目二：一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这个数。

解法：
int eor = 0; 然后把其中的所有数异或起来，eor结果就是出现奇数次的数。

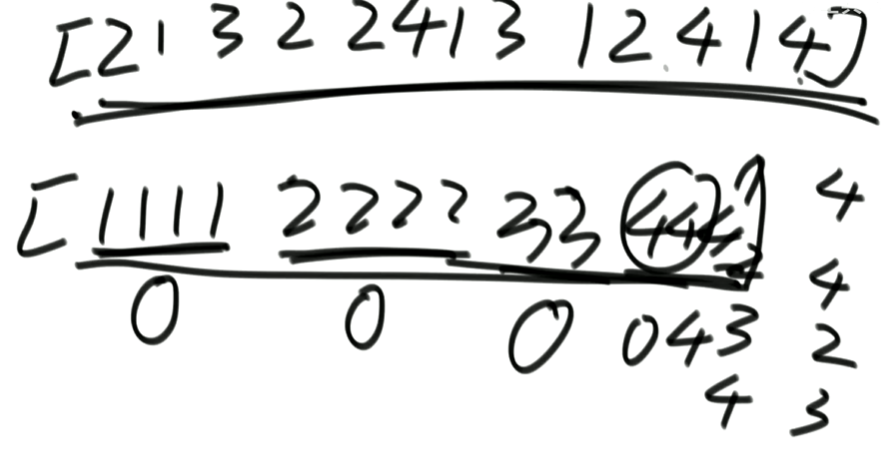
代码如下：

  	// arr中，只有一种数，出现奇数次
	public static void printOddTimesNum1(int[] arr) {
   
		int eor = 0;
		for (int i = 0; i < arr.length; i++) {
   
			eor ^= arr[i];
		}
		System.out.println(eor);
	}
1
2
3
4
5
6
7
8
9
10

（4）题目三：怎么把一个int类型的数，提取出最右侧的1来

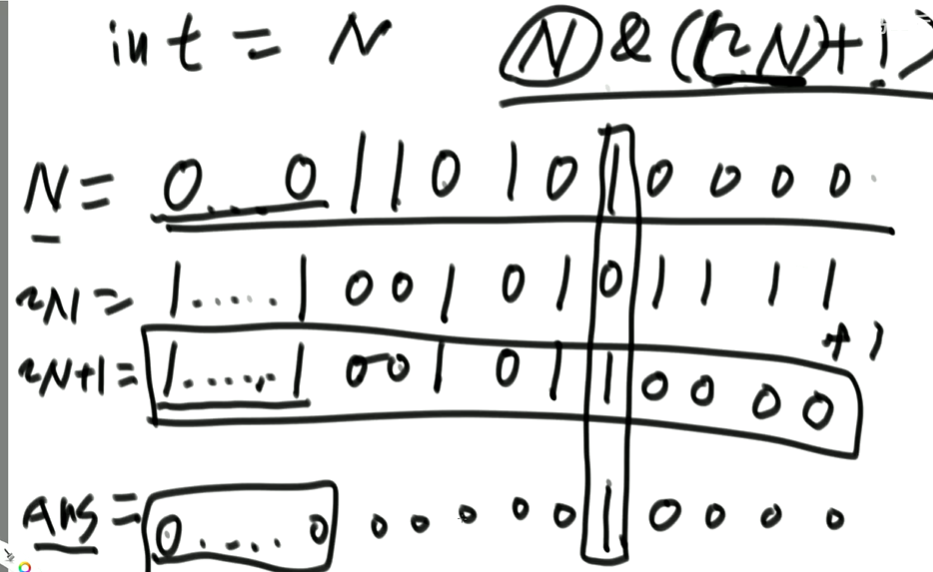
解法：N与上(N取反+1)

（5）题目四：一个数组中有两种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这两种数。

解法：创建变量 int eor = 0; 设a,b为出现奇数次的数，arr数组。eor异或arr数组中所有的数。

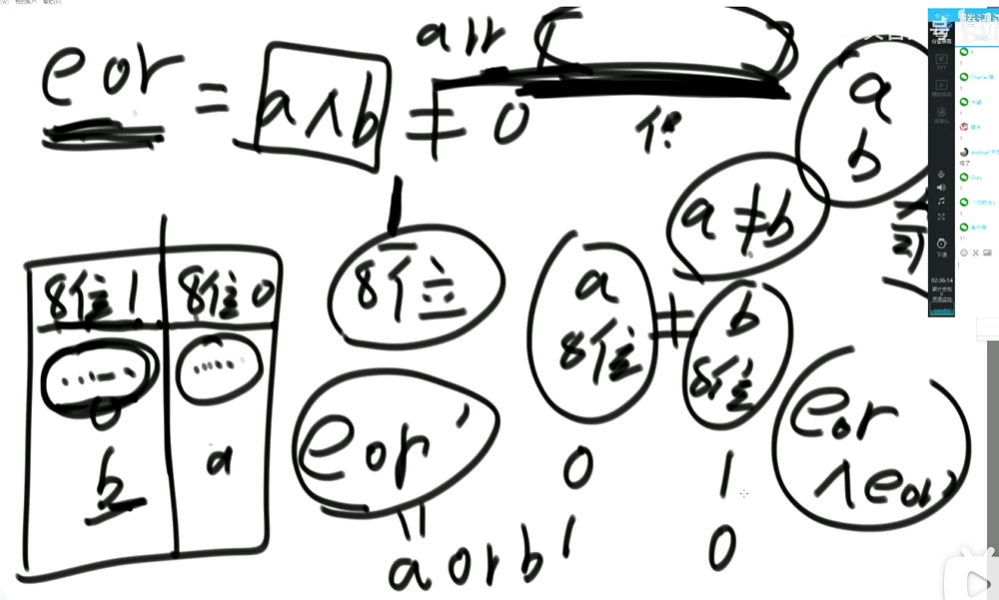
eor = a ^ b;且eor != 0。因为 N ^ N == 0，所以eor != 0 eor != 0 说明eor的二进制的某个位置上有1，假设第8位是1。则a的第8位和b的第8位是不一样的。此时我们从这个角度再次分类数组，一类数是第8位为0的，一类数是第8位为1的。

int eor’ = 0; eor ’ = eor’ ^ 所有第8位是0或1的数 此时的eor ’ = a 或 b

eor = eor ^ eor’ 此时的eor就是另外一个 即eor = b 或 a

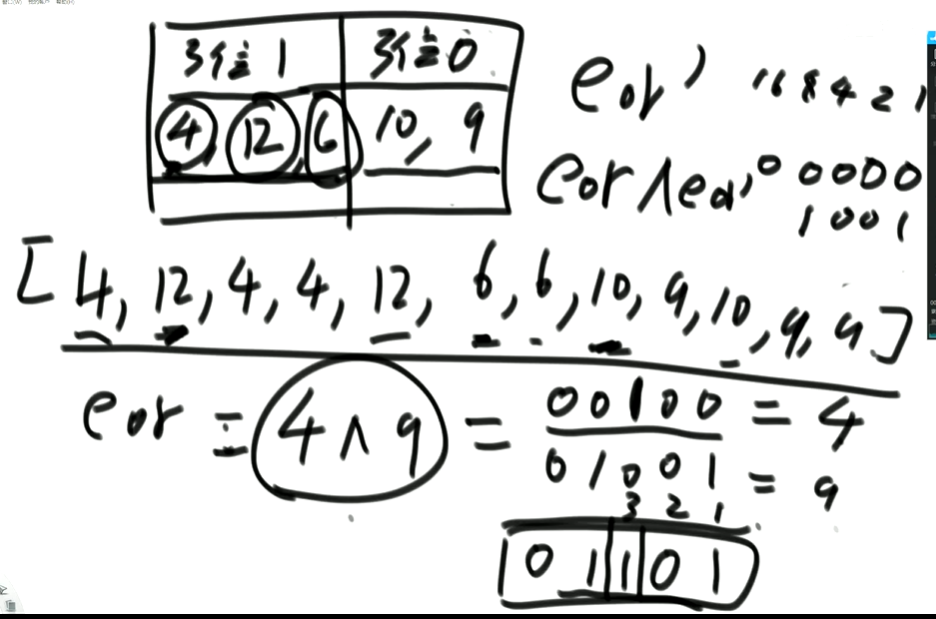
这里的第8位为1是假设的，我们找只需要找eor的最右侧的1。eor的二进制最右侧的1找法见上述的第（4）点。

这里也不一定非要选最右侧的1，只需要某一位上a和b不同即可。下图即为选中第三位的1：

代码如下：

	// arr中，有两种数，出现奇数次
	public static void printOddTimesNum2(int[] arr) {
   
		int eor = 0;
		for (int i = 0; i < arr.length; i++) {
   
			eor ^= arr[i];
		}
		// 上述代码结束后eor == a ^ b
		// a 和 b是两种数
		// eor != 0
		// eor最右侧的1，提取出来
		// eor :     00110010110111000
		// rightOne :00000000000001000
		int rightOne = eor & (~eor + 1); // 提取出最右的1 	int rightOne = eor & (-eor);这种写法好像也可以，好像！
		
		// int eor’ = 0; eor ’ = eor’ ^ 所有第8位是0或1的数 此时的eor ’ = a 或 b
		// eor = eor ^ eor’ 此时的eor就是另外一个 即eor = b 或 a
		int onlyOne = 0; // onlyOne就是eor'
		for (int i = 0 ; i < arr.length;i++) {
   
			//  arr[i] =  111100011110000
			// rightOne=  000000000010000
			if ((arr[i] & rightOne) != 0) {
   	// eor’ ^ 所有第8位是0或1的数
				onlyOne ^= arr[i];
			}
		}
		// 此时的eor ’ = a 或 b，即此时的onlyOne = a或b。	eor = eor ^ eor’ 
		// 此时的eor就是另外一个 即eor = b 或 a
		System.out.println(onlyOne + " " + (eor ^ onlyOne));
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

（6）题目五：输出二进制中1的个数

代码如下：

    // 数出二进制中1的个数
	public static int bit1counts(int N) {
   
		int count = 0;

		while(N != 0) {
   	//	初始数字N：011011010000
			int rightOne = N & ((~N) + 1);	//   rightOne = 000000010000     1  第一个1就提取出来了
			count++;
			N ^= rightOne;		//   N = 011011000000	这就把最右边的1也就是提取出来的第一个1抹掉了（异或是无进位相加）
			// N -= rightOne(N是负数这样写就错了，所以写成N ^= rightOne;)	// 之后不断抹去1，又有count ++ .抹掉一个1，count+1.这就数出来1的个数
		}

		return count;
		
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

二、链表结构、栈、队列、递归行为、哈希表和有序表

提示：程序员代码面试指南一书默认懂了所有的基础再看

1.单向链表

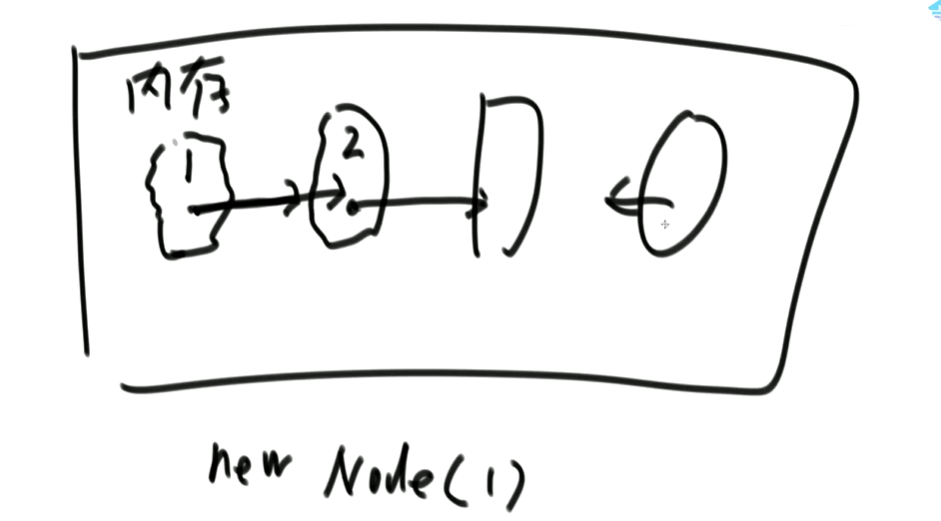
2.双向链表

3.单向链表和双向链表的最简单的练习

链表相关的问题几乎都是coding的问题。这里就是熟悉结构，链表还有哪些常见面试题，后续有专门一节来系统学习。

（1） 单向链表和双向链表如何反转

单向链表反转：

  public static class Node {
   
		public int value;
		public Node next;

		public Node(int data) {
   
			value = data;
		}
	}

    //  head
	//   a    ->   b    ->  c  ->  null
	//   c    ->   b    ->  a  ->  null
	public static Node reverseLinkedList(Node head) {
   
		Node pre = null;
		Node next = null;
		while (head != null) {
   
			next = head.next;    // next指针就是记录一下位置

			head.next = pre;
			pre = head;

			head = next;
		}
		return pre;
	}

    public static Node testReverseLinkedList(Node head) {
   
		if (head == null) {
   
			return null;
		}
		ArrayList<Node> list = new ArrayList<>();
		while (head != null) {
   
			list.add(head);
			head = head.next;
		}
		list.get(0).next = null;
		int N = list.size();
		for (int i = 1; i < N; i++) {
   
			list.get(i).next = list.get(i - 1);
		}
		return list.get(N - 1);
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

双向链表反转：

  public static class DoubleNode {
   
		public int value;
		public DoubleNode last;
		public DoubleNode next;

		public DoubleNode(int data) {
   
			value = data
1
2
3
4
5
6
7
8