【数据结构】时间复杂度和空间复杂度

时间复杂度： 快慢

空间复杂度：算法运行所需要的额外空间

时间复杂度

不是从秒数来算

一个算法运行时间和硬件配置有关，无法算出准确时间。

时间复杂度计算的是算法的执行次数，一个执行次数有可能多条语句，也有可能一条语句，但肯定是常数条语句。

void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
	 for (int j = 0; j < N ; ++ j)
	 {
			 ++count;
	 }
}
 
for (int k = 0; k < 2 * N ; ++ k)
{
	 ++count;
}
int M = 10;
while (M--)
{
	 ++count;
}
	printf("%d\n", count);
}

O(N^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

大O渐进表示法

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。
推导大O阶方法(计算它的数量级)：
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

// 计算Func2的时间复杂度？
void Func2(int N)
{
 int count = 0;
 for (int k = 0; k < 2 * N ; ++ k)
 {
	 ++count;
 }
 int M = 10;
 while (M--)
 {
	 ++count;
 }
 printf("%d\n", count);
}

O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

// 计算Func2的时间复杂度？
void Func2(int N)
{
 int count = 0;
 for (int k = 0; **k < 2 * N** ; ++ k)
 {
	 ++count;
 }
 int M = 10;
 while **(M--)**
 {
	 ++count;
 }
	 printf("%d\n", count);
}
}

不知道M和N的大小 O(N+M)
N远大于M  O(N)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

// 计算Func4的时间复杂度？
void Func4(int N)
{
 int count = 0;
 for (int k = 0; k < 100; ++ k)
 {
 ++count;
 }
 printf("%d\n", count);
}

O(1)
1
2
3
4
5
6
7
8
9
10
11
12

O(1)是表示常数次，而不是1次

// 计算strchr的时间复杂度？
const char * strchr ( const char * str, int character );

strchr就是字符串数组中查找一个字符
原理:
while(*str)
{
	if(*str == character)
{
	return str;
}
else
	++str
}
return null;

helloworld\0
查找h
查找d
算法时间复杂度分割
最好O(1) 最坏O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

时间复杂度一般关注最坏运行情况，底线思维。

// 计算BubbleSort的时间复杂度？
void BubbleSort(int* a, int n)
{
			 assert(a);
	 for (size_t end = n; end > 0; --end)
	 {
			 int exchange = 0;
	 for (size_t i = 1; i < end; ++i)
	 {
	 if (a[i-1] > a[i])
	 {
		 Swap(&a[i-1], &a[i]);
		 exchange = 1;
	 }
	 }
	 if (exchange == 0)
			 break;
	 }
}
O(N^2)

F（N） = N-1 + N-2 +N-3......
((N-1+1)*(N-1))/2
最好情况:O(N-1)-O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

依次比较交换

算时间复杂度不能去数循环 不一定准确！ 一定要看算法思想进行计算

// 计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x)
{
 assert(a);
 int begin = 0;
 int end = n-1;
 while (begin < end)
 {
 int mid = begin + ((end-begin)>>1);
 if (a[mid] < x)
	 begin = mid+1;
 else if (a[mid] > x)
	 end = mid;
 else
	 return mid;
 }
	 return -1;
}
O(logN)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

不断二分找，缩短一半 缩短一半

可以拿一张纸实验

最好O(1)

最坏O(logN)

N/2/2/2/2/2……/2 = 1

折半了多少次就除了多少个2

假设查找了X次

2^x = N

所以x = logN

因为要在文本中写对数不好写，而时间复杂度中，log2N 经常出现，所以我们会把它简写成logN,去掉底数。

O(N) O(logN) 对比 差距很大！

1000 10

100W 20

10亿 30

先分析是否符合要求 N次

• 思路1（映射）

  O(N) 使用了额外的空间 空间复杂度O(N)

  开辟（malloc）一个额外N+1个数的数组
  

  值都初始化成-1

  遍历这些数字，这个数是多少，就写到数组的对应位置

遍历一遍数组，哪个位置是 - 1 ，这个位置的下标就是缺失的数字。

0-N   求和公式计算 然后减

{0，5，4，2，6，3}
1
2
3
4
5

• 思路2 异或

  用一个x = 0,x跟数组中这些数据都异或一遍，然后再跟0-N+1之间的数字异或一遍，最后X才是缺失的数字。

  利用异或的特性，res = res ^ x ^ x。对同一个值异或两次，那么结果等于它本身，所以我们对res从0-nums.length进行异或，同时对nums数组中的值进行异或**，出现重复的会消失，所以最后res的值是只出现一次的数字**，也就是nums数组中缺失的那个数字。

  异或不需要考虑顺序

  X = 0
  

  其他数出现两次，只有缺失的那个数出现一次。
  

  数组 6 个，总共7个数 因为缺一个

  异或练习 二进制位（同为0，异为1）

  异或运算满足交换律，

**两个相同的数异或后值为0，0与任何数异或后值为这个数本身。**
1

X = 0                    0和2异或是2 ，0和3 0和3  3消失了

记住 相当于拿到前面 

x = x ^ arr[i] 每一个计算结果拿到前面去再和下一个数异或

2 3 3 4 4      结果是2

X=0       结果是2

3 2 4 3 4
1
2
3
4
5
6
7
8
9
10
11

• 思路3：排序+二分查找

  冒泡 O（N^2）

• 思路4：公式计算

  求和公式计算

  0-N

  {0，2，5，3，6，4}

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{
 if(N == 0)
 return 1;
 
 return Fac(N-1)*N;
}
O(N)
1
2
3
4
5
6
7
8
9

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

O(2^N)
1
2
3
4
5
6
7
8
9
10

右边先结束，缺一点 所以减去常数个，影响也不大。

//对比O(N)和O(2^N)
long long Fib(size_t N) //没有实际意义，太大了
{
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

long long Fac(size_t N)
{
 if(N == 0)
 return 1;
 
 return Fac(N-1)*N;
}
int main()
{
	printf("%lld",Fac(100));
	printf("%lld",Fib(100));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

fib递归改循环以后，时间复杂度O(N)

效率提高

空间复杂度

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{
 assert(a);//绿色为开的额外空间一共4个
 for (size_t **end** = n; end > 0; --end)
 {
 int **exchange** = 0;
 for (**size_t i** = 1; i < end; ++i)
 {
 if (a[i-1] > a[i])
 {
 **Swap(&a[i-1], &a[i]);**
 exchange = 1;
 }
 }
 if (exchange == 0)
 break;
 }
}

O(1) **空间不累积**
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的**前n项**
long long* Fibonacci(size_t n)
{
 if(n==0)
 return NULL;
 
 ***long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));***
 fibArray[0] = 0;
 fibArray[1] = 1;
 for (int i = 2; i <= n ; ++i)
 {
 fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
 }
 return fibArray;
}

O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

按照思想算复杂度，思想！

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
 if(N == 0)
 return 1;
 
 return Fac(N-1)*N;
}

O(N)
1
2
3
4
5
6
7
8
9
10

递归函数建立栈帧 ，函数里放的返回值参数等等

// 计算斐波那契递归Fib的空间复杂度？
long long Fib(size_t N)
{
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}
O(N)   空间不累计 2+4+....+N
1
2
3
4
5
6
7
8
9

先调用N-1这条路，递归完了往回走，再递归 就是一条线下去的，最底下空间直接销毁了，空间还用原来的。空间不累计。左边销毁了 右边开始还是用的左边的空间

空间不累计，可以重复利用！

//空间可以重复利用例子
void f1()
{
	int a = 0;
	printf("%p",a);
}
void f2()
{
	int a = 0;
	printf("%p",a);
}
int main()
{
	f1();
	f2();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

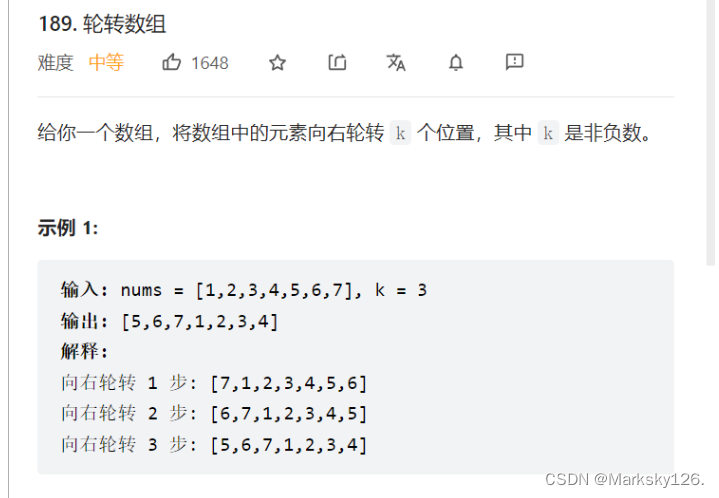
要求：时间复杂度为O(N)

最后一个数拿出来，前面的数往后挪

思路1：

tmp保存最后一个数，前n-1个数往后挪，再把7拿到前面去，在外面套一次循环，循环k次。

每次旋转1次，旋转k次

空间复杂度:O(1)
时间复杂度：O(N*k)

          其实就是N^2
1

思路2：

以空间换时间

因为是对原数组，所以要拷回去。

时间复杂度O(2N)

空间复杂度O(N)

考虑k>n,需mod一下 因为等于k

思路3：(三次逆置) 满足要求

前n-k逆置

后k个逆置

整体逆置

逆置其实就是头尾两个指针，然后交换，然后加减指针，走就行了

记得Mod