【HDU No. 1043】 八数码 Eight

【HDU No. 1043】 八数码 Eight

杭电OJ 题目地址

【题意】

十五数码问题是由15块滑动的方块构成的，在每一块上都有一个1～15的数字，所有方块都是一个4×4的排列，其中一块方块丢失，称之为“x”。

拼图的目的是排列方块，使其按以下顺序排列：

其中唯一合法的操作是将“x”与相邻的方块之一交换。

下面的移动序列解决了一个稍微混乱的拼图：

上一行中的字母表示在每个步骤中“x”方块的哪个邻居与“x”交换；合法值分别为“r”“l”“u”和“d”，表示右、左、上和下。

在这个问题中，编写一个程序来解决八数码问题，它由3×3的排列组成。

【输入输出】

输入：

输入包含多个测试用例，描述是初始位置的方块列表，从上到下列出行，在一行中从左到右列出方块，其中的方块由数字1～8加上“x”表示。例如以下拼图

由以下列表描述：

输出：

如果没有答案，则输出“unsolvable”，否则输出由字母“r”“l”“u”和“d”组成的字符串，描述产生答案的一系列移动。字符串不应包含空格，并从行首开始。

【样例】

【思路分析】

本题为八数码问题，包含多个测试用例，同一题目的POJ1077数据弱，只有1个测试用例。要求通过x方块上下左右四个方向移动，经过最少的步数达到目标状态。例如，初始状态1 2 3 x 4 6 7 5 8，经过r、d、r等3步后达到目标状态。

三种做法：答案不唯一
可以采用A算法、IDA算法或打表解决。

【1】 A* 算法

本题采用康托展开判断重复状态，以当前状态和目标状态的曼哈顿距离作为启发函数，评估函数为已走过的步数+启发函数，评估函数值越小越优先。

从初始状态开始，根据优先队列广度优先搜索目标状态。

① 预处理

首先将字符串读入，例如，1 2 3 x 4 6 7 5 8，将x 转换为数字8，其他字符1～8转换成数字0～7。转换之后的棋盘如下图所示。

用start.x 记录x 所在位置的下标，方便以后移动。

② 可解性判断

把除x外的所有数字排成一个序列，求序列的逆序对数。逆序对数指对于第i 个数，后面有多少个数比它小。例如，对于1 2 3 x 4 6 75 8，6后面有一个数5比它小，6和5是一个逆序对，7后面有一个数5比它小，7和5是一个逆序对，该序列共两个逆序对。数码问题可以被看作N ×N 的棋盘，八数码问题N =3，十五数码问题N =4。对于每一次交换操作，左右交换都不改变逆序对数，上下交换时逆序对数增加(N-1)、减少(N -1)或不变。

• N 为奇数时：上下交换时每次增加或减少的逆序对数都为偶数，因此每次移动逆序对数，奇偶性不变。若初态的逆序对数与目标状态的逆序对数的奇偶性相同，则有解。
• N 为偶数时：上下交换时每次增加或减少的逆序对数都为奇数，上下交换一次，奇偶性改变一次。因此需要计算初态和目标状态x相差的行数k ，若初态的逆序对数加上k 与目标状态逆序对数奇偶性相同，则有解。

八数码问题N =3，若初态的逆序对数与目标状态逆序对数奇偶性相同，则有解。本题目标状态的逆序对数为0，因此初态的逆序对数必须为偶数才有解。注意：统计逆序对数时x除外。

[算法代码]

bool check(node s){ //判断是否 有解【初态的逆序对数 为偶数】
	
	int cnt = 0;
	for(int i = 0 ; i < 9 ; i++){
		
		if(s.a[i] == 8){
			continue;
		}
		for(int j = i + 1; j < 9 ; j ++){
			if(s.a[j] < s.a[i] ){
				cnt ++;
			}
		}
	}
	if(cnt % 2){
		return 0;
	}
	return 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

③ 康托展开判重

在A*算法中，每种状态只需在第一次取出时扩展一次。如何判断这种状态已经扩展过了呢？可以设置哈希函数或使用STL中的map、set等方法。有一个很好的哈希方法是“康托（Cantor）展开”，它可以将每种状态都与0～(9!-1)的整数建立一一映射，快速判断一种状态是否已扩展。状态是数字0～8的全排列，共362 880个。将所有排列都按照从小到大的顺序映射到一个整数（位序），将排列最小的数012345678映射到0，将排列最大的数876543210映射到362880-1，如下图所示。

如果采用排序算法，则最快O (n !log(n !))，其中n =9。而康托展开可以在O (n^2 )时间内将一种状态映射到这个整数。康托展开是怎么计算的呢？例如，2031，求其在{0,1,2,3}全排列中的位序，其实就是计算排在2031前面的排列有多少个，可以按位统计，如下所述。

• 第0位的数字2：在2031中，2后面比2小的有两个数字{0,1}。以0开头，其他3个数字全排列有3!个，即(0123,0132,0213,0231,0312,0321)；以1开头，其他3个数字全排列有3!个(1023,1032,1203,1230,1302,1320)。因此排在以2开头的数字之前共2×3!个数字。
• 第1位的数字0：在2031中，0后面没有比0小的数字。
• 第2位的数字3：在2031中，3后面比3小的有1个数字{1}，前两位20确定，以1开头，剩余1个数字的全排列有1!个数字，即2013。排在3之前的共1×1!个数字。
• 第3位的数字1：在2031中，1后面没有比它小的数字。

因此2031的位序为2×3!+1=13。

位序计算公式：

其中，cnt[i ]为a [i ]后面比a [i ]小的数字个数，n 为数字个数。

8数码问题包含0～8共9个数字，首先求出0～8的阶乘并将其保存到数组中。然后统计在每一个数字后面有多少个数字比它小，累加cnt*fac[8-i ]即可得到该状态的位序。状态与位序之间是一一映射的，无须处理哈希冲突问题。

[算法代码]

fac[0] = 1;

for(int i = 1;  i < 9 ; i ++){
	fac[i] = fac[i - 1] * i;
}

int cantor(node s){ //康托判重
	
	int code = 0;
	for(int i = 0 ; i < 9  ;i ++){
		int cnt = 0 ;
		for(int j = j + 1; j < 9 ; j ++){
			if(s.a[j] < s.a[i]){
				cnt ++;
			}
		}
		code += cnt * fac[8 - i];
	}
	return code;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

④ 曼哈顿距离

A*算法的启发函数有多种设计方法，可以选择当前状态与目标状态位置不同的数字个数，也可以选择当前状态的逆序对数（目标状态逆序对数为0），还可以选择当前状态与目标状态的曼哈顿距离。本题选择当前状态和目标状态的曼哈顿距离作为启发函数。曼哈顿距离又被称为“出租车距离”，指行列差的绝对值之和，即从一个位置到另一个位置的最短距离。例如，从A点到B点，无论是先走行后走列，还是先走列后走行，走的距离都为行列差的绝对值之和。如下图所示，A和B的曼哈顿距离为2+1=3。

求当前状态与目标状态的曼哈顿距离，需要将两种状态上的数字位置转换为行、列，然后求行、列差的绝对值之和。例如，当前状态和目标状态如下图所示，将位置下标i 转换为行(i /3)，转换为列(i %3)。当前状态的数字4的位置下标为7，转换为7/3行、7%3列，即2行、1列。目标状态的数字4的位置下标为4，转换为4/3行、4%3列，即1行、1列。两个位置的曼哈顿距离为|2-1|+|1-1|=1。

除了8（x滑块），计算当前状态和目标状态中每个位置的曼哈顿距离之和。曼哈顿距离为什么不需要计算8（x滑块）？因为其他数字都是通过和滑块交换达到目标状态的。例如下图中，当前状态只有数字7，与目标状态的数字7位置不同，差一个曼哈顿距离，与滑块交换一次，7即可归位。当所有数字都与目标状态的位置相同时，滑块自然跑到了它应该在的位置。如果计算8（x滑块）的曼哈顿距离，那么当前状态和目标状态的曼哈顿距离为2，很明显是错误的，进行一步交换就可以达到目标状态。

[算法代码]

int h(node s){ // 启发函数，曼哈顿距离【行列差 的绝对值之和】
	int cost = 0;
	
	for(int i = 0 ; i < 9 ; i ++){
		if(s.a[i] != 8){
			cost += abs(i / 3 - s.a[i] / 3) + abs(i % 3 - s.a[i] % 3)	
		}
	}
	return cost;
}
1
2
3
4
5
6
7
8
9
10

⑤ A* 算法

[算法步骤]

(1) 创建一个优先队列，将评估函数f (t )=g (t )+h (t )作为优先队列的优先级，g (t )为已走过的步数，h (t )为当前状态与目标状态的曼哈顿距离，f (t )越小越优先。计算初始状态的启发函数h(start)，计算初始状态的康托展开值cantor(start)并标记已访问，初始状态入队。

(2) 如果队列不空，则队头t 出队，否则算法结束。

(3) 计算康托展开值k_s=cantor(t )，从t 出发向4个方向扩展。

计算x 新位置 的行列值：

int row = t.x / 3 + dir[i][0]; //行
int col = t.x % 3 + dir[i][1]; //列

int newx = row * 3 + col; //转换为下标
1
2
3
4

例如，如下图所示，当前状态x（数字8）的位置t .x=3，将其转换为 3/3=1行、3%3=0列，向右移动一格后，x的新位置为1行、1列，转换为下标为4。

如果新位置超出边界，则继续下一循环，否则令新旧位置上的数字交换，记录新状态x的位置。计算新状态的评估函数，nex.g++;nex.h=h(nex); ex.f=nex.g+nex.h; 计算新状态的康托展开值k_n=cantor(nex)，如果该状态已被访问，则继续下一循环；否则标记已访问，并将新状态入队。

pre[k_n] = k_s; //记录新状态的前驱，康托展开值唯一 标识该状态
ans[k_n] = to_c[i]; //记录移动方向字符
1
2

如果k_n=0，则说明已找到目标（目标状态康托展开值为0），返回。

[算法代码]

#include//A* 算法
#include
#include
#include
#include
#include
using namespace std;
const int N=362880+10;
const int dir[4][2]={1,0,0,1,-1,0,0,-1};
const char to_c[]="drul";
struct node{
    int f,g,h;
    int x;//'x'的位置 
    int a[9];
    bool operator < (const node &a) const{
        return f>a.f;
    }
};
node start,nex;
int fac[10],vis[N],pre[N];
char ans[N];

bool check(node s){//判断是否有解 
    int cnt=0;
    for(int i=0;i<9;i++){
    	if(s.a[i]==8) continue;
    	for(int j=i+1;j<9;j++)
			if(s.a[j]<s.a[i]) cnt++;
	}
    if(cnt%2) return 0;
    return 1; 
}

int cantor(node s){//康托判重 
    int code=0;
    for(int i=0;i<9;i++){
        int cnt=0;
        for(int j=i+1;j<9;j++)
			if(s.a[j]<s.a[i]) cnt++;
        code+=fac[8-i]*cnt;
    }
    return code;
}

int h(node s){//启发函数，曼哈顿距离（行列差绝对值之和） 
	int cost=0;
	for(int i=0;i<9;i++){
		if(s.a[i]!=8)
			cost+=abs(i/3-s.a[i]/3)+abs(i%3-s.a[i]%3);
	}
	return cost;
}

void Astar(){
    int k_s,k_n;
    priority_queue<node>q;
    while(!q.empty()) q.pop();
    memset(vis,0,sizeof(vis));
    start.g=0;start.f=start.h=h(start);
    vis[cantor(start)]=1;
    q.push(start);
    while(!q.empty()){
        node t=q.top();
        q.pop();
        k_s=cantor(t);
        for(int i=0;i<4;i++){
        	nex=t;
            int row=t.x/3+dir[i][0];
			int col=t.x%3+dir[i][1];
			int newx=row*3+col;//转换为数字 
			if(row<0||row>2||col<0||col>2) continue;
            swap(nex.a[t.x],nex.a[newx]);
            nex.x=newx;
            nex.g++;
			nex.h=h(nex);
            nex.f=nex.g+nex.h;
            k_n=cantor(nex);
            if(vis[k_n]) continue;
            vis[k_n]=1;
            q.push(nex);
            pre[k_n]=k_s;
            ans[k_n]=to_c[i];
            if(k_n==0) return;
        }  
    }
    return;
}

int main(){
    int judge,now;
    fac[0]=1;
    for(int i=1;i<9;i++) fac[i]=fac[i-1]*i;
    while(~scanf("%s",ans)){
		if(ans[0]>'0'&&ans[0]<'9')
			start.a[0]=ans[0]-'0'-1;
		else if(ans[0]=='x')
			start.x=0,start.a[0]=8;
		for(int i=1;i<9;i++){
			scanf("%s",ans);
			if(ans[0]>'0'&&ans[0]<'9')
				start.a[i]=ans[0]-'0'-1;
			else if(ans[0]=='x')
				start.x=i,start.a[i]=8;
		}
        if(!check(start)) {printf("unsolvable\n"); continue;}
        judge=cantor(start);
		now=0;
        Astar(); 
        stack<int>s;
        while(judge!=now){
            s.push(ans[now]);
            now=pre[now];
        }
        while(!s.empty()){
            printf("%c",s.top());
            s.pop();
        }
        printf("\n");
    }
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122

OK，这是A* 算法 的实现方式

【2】 IDA* 算法

IDA*算法是带有评估函数的迭代加深DFS算法，本题设计评估函数f(t )=g (t )+h (t )，g (t )为已走过的步数，h (t )为当前状态与目标状态的曼哈顿距离。

[算法步骤]

(1) 从depth=1开始进行深度优先搜索。

(2) 计算当前状态与目标状态的曼哈顿距离t =h ()，如果t =0，则说明已找到目标，ans[d ]=‘\0’，返回1。如果d +t ＞depth，则返回0。

(3) 从当前状态出发，沿4个方向扩展。

(4) 如果没有找到目标，则增加深度，++depth，继续搜索。

[算法代码]

bool dfs(int x, int d, int pre){
	
	int t = h();
	if(!t){
		ans[d] = '\0';
		return 1;
	}
	if(d + t > depth){
		return 0;
	}
	for(int i = 0 ; i < 4 ; i ++){
		int row = x / 3 + dir[i][0];
		int col = x % 3 + dir[i][1];

		int newx = row * 3 + col; //转换为数字
		if(row < 0 || row > 2 || col < 0 || col > 2 || newx == pre){
			continue;	
		}
		swap(a[newx] , a[x]);
		ans[d] = str[i];
	
		if(dfs(newx , d + 1, x)){
			return 1;
		}
		swap(a[newx] , a[x]);
	}
	return 0;
}

void IDAstar(int x){
	depth = 0;
	while(++ depth){
		if(dfs(x , 0 , -1)){
			break;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

IDA算法优化算法： 上面的IDA算法深度从1开始，每次都增加1，这样搜索的速度不快。其实可以从初始状态到目标状态的曼哈顿距离开始，每次都增加上一次搜索失败的最小深度，从而提高搜索效率。HDU1043的提交运行时间在优化前为202ms，在优化后为124ms。

[算法步骤]

(1) 从depth=h()开始进行深度优先搜索。

(2) 计算当前状态与目标状态的曼哈顿距离t =h ()，如果t =0，则说明已找到目标，ans[d ]=‘\0’，返回1。如果d +t ＞depth，则更新mindep=min(mindep,d +t )，返回0。

(3) 从当前状态出发，沿着4个方向扩展。

(4) 如果没有找到目标，则增加深度，depth=mindep，继续搜索。

[算法代码]

bool dfs(int x, int d , int pre){
	
	int t = h();
	if(!t){
		ans[d] = '\0';
		return 1;
	}
	if(d + t > depth){
		mindep = min(mindep , d + t);
		return 0;
	}
	for(int i = 0 ; i < 4 ; i ++){
		
		int row = x / 3 + dir[i][0];
		int col = x % 3 + dir[i][1];
		
		int newx = row * 3 + col; //转换为数字
		if(row < 0 || row > 2 || col < 0  || col > 2 || newx == pre){
			continue;		
		}
		swap(a[newx] , a[x]);
		ans[d] = to_c[i];
		if(dfs(newx , d + 1 , x)){
			return 1;
		}
		swap(a[newx] , a[x]);
	}
	return 0;
}

void IDAstar(int x){
	
	depth = h();
	while(1){
		mindep = inf;
		if(dfs(x,  0 , -1)){
			break;
		}
		depth = mindep;
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

【3】 打表

打表是一种典型的用空间换时间的技巧，一般指将所有可能需要用到的结果都事先计算出来，在后面需要用到时可以直接查表。当所有的可能状态都不多时，用打表的办法速度更快。从目标状态开始进行广度优先搜索，反向搜索所有状态，记录该状态的前驱及方向字符。

记录方向字符时，因为是倒推的，所以左移相当于前一状态到目标状态的右移，因此方向字符为r，如下图所示。

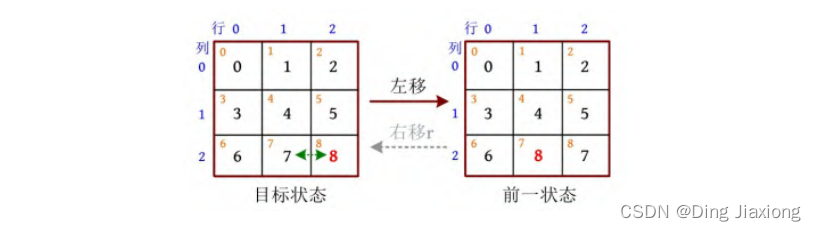
对每一个状态都用康托展开值作为唯一标识，如果求解从某一个状态到目标状态，则可以直接根据该状态的前驱数组找到目标状态。如果初始状态没被标记过，则说明从该状态无法到达目标状态。

[算法代码]

void get_all_result(){ //打表求解所有答案
	
	int k_s , k_n;
	memset(vis , 0 , sizeof(vis));
	for(int i = 0 ; i < 9 ; i++){
		st.a[i] = i;
	}
	st.x = 8;
	vis[cantor(st)] = 1;
	q.push(st);
	
	while(!q.empty()){
		node t = q.front();
		q.pop();
		k_s = cantor(t);
		
		for(int i = 0 ; i < 4 ; i ++){
			node nex = t;
			
			int row = t.x / 3 + dir[i][0];
			int col = t.x % 3 + dir[i][1];
				
			int newx = row * 3 + col; //转换为下标
			if(row < 0 || row > 2 || col < 0 || col > 2){
				continue;
			}
			nex.a[t.x] = t.a[newx];
			nex.a[newx] = 8;
			
			nex.x = newx;
			k_n = cantor(nex);
			if(vis[k_n]){
				continue;	
			}
			vis[k_n] = 1;
			q.push(nex);
			
			pre[k_n] = k_s;
			ans[k_n] = to_c[i];
		}
		
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

4种算法的运行时间及空间比较如下表所示。