二叉树的概念和性质

概念

 

● 二叉树是有限的节点集合------递归定义

        • 这个集合或者是空

        • 或者由一个根节点和两棵互不相交的称为左子树和右子树的二叉树组成

---

注意 : 二叉树的最大度数是2 , 是因为节点的两个后继孩子, 分为左孩子和右孩子 , 所以才成二叉树 .

● 五种基本形态

 性质2

● 性质

     • 非空二叉树上第 i 层上至多有 2^(i - 1) 个节点 (i >=1)

● 证明

      • 由树的性质2 可推出

      • 度为m 的树 , 因为 每个节点 , 最多有 m 个孩子 , 所以第 i 层 最多有 m^(i - 1) 个节点. 

---

第一层 有  m^0 个节点

第二层有   m^(2-1)个节点

……

第 i  层最多有 m^(i - 1) 个节点

性质 3

● 性质:

        • 高度为 h 的二叉树至多有 2^(h -1) 个节点 ( h >= 1)

● 证明:

        • 由树的性质 3 可推出

        • 高度为 h 的 m 次树 , 至多有 ( m^h -1 )/ (m-1)个节点

---

二叉树第一层最多有  2^0  个节点

第二层最多有       2^1

第三层                 2^(3-1)个

第四层                 2^(4-1)个

……

第 h 层                2^(h-1) 个 

所以 , 高度为 h 的二叉树 ,最多的节点数为:

Sn      =   2^0 +2^1+……+ 2^（h-1） ①

利用错位相减法 , 

2 Sn    =   2^1+ 2^2+……+2^h             ②

      ② - ① , 得  Sn =  2^(h -1)

满二叉树

●定义

         在一棵二叉树中 ,如果所有分支节点都有左孩子节点和右孩子节点,
        并且叶节点都集中在二叉树的最下层,这样的二叉树称为满二叉树.

 ● 特点

        • 叶子节点都在最下层

        • 只有度为 0 和度为 2 的节点

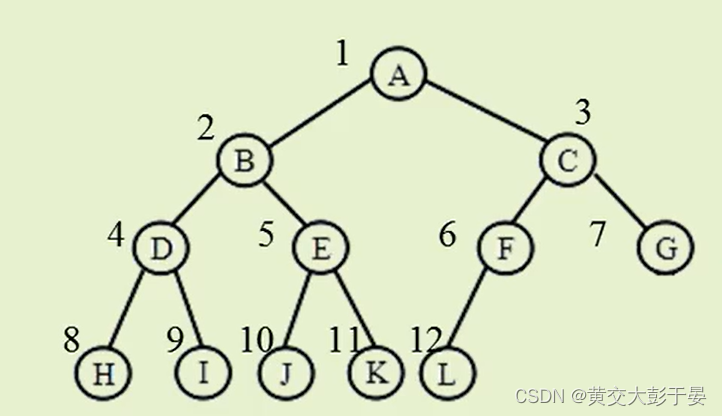
● 对满二叉树节点的连续编号: 树根为 1 , 按照层数从小到大、同一层从左到右的次序进行。

---

满二叉树节根据定义 ， 各个属性直接的关系：
● 一旦n 或 h 确定, 树形即确定
● 高度 h 以及 n₀、n₁  和 n₂(度分别为0,1,2的节点数)的关系有:
    • h  = log₂(n+1)    
        已知总节点数,求高度
    • n₁ = 0
        无度数为1的节点
    • n  = 2ʰ⁻1
        满二叉树的总个数
    • n₀ = 2ʰ⁻¹
        叶节点个数,即为第h层的满叶节点
    • n₂ = 2ʰ⁻¹-1
        度数为2的节点个数,即为前 (h-1)层节点总个数
● 满二叉树定义(另):
    • 一棵高为h,且有 2ʰ-1个节点的二叉树称为满二叉树     

完全二叉树

● 若二叉树中最多只有最下层的两层节点的度数可以小于 2 ， 并且最下面一层的叶节点都一次排列在该层最坐标的位置上 ， 则这样的二叉树称为完全二叉树

● 对满二叉树节点的连续编号 ：树根为 1 ， 按照层数从小到大、同一层从左到右的次序进行

---

注意 ： 完全二叉树 ， 相对于满二叉树 ， 只是最下层的叶子节点从右到左可以少几个（按顺序少的）

---

特点:

• 叶子节点只能在层次最大的两层上出现

• 最大层次上的叶子节点, 都依次排列在该层最左边的位置上

• 如果有度为 1 的节点 , 只能有一个, 且该节点只有左孩子 , 没有右孩子

• 按层编号后 , 一旦出现某节点(编号为 i ) 为叶子结点或只有左孩子 , 则编号大于 i  的节点 ,均为叶子节点

• 完全二叉树中一旦 n 确定, 其树形也确定看了 , 可以计算出高度 h 以及 n₀、n₁ 和 n₂, 其中n₁ =0或 1 , 当 n 为偶数时候 , n₁ =1, 当 n 为奇数时 , n₁ = 0.

另 : h= ⌊ log₂ n⌋ + 1 或 h = ⌈ log₂(n+1)⌉

性质 4

● 性质:

        对完全二叉树中编号为 i 的节点 (1 <= i <= n, n>=1 , n为节点数) :

  (1) 若 i <= ⌊ n/2⌋ , 即 2 i <= n , 则编号为 i 的节点为分支节点 ， 否则为叶子节点。

 

（2）若 n 为奇数 ， 则每个分支节点都即有左孩子节点 ， 也有右孩子节点 ；

若 n 为偶数 ， 则编号最大的分支节点只有左孩子节点，没有右孩子节点，其余分支节点都有左孩子、右孩子节点。

 

（3）编号为 i 的节点有左孩子节点，则左孩子节点的编号为 2i ; 若编号为 i 的节点有右孩子节点，则右孩子节点的编号为（2i + 1）。

 

（4）除数根节点外，若一个节点的编号为 i , 则它的双亲节点的编号为⌊ i/2 ⌋

       • 当 i 为 偶数时 ， 其双亲节点的编号为 i/2 , 它是双亲节点的左孩子

       • 当 i 为奇数时  ， 其双亲节点的编号为 （i-1/2）, 它是双亲节点的右孩子

性质 5

● 性质

具有 n 个（n>0）节点的完全二叉树的高度为⌈log₂（n+1）⌉ 或 ⌊log₂ n⌋+1

● 证明

● 设完全二叉树的高度为 h , 有

● 2ʰ⁻¹ -1 < n <= 2ʰ⁻1

● 即，2ʰ⁻¹ <= n <= 2ʰ

● 于是 : h-1 <= log₂ n < h

● 因为 h 是整数 , 故有结论

---