【二叉树层序遍历 + 置换环】逐层排序二叉树所需的最少操作数目

无论如何，请不要放弃，大家一起加油 ！ —— 2022/11/13

题目描述

给你一个 值互不相同 的二叉树的根节点 root 。在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。返回每一层按 严格递增顺序 排序所需的最少操作数目。节点的层数是该节点和根节点之间的路径的边数。

示例：

二、思路

本题可以分解下面两个小问题：

• 为层序遍历提取出每层所含的节点值
• 对每层节点值计算得到完全递增结果的需要的最小交换次数

二叉树的层序遍历方式这里不过多赘述，本文主要介绍如何通过置换环算法得到完成排序的最少置换元素次数 ——

置换环得到数组排序需要的最小交换次数

置换环的思想为 ： 对每个节点将其指向其排序后放到的位置，直到首位相接形成了一个环。

具体实现思想：

• 使用 Map 哈希表记录每个节点值以及其应该放到的位置
• 从头到尾遍历初始数组，使用 flag[] 数组标记当前元素是否已经参与过（即已经被加入环中），对已经参与过的数组元素则不再需要遍历。每次成环结束，记录成环个数 loop。
• 最终最小交换次数为 ：数组长度 - 成环个数 nums.size() - loop

以计算使得 [7, 6, 8, 5] 严格递增需要的最小交换次数为例，画出置换环算法图解如下：

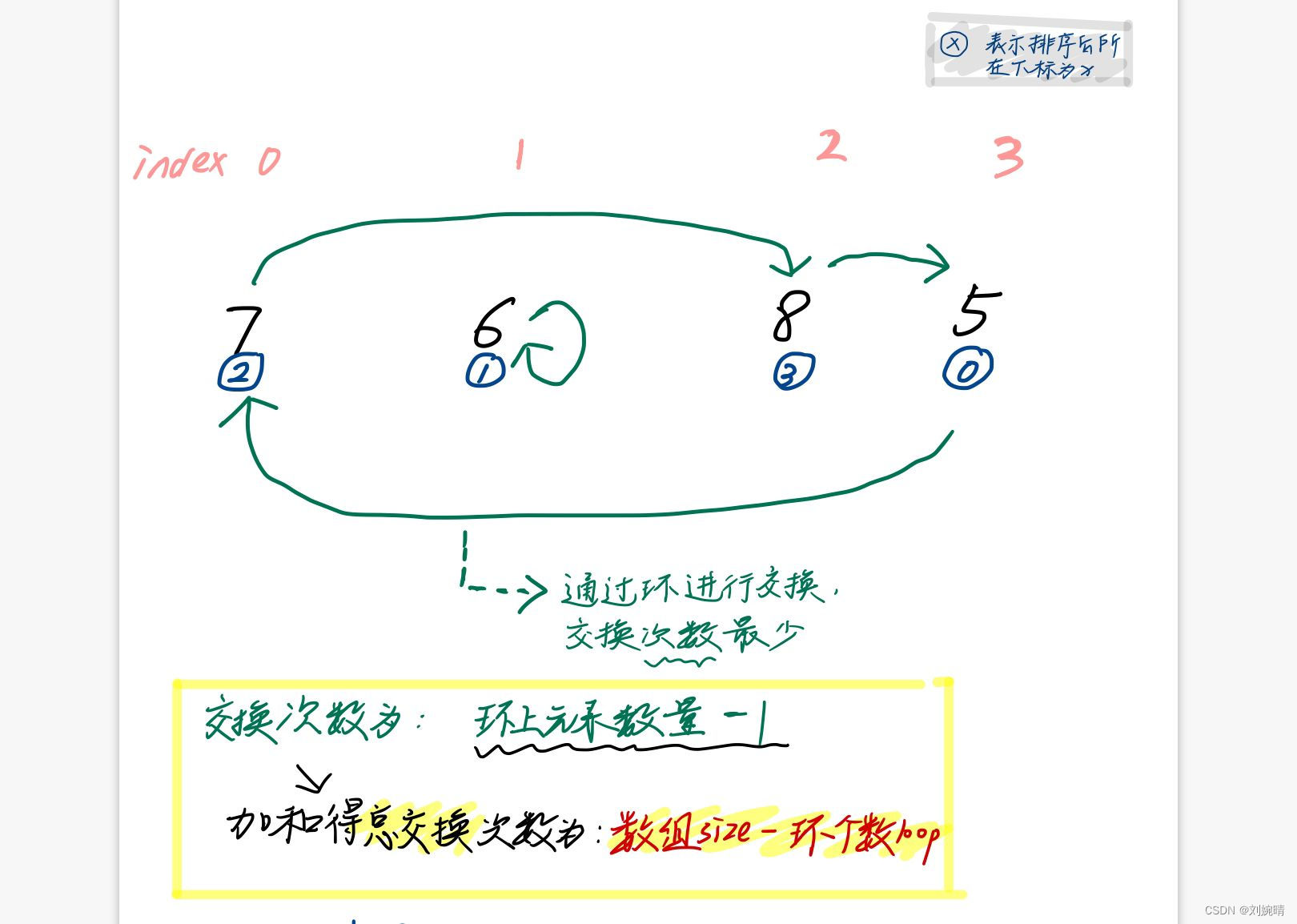
置换环算法一般情况代码如下：

    // 返回使得 nums 递增需要的最小交换元素次数
    public int minChanges(int[] nums){
        int[] copy = Arrays.copyOf(nums, nums.length);
        Arrays.sort(copy);
        HashMap<Integer, Integer> map = new HashMap<>();
        for(int i=0; i<copy.length; i++){
            map.put(copy[i], i);
        }
        boolean[] flag = new boolean[nums.length];  // 用于标记 nums[i] 是否已经被加入环中
        int loop = 0; // 环的个数
        for(int i=0; i<nums.length; i++){
            if(!flag[i]){
                int j = i;
                while(!flag[j]){ // 画环
                    int index = map.get(nums[j]); // 当前节点指向的位置，画环过程
                    flag[j] = true; // 将 j 加入环中
                    j = index; // 将当前节点移动到环上下个节点
                }
                loop++; // 环数递增
            }
        }
        return nums.length - loop; // 最小交换次数为 ： 数组长度 - 环数
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

三、代码

综合上述思路，得到本题代码如下：

    // 逐层排序二叉树
    public int minimumOperations(TreeNode root) {

        int res = 0;
        // 树为 null 的情况
        if(root == null){
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            List<Integer> levelList = new ArrayList<>();
            int size  = queue.size();
            
            // 得到该层全部节点
            for(int i=0; i<size; i++){
                TreeNode node = queue.poll();
                levelList.add(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            
            int loop = 0;
            // 得到该层节点交换次数
            List<Integer> temp = new ArrayList<>(levelList);
            boolean[] flag = new boolean[temp.size()];
            Collections.sort(levelList);
            HashMap<Integer, Integer> map = new HashMap<>();
            for(int i=0; i<levelList.size(); i++){
                map.put(levelList.get(i), i);
            }
            for(int i=0; i<temp.size(); i++){
                if(!flag[i]){
                    int j = i;
                    while(!flag[j]){
                        int index = map.get(temp.get(j));
                        flag[j] = true;
                        j = index;
                    }
                    loop++;
                }
            }
            
            res += (temp.size() - loop);
        }
        return res;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

尾注： 在本题实现过程中，最开始我没有提前使用 map 建立排序后元素值和其下标关系的哈希表，而是使用 indexOf API 在每次循环时判断当前元素应该在的位置，这种方式在节点值非常多时，出现了超时问题，这也确实证明了使用 Hash表查找能够显著的提高查询效率，于此切记，不要犯懒，记得要用 HashMap