LeetCode-790. 多米诺和托米诺平铺【动态规划,矩阵快速幂】

题目描述：

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 “L” 的托米诺形。两种形状都可以旋转。

给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

示例 1:

输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。
示例 2:

输入: n = 1
输出: 1

提示：

1 <= n <= 1000

https://leetcode.cn/problems/domino-and-tromino-tiling/

解题思路一：动态规划。四种状态。

一个正方形都没有被覆盖，记为状态 0；

只有上方的正方形被覆盖，记为状态 1；

只有下方的正方形被覆盖，记为状态 2；

上下两个正方形都被覆盖，记为状态 3。

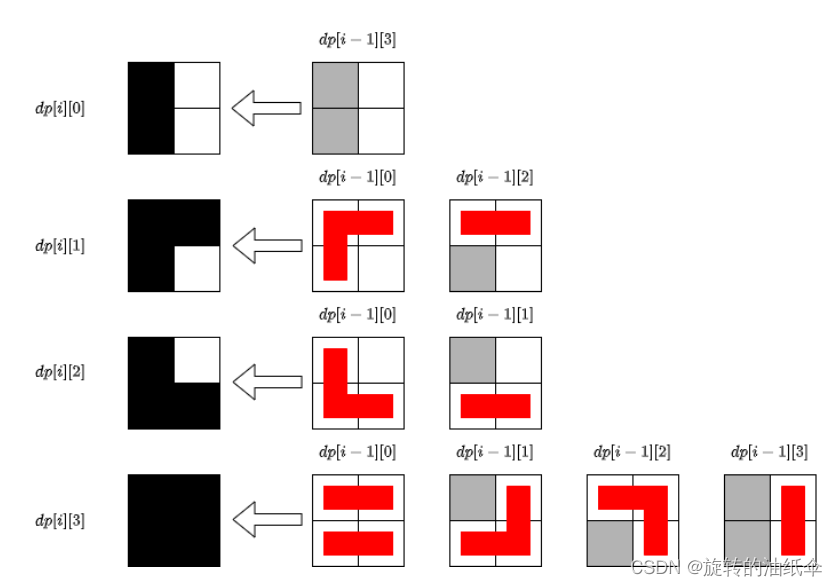
1.黑色正方形，前一列是i-1，后一列是i。2.红色条表示新铺的瓷砖。

难以理解的是：
初始时 dp[0][0]=0,dp[0][1]=0,dp[0][2]=0,dp[0][3]=1
我们从n=1开始。

最后平铺到第 n 列时，上下两个正方形都被覆盖的状态 dp[n][3]对应的平铺方法数量就是总平铺方法数量。

const long long mod = 1e9 + 7;
class Solution {
public:
    int numTilings(int n) {
        vector<vector<long long>> dp(n + 1, vector<long long>(4));
        dp[0][3] = 1;
        for (int i = 1; i <= n; i++) {
            dp[i][0] = dp[i - 1][3];
            dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % mod;
            dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
            dp[i][3] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][3]) % mod;
        }
        return dp[n][3];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

时间复杂度：O(n)
空间复杂度：O(n)

解题思路二：矩阵快速幂

n&1与n%2==1相同。

const long long mod = 1e9 + 7;
class Solution {
public:
    vector<vector<long long>> mulMatrix(const vector<vector<long long>> &m1, const vector<vector<long long>> &m2) {
        int n1 = m1.size(), n2 = m2.size(), n3 = m2[0].size();
        vector<vector<long long>> res(n1, vector<long long>(n3));
        for (int i = 0; i < n1; i++) {
            for (int k = 0; k < n3; k++) {
                for (int j = 0; j < n2; j++) {
                    res[i][k] = (res[i][k] + m1[i][j] * m2[j][k]) % mod;
                }
            }
        }
        return res;
    }

    int numTilings(int n) {
        vector<vector<long long>> mat = {
            {0, 0, 0, 1},
            {1, 0, 1, 0},
            {1, 1, 0, 0},
            {1, 1, 1, 1}
        };
        vector<vector<long long>> matn = {
            {1, 0, 0, 0},
            {0, 1, 0, 0},
            {0, 0, 1, 0},
            {0, 0, 0, 1}
        };
        while (n) {
            if (n & 1) {
                matn = mulMatrix(matn, mat);
            }
            mat = mulMatrix(mat, mat);
            n >>= 1;
        }
        return matn[3][3];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

时间复杂度：O(logn)
空间复杂度：O(1)

解题思路三：0

1