概率论之巴拿赫的火柴盒问题

1.巴拿赫的火柴盒问题

巴拿赫 Stefan Banach 是 20 世纪初最重要的数学家之一——如果你对流行数学感兴趣，你就会听说过 Banach-Tarski 悖论；如果你做过任何严肃的线性代数，你就会知道巴拿赫空间；如果你读过《破解数学》，你就会从苏格兰咖啡馆的章节中认出他的名字。 很明显，从以他命名的事物列表中选择了一个不太严肃的例子：巴拿赫的火柴盒问题。这个问题应该并不直接归咎于巴拿赫，这个概率问题主要是想取笑巴拿赫抽了多少烟，更确切地说是关于火柴盒与火柴的问题。

                                

问题描述

爱抽烟的数学家巴拿赫教授在左右口袋各放入了一盒火柴，他每次吸烟时，都随机的从左右口袋中掏出一盒火柴点烟（从左右口袋掏火柴盒的概率均为1/2），而且每次掏火柴的习惯是相互独立的。假定开始时左右口袋中的火柴盒各放入火柴根数为n。在每一天，他从任一口袋中随机取出一根火柴。在某个时候，他伸手去拿一根火柴，发现他挑选的盒子是空的，那么另一个口袋中的火柴盒中的火柴根数的分布列是什么？如果从左口袋掏火柴盒的概率是p，从右口袋掏火柴盒的概率为 1-p, 相应的结果又会是什么？

设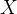是一个火柴盒为空，另一个火柴盒中火柴的根数.对于,定义（或）分别为这样的随机事件：当第一次发现一个火柴盒为空火柴盒的时候，这个火柴盒是左或者右口袋里的火柴盒，并且右（或者左）火柴盒里剩下 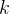 根火柴。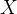 的分布列为：

                                                

进一步地，我们定义选择左口袋为一次成功，选择右口袋为一次失败事件。则是这样的事件：前次事件中成功了 次，在次试验的时候也是成功，这样对于 

                

利用对称性 ，可知对于 ，得到

                        

对问题推广后，即从左口袋取火柴的概率为,右口袋取火柴的概率为,利用相似性推理得到：

                        P(Lk)=p(n−k+nn)⋅pn(1−p)n−k,k=0,1,...,nP(Lk)=p(n−k+nn)⋅pn(1−p)n−k,k=0,1,...,n

        ​​​​​​​        ​​​​​​​        P(Rk)=(1−p)(n−k+nn)⋅pn−k(1−p)n,k=0,1,...,nP(Rk)=(1−p)(n−k+nn)⋅pn−k(1−p)n,k=0,1,...,n

由此得到

           pX(k)=P(Lk)+P(Rk)=(2n−kn)⋅(pn+1(1−p)n−k+pn−k(1−p)n+1)

2.赌徒破产问题

3.赌本分割问题

泰里思和温迪在玩18个洞的高尔夫球，其奖金为10元钱。他们各自赢得一 个洞的概率分别为p（泰里思）和(1−p)（温迪），并且各个洞的输赢是相互独立的。打完10个洞的时候，他们的比分为4:6，温迪占上风。此时泰里思接到一个紧急电话，必须回单位工作。他们决定按照他们打完比赛时候赢得比赛的概率分割奖金。假定pT(pW)代表在目前10个洞的比分4:6的条件下，完成18个洞的比赛后泰里思（温迪）领先的概率，则泰里思应得10pTpT+pw​​​​​​​元，而温迪应得10pWpT+pW元。泰里思应该分得多少钱？

这是著名的点数问题一个例子，也就是赌本分割问题，对此类问题，帕斯卡提出的想法是：赌本分割问题应当按中断的条件下双方各自赢得赌博的条件概率进行分配。我们来推理下。
　　由题意可得：

                        p_T=P(泰里思在剩余的八个洞中至少打进6个洞) 
                        p_W=P(温迪在剩余的八个洞中至少打进4个洞)

运用一下二项分布的公式可得

        ​​​​​​​        ​​​​​​​        ​​​​​​​        pT=Σ8k=6(8k)pk(1−p)8−k

        ​​​​​​​        ​​​​​​​        ​​​​​​​        pW=Σ8k=4(8k)pk(1−p)8−k

　因此可以计算出泰里思应得的钱数。

4.两个信封之谜

你收到两个信封，每个信封内有若干钞票，钞票的数目都是整数（以元为单位），但两个信封内的钱数是不相同的。两个信封内的钱数可以认为是未知的常数。当你随机地打开一个信封以后，这个信封中的钱就是你的了，为了多拿钱。你还可以改变主意，决定拿另一个信封中的钱。一个朋友声称有一个策略，可以使拿到钱数较大的信封的概率超过1/2。其方法如下：你连续地抛掷一枚硬币，直到出现正面出现为止，令x为你抛掷硬币的次数再加上1/2。如果你头一次打开的信封里的钱数少于x，你就换信封，否则不换，你的朋友的方法可行吗？

初刚看到这个问题时，感觉这两件事完全没有关联啊，然后看了推理之后，才觉得真的是太机智了。我们记ˉm和m_分别是信封中较大的钱数和较小的钱数，那么关于x总共会有三种事件发生：

        ​​​​​​​        A={X<m_},B={m_<X<¯m},C={¯m<X}

¯A,¯B,¯C是满足对应的事件A,B,C发生，并且你第一次挑选的信封中包含¯m的事件，同理A_,B_,C_,是包含 m_ 的事件。
考虑如下事件：

                W = {挑选结束时你的信封中包含¯m}

由条件概率得：

                ​​​​​​​        P(W|A)amp;=12(P(W|¯A)+P(W|A_))=12(1+0)=12P(W|B)amp;=12(P(W|¯B)+P(W|B_))=12(1+1)=1P(W|C)amp;=12(P(W|¯C)+P(W|C_))=12(0+1)=12

由全概率公式计算P(W)，得：

        ​​​​​​​                P(W)amp;=P(A)P(W|A)+P(B)P(W|B)+P(C)P(W|C)amp;=12(P(A)+P(B)+P(C))+12P(B)amp;>12

所以这个策略是对的。

5.拉普拉斯继承性准则

设有m+1个盒子，第k 个盒子里有 k个红球，m−k个白球，0≤k≤m

随便选取一个盒子，独立有放回抽一个球，抽  n次。假设n 次都是红球，那再抽一个球为红球的概率是多少?m很大时这个概率会如何？

解：记E为第n+1 次为红球的事件，Rn为n次抽取都是红球的时间。由于连续抽取红球，所以盒子里面应该会有很多红球，于是P(E|Rn)≈1.

事实上，拉普拉斯利用此例去计算给定5000年中每天日出的条件下明天日出的概率。

根据贝叶斯公式：

                                                P(E|Rn)=P(E∩Rn)P(Rn)

再由全概率公式得：

        ​​​​​​​                P(Rn)=Σmk=0P(chooseKth)(km)n=1m+1Σmk=0(km)n

        ​​​​​​​                P(E∩Rn)=P(Rn+1)=1m+1Σmk=0(km)n+1

如果m很大，可将求和项看成积分的近似值

        P(Rn)=1m+1Σmk=0(km)n≈1(m+1)mn∫m0xndx=1(m+1)mnmn+1n+1

  也就是：

                                                      P(Rn)=m(m+1)(n+1)≈1n+1​​​​​​​

同理
                                        P(E∩Rn)=P(Rn+1)≈1n+2

从而，

                                                P(E|Rn)≈n+1n+2

当m和很大时，抽取红球几乎是必然的.