• 【动手学深度学习PyTorch版】2 线性回归

    参考视频按特定轴求和_哔哩哔哩_bilibili

    目录

    一、自动求导

    ◼ 相关知识

    # 计算图

    # 反向累积

    ◼ 自动求导代码实现

    二、线性回归

    ◼ 举例：房价预测

    # 线性回归模型

    # 训练数据

    # 参数学习

    # 显示解（最优解）

    # 线性回归总结

    三、单元线性回归实现：糖尿病例子

    ◼ 生成数据集

    # np.newaxis

    # 比较两个数组是否等同

    # 随机采样

    # 将数组打乱随机排列

    ◼ 训练集与测试集的划分

    ◼ 训练数据

    四、线性回归从0开始实现（使用自定义）

    4.1 生成数据集

    4.2 绘制数据集

    4.3 读取小批量

    4.4 训练模型 

    4.5 完整代码

     五、线性回归（使用框架）

    一、自动求导

    ◼ 相关知识

     

     

     自动求导：计算一个函数在指定值上的导数，它有别于：

    • 符号求导：求具体的函数的导；
    • 数值求导：我不需要知道f(x)具体是什么，用数值去拟合；

    # 计算图

    计算图：其中节点对应于数学运算。 计算图是表达和评估数学表达式的一种方式。

     

    # 反向累积

     

    深度学习耗很多存储，就是因为反向累积这部分需要存储很多中间结果。

    ◼ 自动求导代码实现

    ① 假设想对函数，关于列向量x求导。

    ② 在外面计算y关于x的梯度之前，需要一个地方来存储梯度。

    ③ 现在计算y。

    ④ 通过调用反向传播函数来自动计算y关于x每个分量的梯度。

    其中的“grad_fn=”指的是：y是从x计算过来的。

     ⑤ 计算x的另一个函数。

     ⑥ 在深度学习中，目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和。

    其中，y.sum().backward()：我们一般会对y进行求和y.sum()后，就将向量y转为标量了，对标量求导。

     ⑦ 将某些计算移动到记录的计算图之外。

    ⑧ 即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），仍然可以计算得到的变量的梯度。 

     

    二、线性回归

    ◼ 举例：房价预测

    # 线性回归模型

     把它拓展到线性模型，

    线性模型可以看做是单层神经网络。

    # 训练数据

    # 参数学习

    # 显示解（最优解）

    # 线性回归总结

    三、单元线性回归实现：糖尿病例子

    ◼ 生成数据集

    1. import pandas as pd
    2. import numpy as np
    3. import matplotlib.pyplot as plt
    4. from sklearn import datasets, linear_model
    5. from sklearn.metrics import mean_squared_error, r2_score
    6.  
    7. # 1.导入数据集
    8. diabetes = datasets.load_diabetes()
    9. diabetes

    我们可以大致看一下这个数据集：422个样本，10个特征。

    1. print(diabetes.data)    # x
    2. print(diabetes.data.shape)    # 422个样本，10个特征
    3. print(diabetes.target)     # y

    # np.newaxis

    np.newaxis：np.newaxis 在使用和功能上等价于 None，可以给原数组增加一个维度； np.newaxis放的位置不同，产生的新数组也不同。

    如果我们单取二维数组的某一列的话，就会导致出来的是一维的数组，在切片的时候使用np.newaxis就可以让我们取出来的数组还是二维数组(442, 1)。

    其实，这个np.newaxis方法的功能与.reshape类似，我们要看.reshape(-1,1)里的1所对应的位置为列，-1就代表我不知道它有多少行。无论多少行，我只要保证列数是1列。得到的也是二维数组(442, 1)。

    # 比较两个数组是否等同

    np.array_equal(d1,d2)： 比较两个array在shape与所含的值是否相同，等同于(d1==d2).all()；

     (d1==d2).all()：其中.all()的作用是只要数组中有一个False，就说明两个array所含的值不相同；

    # 随机采样

    DataFrame.sample() ：直接打乱样本

    DataFrame.sample(n=None, frac=None, replace=False, random_state=None, axis=None)

    • n:整数，表示你要随机抽取几行数据，比如你要抽取10行，n=10。不能与frac同时使用。
    • frac:浮点型，可选。相对比例，表示抽取数据的百分比。不能与n同时使用。
    • replace：布尔值，可选。原来的DataFrame是否被抽取的数据替换，默认为False。
    • random_state：随机种子数
    • axis： 整数型或字符串，默认axis=0从行中抽取。axis=0从行中抽取数据，axis=1从列中抽取数据。

     

    DataFrame转化回array：

    • np.array(pd.DataFrame(diabetes_X).sample(10, random_state=1))
    • pd.DataFrame(diabetes_X).sample(10, random_state=1).values

    # 将数组打乱随机排列

    两种方法：

    • np.random.shuffle(x)：在原数组上进行，改变自身序列，无返回值。
    • np.random.permutation(x)：不在原数组上进行，返回新的数组，不改变自身数组。

     

    ◼ 训练集与测试集的划分

    后20行数据作为测试集，后20行以外的数据都作为训练集。

    ◼ 训练数据

    mean_squared_error(diabetes_y_test, diabetes_y_pred))，均方误差，（真实值-预测值）之差->平方->求和->平均。即线性回归的损失函数，这个损失函数越小越好。

    r2_score(diabetes_y_test, diabetes_y_pred)，即R方，反映模型拟合优度的统计量。R方取值在0到1之间，其值反映了因变量y的总方差中回归模型所能解释那部分的百分比。

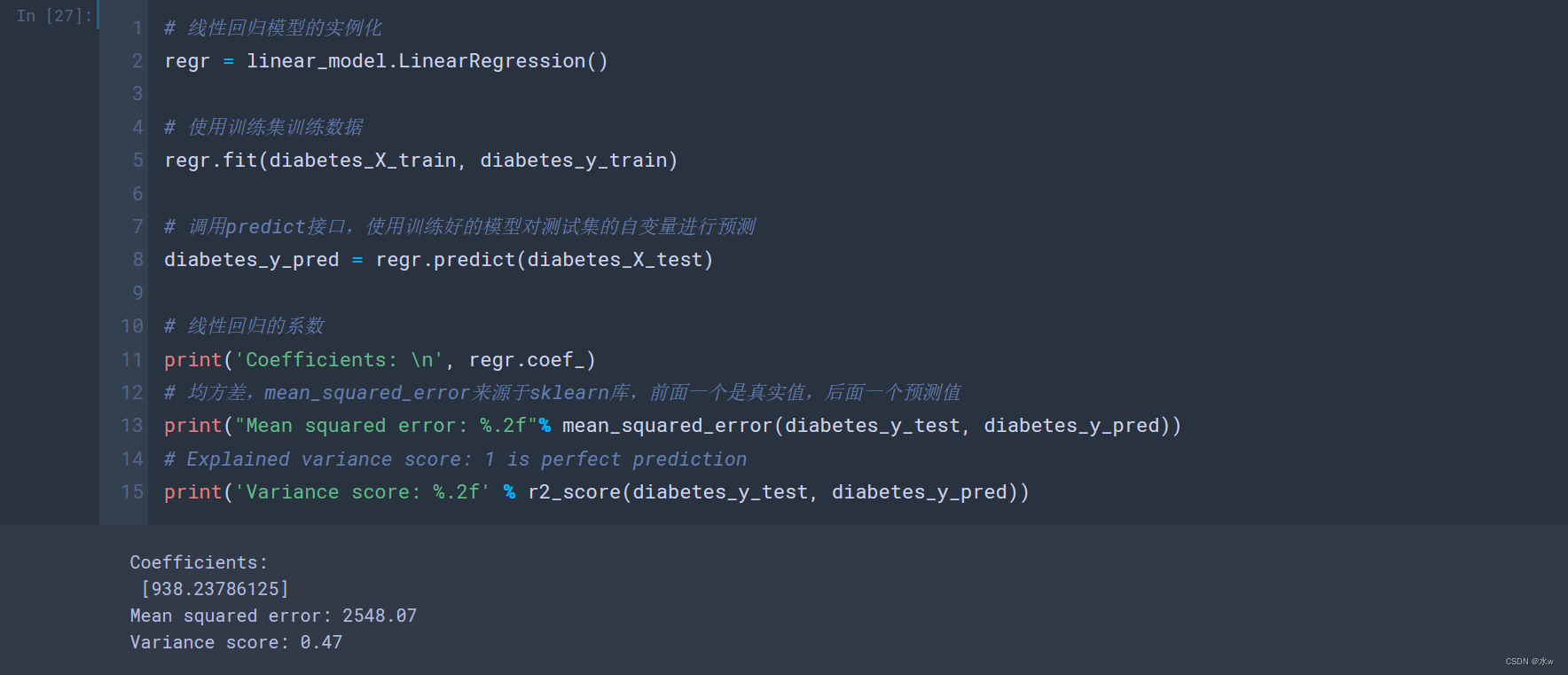
     得到的均方误差为2548.07，

    可视化 ：

     

    四、线性回归从0开始实现（使用自定义）

    将从零开始实现整个方法，包括数据流水线、模型、损失函数和小批量随即梯度下降优化器。

    4.1 生成数据集

    ① 根据带有噪声的线性模型构造一个人造数据集。我们使用线性模型参数、和噪声项ϵ生成数据集及其标签：。

    4.2 绘制数据集

    ① features中每一行都包含一个二维数据样本，labels中的每一行都包含一维标签值（一个标签）。

    4.3 读取小批量

    4.4 训练模型 

    定义模型，损失函数，优化算法，

    训练过程：

    4.5 完整代码

    1. %matplotlib inline
    2. import random
    3. import torch
    4. from d2l import torch as d2l
    5.  
    6. def synthetic_data(w,b,num_exaples):
    7.     """生成 y = Xw + b + 噪声"""
    8.     X = torch.normal(0,1,(num_exaples,len(w)))
    9.     y = torch.matmul(X,w) + b
    10.     y += torch.normal(0,0.01,y.shape)
    11.     return X, y.reshape((-1,1))
    12.  
    13. true_w = torch.tensor([2,-3.4])
    14. true_b = 4.2
    15. features, labels = synthetic_data(true_w, true_b, 1000)
    16. print('features:',features[0],'\nlabel:',labels[0])
    17.  
    18. d2l.set_figsize()
    19. d2l.plt.scatter(features[:,(1)].detach().numpy(),labels.detach().numpy(),1)   
    20.  
    21. def data_iter(batch_size,features,labels):
    22.     num_examples = len(features)  # 样本个数
    23.     indices = list(range(num_examples)) # 样本索引
    24.     # 这些样本是随即读取的，没有特定的顺序
    25.     random.shuffle(indices) # 把索引随即打乱
    26.     for i in range(0, num_examples, batch_size):
    27.         batch_indices = torch.tensor(indices[i:min(i+batch_size,num_examples)]) # 当i+batch_size超出时，取num_examples         
    28.         yield features[batch_indices], labels[batch_indices] # 获得随即顺序的特征，及对应的标签
    29.         
    30. batch_size = 10
    31. for X,y in data_iter(batch_size, features, labels):
    32.     print(X, '\n', y) # 取一个批次后，就break跳出了
    33.     break
    34.  
    35. # 定义初始化模型参数
    36. w = torch.normal(0,0.01,size=(2,1),requires_grad=True)
    37. b = torch.zeros(1,requires_grad=True)
    38.  
    39. # 定义模型
    40. def linreg(X,w,b):
    41.     """线性回归模型"""
    42.     return torch.matmul(X,w)+b
    43.  
    44. # 定义损失函数
    45. def squared_loss(y_hat,y):
    46.     """均方损失"""
    47.     return (y_hat - y.reshape(y_hat.shape))**2/2 # 将y统一成与y_hat一样同尺寸   
    48.  
    49. # 定义优化算法
    50. def sgd(params,lr,batch_size):
    51.     """小批量随即梯度下降"""
    52.     with torch.no_grad(): # 不要产生梯度计算，减少内存消耗
    53.         for param in params: # 每个参数进行遍历
    54.             param -= lr * param.grad / batch_size # 每个参数进行更新，损失函数没有求均值，所以这里除以 batch_size 求了均值。由于乘法的线性关系，这里除以放在loss的除以是等价的。                          
    55.             param.grad.zero_() # 每个参数的梯度清零
    56.  
    57. # 训练过程
    58. lr = 0.03
    59. num_epochs = 3
    60. net = linreg # 这里用线性模型，这样写是很方便net赋予其他模型，只需要改一处，不需要下面所有网络模型名称都改
    61. loss = squared_loss
    62.  
    63. # 训练过程
    64. for epoch in range(num_epochs):
    65.     for X,y in data_iter(batch_size,features,labels):
    66.         l = loss(net(X,w,b),y) # x和y的小批量损失
    67.         # 因为l是形状是(batch_size,1)，而不是一个标量。l中所有元素被加到一起
    68.         # 并以此计算关于[w,b]的梯度
    69.         l.sum().backward()
    70.         sgd([w,b],lr,batch_size) #使用参数的梯度更新参数
    71.     with torch.no_grad():
    72.         train_l = loss(net(features,w,b),labels)
    73.         print(f'epoch{epoch+1},loss{float(train_l.mean()):f}')   
    74.  
    75. # 比较真实参数和通过训练学到的参数来评估训练的成功程度
    76. print(f'w的估计误差：{true_w-w.reshape(true_w.shape)}')
    77. print(f'b的估计误差：{true_b-b}')

     五、线性回归（使用框架）

    1. import numpy as np
    2. import torch
    3. from torch.utils import data
    4. from d2l import torch as d2l
    5. from torch import nn    
    6.     
    7. true_w = torch.tensor([2,-3.4])
    8. true_b = 4.2
    9. features, labels = d2l.synthetic_data(true_w,true_b,1000) # 库函数生成人工数据集    
    10.  
    11. # 调用框架现有的API来读取数据
    12. def load_array(data_arrays,batch_size,is_train=True):
    13.     """构造一个Pytorch数据迭代器"""
    14.     dataset = data.TensorDataset(*data_arrays) # dataset相当于Pytorch的Dataset。一个星号*，表示对list解开入参。      
    15.     return data.DataLoader(dataset,batch_size,shuffle=is_train) # 返回的是从dataset中随机挑选出batch_size个样本出来     
    16.  
    17. batch_size = 10
    18. data_iter = load_array((features,labels),batch_size) # 返回的数据的迭代器
    19. print(next(iter(data_iter))) # iter(data_iter) 是一个迭代器对象，next是取迭代器里面的元素  
    20.  
    21. # 使用框架的预定义好的层
    22. # nn是神经网络的缩写
    23. net = nn.Sequential(nn.Linear(2,1))
    24.  
    25. # 初始化模型参数
    26. net[0].weight.data.normal_(0,0.01) # 使用正态分布替换掉weight变量里面的数据值
    27. net[0].bias.data.fill_(0)  # 偏差bias变量里面的值设置为0
    28. print(net[0])
    29.  
    30. # 计算均方误差使用的是MSELoss类，也称为平方L2范数
    31. loss = nn.MSELoss()  #L1是算术差，L2是平方差
    32.  
    33. # 实例化SGD实例
    34. trainer = torch.optim.SGD(net.parameters(),lr=0.03)
    35.  
    36. # 训练过程代码与从零开始时所做的非常相似
    37. num_epochs = 3
    38. for epoch in range(num_epochs):
    39.     for X, y in data_iter:  # 从DataLoader里面一次一次把所有数据拿出来
    40. #         print("X:",X)
    41. #         print("y:",y)
    42.         l = loss(net(X),y) # net(X) 为计算出来的线性回归的预测值
    43.         trainer.zero_grad() # 梯度清零
    44.         l.backward()
    45.         trainer.step()  # SGD优化器优化模型
    46.     l = loss(net(features),labels)
    47.     print(f'epoch{epoch+1},loss{l:f}')

  • 相关阅读:
    kaggle大模型竞赛优胜方案总结与思考
    Android Studio 实现登录注册-源代码 （连接MySql数据库）
    如何理解Linux下的文件描述符 ？以及Linux下的重定向与缓冲区这一概念？？？
    linux5-make、库文件（静态库和共享库）
    SRS5.0-报错： srt serve error code=6006
    使用MapStruct简化entity、dto、dxo之间的属性复制
    springboot身体健康问诊信息系统毕业设计源码181049
    Python之字符串判断
    linux环境下tomcat中catalina.out文件过大问题
    AP5186 三功能内部VDD稳压管过温保掮 LED驱动IC
  • 原文地址：https://blog.csdn.net/qq_45956730/article/details/127296616