Matlab之四阶龙格—库塔法方法：解常微分初值问题

目录

1. 题目

2. 算法原理

3. 代码

4. 结果

4.1 运行结果

4.2 结果分析

---

【若觉文章质量良好且有用，请别忘了点赞收藏加关注，这将是我继续分享的动力，万分感谢！】

直接通过解题的方式进行学习，代入感更强

1. 题目

用经典四阶龙格库塔方法对初值问题{y′=−20yy(0)=1{y′=−20yy(0)=1，步长分别取求解，观察稳定区间的作用。

2. 算法原理

某些常微分方程有解析解，但大多数都没有，因此需要进行数值解计算。

龙格—库塔法是利用f(x,y)在某些特殊点上的函数值的线性组合，来估算高阶单步法的平均斜率。

经典的龙格—库塔法是四阶的，也就是在(xi,xi+1)(xi,xi+1)中用四个点处的斜率来估计其平局斜率，构成四阶龙格—库塔公式

其准确解y(x)在一系列点xi处y（xi）的近似值yi的方法，yi称为数值解。经典的四阶龙格库塔法方程如下：

yi+1=yi+c1K1+c2K2+c3K3+c4K4yi+1=yi+c1K1+c2K2+c3K3+c4K4

其中：

{K1=hf(xi,yi)K2=hf(xi+a2h,yi+b21K1)K3=hf(xi+a3h,yi+b31K1+b32K2)K4=hf(xi+a4h,yi+b41K1+b42K2+b43K3)

其中的各个参数具体如下：

a2=a3=b21=b32=12b31=b41=b42=0a4=b43=1c1=c4=16c2=c3=13

其整合之后为：

{yi+1=yi+16(K1+2K2+2K3+K4)K1=hf(xi,yi)K2=hf(xi+h2,yi+12K1)K3=hf(xi+h2,yi+12K2)K4=hf(xi+h,yi+K3)

其中h为步长。

3. 代码

clear;
clc;
 
for step = [0.1, 0.2]
    
    x_0 = 0;
    y_0 = 1;
    num = floor(1/step);
    n = 1;
    X_output = [0];
    Y_output = [1];
 
    disp("y'= -20 * y")
    while n <= num
        x_1 = x_0 + step;
        K_1 = step * fun(x_0,y_0);
        K_2 = step * fun(x_0 + step/2, y_0 + K_1/2);
        K_3 = step * fun(x_0 + step/2, y_0 + K_2/2);
        K_4 = step * fun(x_0 + step, y_0 + K_3);
        y_1 = y_0 + (K_1 + 2 * K_2 + 2 * K_3 + K_4) / 6 ;
        X_output = [X_output x_1];
        Y_output = [Y_output y_1];
        x_0 = x_1;
        y_0 = y_1;
        n = n + 1;
    end
    figure()
    plot(X_output,Y_output)
    xlabel('x')
    ylabel('y')
    title(['Runge-Kutta4阶,步长为：', num2str(step)])
    X_output
    Y_output
    clear X_output Y_output
end
 
[x,y] = ode45('fun', [0:1], 1);
figure()
plot(x,y)
xlabel('x')
ylabel('y')
title('自带函数求解结果')
 
function dy = fun(x, y)
dy = - 20*y;
end

4. 结果

4.1 运行结果

Step = 0.1 时
 
X_output =
0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000          
1.0000
 
Y_output =
1.0000    0.3333    0.1111    0.0370    0.0123    0.0041    0.0014    0.0005    0.0002    0.0001    0.0000
 
Step = 0.2时
X_output =
0    0.2000    0.4000    0.6000    0.8000    1.0000
 
Y_output =
1           5          25         125         625        3125

 

 

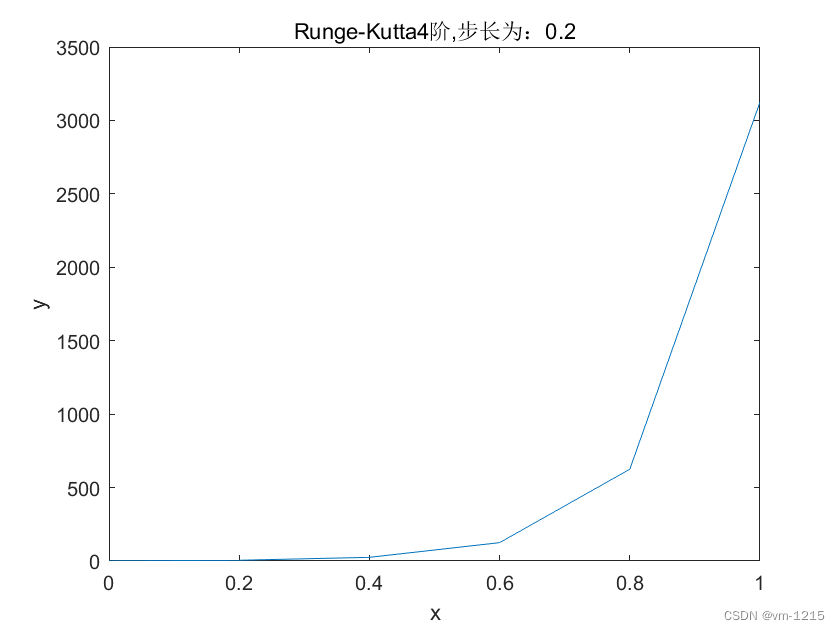
4.2 结果分析

用经典四阶龙格库塔方法求解,其求解结果与设置得步长有很大的相关性，步长设置合适时，其求解情况与真实值基本一致，趋于稳定。但步长加大时，其求解值与真实值相差太大。

​​​​​​​【若觉文章质量良好且有用，请别忘了点赞收藏加关注，这将是我继续分享的动力，万分感谢！】