-
高等工程数学 —— 第五章 (4)罚函数法
高等工程数学 —— 第五章 (4)罚函数法

外点罚函数法


做题时就是构造一个 σ P \sigma P σP然后计算两种情况的一阶必要条件未知量的值,若符合不等式约束就对其进行二阶必要条件验证。若成立就对 σ \sigma σ取无穷大然后得到最优解。
例:


- 这里求解 x ( σ ) x(\sigma) x(σ)时对于 x 1 + x 2 ≤ 4 x_1+x_2 \leq 4 x1+x2≤4这种情况解得 x 1 = 3 x_1 = 3 x1=3, x 2 = 2 x_2 = 2 x2=2。此时发现不满足 x 1 + x 2 ≤ 4 x_1+x_2 \leq 4 x1+x2≤4条件。
- 因此我们对于 x 1 + x 2 ≥ 4 x_1+x_2 \geq 4 x1+x2≥4这种情况求解。

- 对其进行二阶充分条件的验证

- 对 σ \sigma σ取无穷大可得可行点与最优值。
内点罚函数法
只适用于只有不等式约束的非线性最优化问题。



选取障碍函数构建罚函数,然后用一阶必要条件来求解可行点的值,再用二阶充分条件来验证。最后我们对 μ \mu μ趋近于0来得到最后的结果。
例1:

- 此处我们可以解出 x 1 = μ + 1 , x 2 = μ x_1 = \sqrt{\mu+1} , x_2 = \mu x1=μ+1,x2=μ

- 用二阶充分条件验证后将 μ \mu μ取0求解。
例2:

例3:

广义乘子法
这个好像用的比较少一点,但是老师说不排除不考,简单应用还是要会的。
等式约束问题
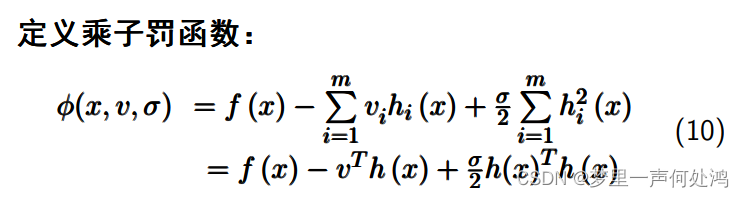

记住上述两个公式会做题就行了。例:




这里得到 v ( k ) v^{(k)} v(k)的步骤如下:
- 有一个简单的方法,我们可以令 v ( k + 1 ) = v ( k ) v^{(k+1)} = v^{(k)} v(k+1)=v(k)来求解这个递增的上界。即 v ( k ) = 1 6 v ( k ) + 1 3 v^{(k)} = \frac 16v^{(k)} + \frac 13 v(k)=61v(k)+31
不等式约束问题

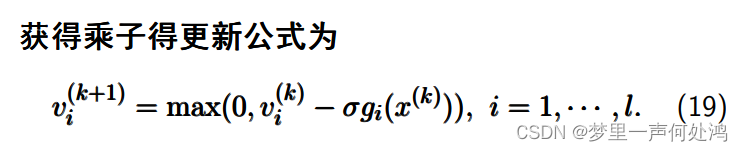 看例题吧,希望不考:
看例题吧,希望不考:

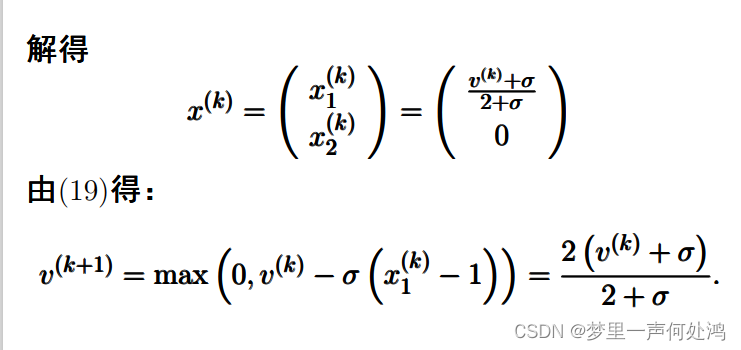

- 这里 v ( k ) → 2 v^{(k)} \to 2 v(k)→2也是令 v ( k + 1 ) = v ( k ) v^{(k+1)} = v^{(k)} v(k+1)=v(k)后求解 v ( k ) = 2 ( v ( k ) + σ ) 2 + σ v^{(k)} = \frac{2(v^{(k)}+\sigma)}{2+\sigma} v(k)=2+σ2(v(k)+σ)得到的。
例:

-
相关阅读:
opencascade 布尔运算笔记
各GIS软件添加天地图方式
认识电磁干扰?|深圳比创达EMC
C++编程题目------平面上的最接近点对(分治算法)
K8S:Pod
Tensorflow 2.x入门教程
Service
项目部署Linux步骤
【Android应用与开发】DAY1-安装Android Studio报错整合及学习
SCRUM产品负责人(CSPO)认证培训课程
- 原文地址:https://blog.csdn.net/Deam_swan_goose/article/details/127744909