JAVA线程池 -clt设计与分析

1. 前言

1. ctl 是线程池源码中常常用到的一个变量。
2. 它的主要作用是记录线程池的生命周期状态和当前工作的线程数。
3. 作者通过巧妙的设计，将一个整型变量按二进制位分成两部分，分别表示两个信息。

2. 源码解析

源码部分

    /**
     * The main pool control state, ctl, is an atomic integer packing
     * two conceptual fields
     *   workerCount, indicating the effective number of threads
     *   runState,    indicating whether running, shutting down etc
     *
     * In order to pack them into one int, we limit workerCount to
     * (2^29)-1 (about 500 million) threads rather than (2^31)-1 (2
     * billion) otherwise representable. If this is ever an issue in
     * the future, the variable can be changed to be an AtomicLong,
     * and the shift/mask constants below adjusted. But until the need
     * arises, this code is a bit faster and simpler using an int.
     *
     * The workerCount is the number of workers that have been
     * permitted to start and not permitted to stop.  The value may be
     * transiently different from the actual number of live threads,
     * for example when a ThreadFactory fails to create a thread when
     * asked, and when exiting threads are still performing
     * bookkeeping before terminating. The user-visible pool size is
     * reported as the current size of the workers set.
     *
     * The runState provides the main lifecycle control, taking on values:
     *
     *   RUNNING:  Accept new tasks and process queued tasks
     *   SHUTDOWN: Don't accept new tasks, but process queued tasks
     *   STOP:     Don't accept new tasks, don't process queued tasks,
     *             and interrupt in-progress tasks
     *   TIDYING:  All tasks have terminated, workerCount is zero,
     *             the thread transitioning to state TIDYING
     *             will run the terminated() hook method
     *   TERMINATED: terminated() has completed
     *
     * The numerical order among these values matters, to allow
     * ordered comparisons. The runState monotonically increases over
     * time, but need not hit each state. The transitions are:
     *
     * RUNNING -> SHUTDOWN
     *    On invocation of shutdown(), perhaps implicitly in finalize()
     * (RUNNING or SHUTDOWN) -> STOP
     *    On invocation of shutdownNow()
     * SHUTDOWN -> TIDYING
     *    When both queue and pool are empty
     * STOP -> TIDYING
     *    When pool is empty
     * TIDYING -> TERMINATED
     *    When the terminated() hook method has completed
     *
     * Threads waiting in awaitTermination() will return when the
     * state reaches TERMINATED.
     *
     * Detecting the transition from SHUTDOWN to TIDYING is less
     * straightforward than you'd like because the queue may become
     * empty after non-empty and vice versa during SHUTDOWN state, but
     * we can only terminate if, after seeing that it is empty, we see
     * that workerCount is 0 (which sometimes entails a recheck -- see
     * below).
     */
    private final AtomicInteger ctl = new AtomicInteger(ctlOf(RUNNING, 0));
    private static final int COUNT_BITS = Integer.SIZE - 3;
    private static final int CAPACITY   = (1 << COUNT_BITS) - 1;

    // runState is stored in the high-order bits
    private static final int RUNNING    = -1 << COUNT_BITS;
    private static final int SHUTDOWN   =  0 << COUNT_BITS;
    private static final int STOP       =  1 << COUNT_BITS;
    private static final int TIDYING    =  2 << COUNT_BITS;
    private static final int TERMINATED =  3 << COUNT_BITS;

    // Packing and unpacking ctl
    private static int runStateOf(int c)     { return c & ~CAPACITY; }
    private static int workerCountOf(int c)  { return c & CAPACITY; }
    private static int ctlOf(int rs, int wc) { return rs | wc; }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

基础常量

线程池运行的状态，并不是用户显式设置的，而是伴随着线程池的运行，由内部来维护。
线程池内部使用一个原子整型变量 ctl 维护两个值：运行状态(runState)和线程数量 (workerCount) 其中高3位保存runState，低29位保存workerCount当前池线程数。如下代码所示：

  // 初始化ctl值为0，并设置状态为RUNNING
  private final AtomicInteger ctl = new AtomicInteger(ctlOf(RUNNING, 0));
  // 结果：32-3=29,就用来表示分隔runState 和workerCount 的位数
  // 之所以-3，因为线程池的生命周期有 5 个状态，为了表达这 5 个状态，我们需要 3 个二进制位。
  private static final int COUNT_BITS = Integer.SIZE - 3;
  // 结果：000 1   1111 1111 1111 1111 1111 1111 1111
  private static final int CAPACITY   = (1 << COUNT_BITS) - 1;
1
2
3
4
5
6
7

目前我们已经有了三个变量信息（如何使用这三个值，请看下文）：

• clt:保存了运行状态(runState)和线程数量 (workerCount) 的值
• COUNT_BITS：29，分隔runState 和workerCount 的位数
• CAPACITY（2进制）：000 1 1111 1111 1111 1111 1111 1111 1111,前三位为0，后29位为1

可能你对【CAPACITY】二进制的值有所疑惑，那么我们来看看推演过程

1. (1 << COUNT_BITS) - 1可平替为  (1 << 29) - 1
2. 首先看 1 的二进制代表 	0000 0000 0000 0000 0000 0000 0000 0001。
3. 向左移 29 位得到 		0010 0000 0000 0000 0000 0000 0000 0000。
4. 数据减 1 得到 			0001 1111 1111 1111 1111 1111 1111 1111。

1
2
3
4
5

---

我们都知道线程池有五个状态，它在线程池中分布是如下表示的：

• RUNNING：能接受新提交的任务，并且也能处理阻塞队列中的任务。
• SHUTDOWN：指调用了 shutdown() 方法，不再接受新提交的任务，但却可以继续处理阻塞队列中已保存的任务。
• STOP：指调用了 shutdownNow() 方法，不再接受新提交的任务，同时抛弃阻塞队列里的所有任务并中断所有正在执行任务。
• TIDYING： 所有任务都执行完毕，workerCount 有效线程数为 0。
• TERMINATED：终止状态，当执行 terminated() 后会更新为这个状态。

源码如下

	// 结果29
	private static final int COUNT_BITS = Integer.SIZE - 3;
	// runState is stored in the high-order bits
    private static final int RUNNING    = -1 << COUNT_BITS;
    private static final int SHUTDOWN   =  0 << COUNT_BITS;
    private static final int STOP       =  1 << COUNT_BITS;
    private static final int TIDYING    =  2 << COUNT_BITS;
    private static final int TERMINATED =  3 << COUNT_BITS;
1
2
3
4
5
6
7
8

我们来推算下他们值（2进制表示）

/**
 * 各个值的二进制表示：
 *
 * 1111 1111 1111 1111 1111 1111 1111 1111 (-1) 
 * 0000 0000 0000 0000 0000 0000 0000 0000 (0) 
 * 0000 0000 0000 0000 0000 0000 0000 0001 (1) 
 * 0000 0000 0000 0000 0000 0000 0000 0010 (2) 
 * 0000 0000 0000 0000 0000 0000 0000 0011 (3)
 *
 * 【分析】：
 * 初始容量值，高三位全是0，低29位全是1；后续操作会以此为基础进行操作
 * CAPACITY(29)                000 1   1111 1111 1111 1111 1111 1111 1111
 *
 *              ---------------3位-1位 -28位---
 * 【前三位，表明状态位，后29位表明线程个数，即 2^29 - 1 基本够用了】
 *
 * RUNNING(-536870912)         111 0    0000 0000 0000 0000 0000 0000 0000
 * SHUTDOWN(0)                 000 0    0000 0000 0000 0000 0000 0000 0000
 * STOP(536870912)             001 0    0000 0000 0000 0000 0000 0000 0000
 * TIDYING(1073741824)         010 0    0000 0000 0000 0000 0000 0000 0000
 * TERMINATED(1610612736)      011 0    0000 0000 0000 0000 0000 0000 0000
 * 
 * /
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

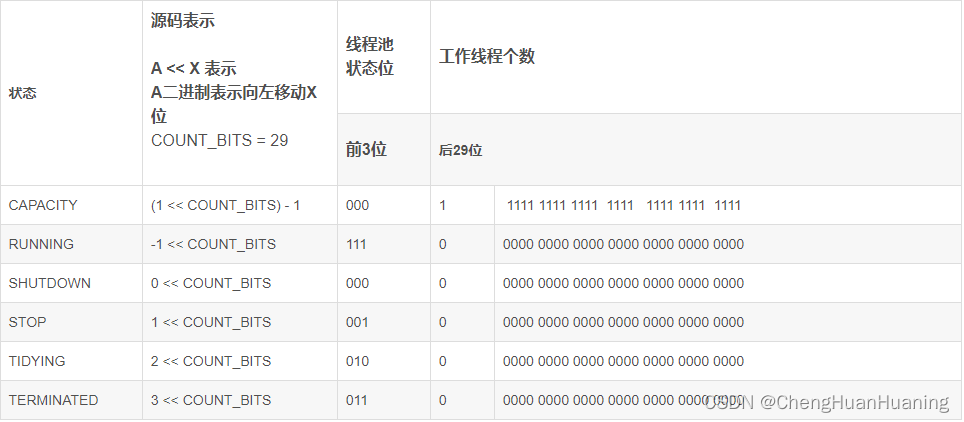
根据以上分析得,我们只需要重点关注高三位：

• RUNNING：对应的高3位值是111
• SHUTDOWN：对应的高3位值是000。
• STOP： 对应的高3位值是001。
• TIDYING：对应的高3位值是010。
• TERMINATED：对应的高3位值是011。

打包函数与拆包函数

拆包函数

上面我们曾说过，线程池内部使用一个原子整型变量 ctl 维护两个值：运行状态(runState)和线程数量 (workerCount) 其中高3位保存runState，低29位保存workerCount当前池线程数
这样我们就可以知道这两个方法的目的：获取当前参数的高3位和低29位

    // 获取当前运行状态
    private static int runStateOf(int c) { 
        return c & ~CAPACITY; 
    }
    // 获取工作线程数
    private static int workerCountOf(int c) { 
        return c & CAPACITY; 
    }
1
2
3
4
5
6
7
8

让我们复习下&（与运算）： 只要有0则为0
让我们复习下|（或运算）： 只要有1则为1

运行状态
c & ~CAPACITY ：意为CAPACITY取反后与c进行&操作，得到当前入参二进制的前三位（运行状态）

我们以c为【RUNNING】状态举例
CAPACITY结果			000  1   1111 1111 1111 1111 1111 1111 1111
~CAPACITY取反结果		111  0  0000 0000 0000 0000 0000 0000 0000 (前三位全为1，后29位全为0)
c的结果					111  X  XXXX XXXX XXXX XXXX XXXX XXXX XXXX (由上诉可知RUNNING高3位值是111)
c & ~CAPACITY的结果		111  0  0000 0000 0000 0000 0000 0000 0000 (与RUNNING对应的结果一致)
1
2
3
4
5

获取线程数量

我们以2个线程数来举例

CAPACITY结果			000 1 1111 1111 1111 1111 1111 1111 1111
2的二进制表示			XXX 0 0000 0000 0000 0000 0000 0000 0010
c & CAPACITY的结果		000 0 0000 0000 0000 0000 0000 0000 0010
1
2
3

打包函数

// rs 运行状态
// wc 工作线程个数
private static int ctlOf(int rs, int wc) { return rs | wc; }
1
2
3

对 runState 和 workerCount 进行 | (按位或)操作来得到 ctl 变量
就是因为 runState 的高 3 位为有效信息，而 workerCount 的低 29 位为有效信息，合起来正好得到一个含 32 位有效信息的整型变量。

为什么之前提到的生命周期常量要在 -1 ~ 3 的基础上再左移 29 位，因为不在常量初始化处左移的话就要在拆包/打包的时候右移来保证取到的是正确的数值。然而拆包/打包操作是要经常进行的，而常量的初始化只有一次。两下对比，明显在初始化时左移是效率更高的选择。

引用文章

详解Java线程池的ctl(线程池控制状态)【源码分析】
线程池(二、ctl 的设计分析)
一文读懂线程池的实现原理