-
机器学习入门(六)神经网络初识
目录
一、模型解释
1.1 用人脑解释
 神经网络是模拟人的神经元,通过输入电化学信号(Input:Dendrite)经过细胞核(Dealing:Nucleus)处理得到结果(Output:Axon)传给下一个神经元(下一个输入)。
神经网络是模拟人的神经元,通过输入电化学信号(Input:Dendrite)经过细胞核(Dealing:Nucleus)处理得到结果(Output:Axon)传给下一个神经元(下一个输入)。1.2 用模型解释

这个相比于人脑神经元系统:我们拿肿瘤分类举例
偏置单元(bias unit):

待训练参数:

输入(Input):
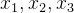
处理函数(Dealing):激活函数,逻辑回归的激活函数为Sigmoid函数

输出(Output):根据处理函数处理出的值和判断阈值确定分类或者输出逻辑是或者逻辑否。

神经网络一般有三层:分别是输入层、隐藏层和输出层。
 我们定义几个符号:
我们定义几个符号: :是第
:是第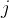 层的第
层的第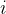 个激活单元
个激活单元  :控制从层
:控制从层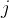 到层
到层 的函数映射的权重矩阵
的函数映射的权重矩阵
且一般每新的一个隐藏层会多一个隐藏层,如果用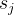 表示在
表示在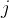 层的单元数量,
层的单元数量, 表示在
表示在 层的单元数量,那么
层的单元数量,那么 的维度为
的维度为 。
。二、通过异或门的神经网络理解偏置量、神经网络的传播
2.1 与门的神经网络表示
这里我们选择单层隐藏层的神经网络,假设我们训练出的参数
 为20,20。(怎么训练的不用管,后文会介绍)。偏置量
为20,20。(怎么训练的不用管,后文会介绍)。偏置量 设置为30。
设置为30。我们输入为
 ,输出为
,输出为
神经网络如下:

①我们输入一组参数判断是否是与逻辑,比如

则激活函数
 ,通过观察Sigmoid函数:
,通过观察Sigmoid函数:
 的值低于0.01,远低于0.5,我们认为是约等于0的。也就是不存在与关系。
的值低于0.01,远低于0.5,我们认为是约等于0的。也就是不存在与关系。②我们输入一组参数判断是否是与逻辑,比如

则激活函数
 ,通过观察Sigmoid函数:
,通过观察Sigmoid函数:
 的值接近于1,我们认为存在与关系。
的值接近于1,我们认为存在与关系。2.2 或门的神经网络表示
这里我们选择单层隐藏层的神经网络,假设我们训练出的参数
 为20,20。(怎么训练的不用管,后文会介绍)。偏置量
为20,20。(怎么训练的不用管,后文会介绍)。偏置量 设置为-10。
设置为-10。我们输入为
 ,输出为
,输出为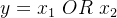
神经网络如下:

①我们输入一组参数判断是否是与逻辑,比如

则激活函数
 ,通过观察Sigmoid函数:
,通过观察Sigmoid函数:
 的值接近于1,我们认为存在或关系。
的值接近于1,我们认为存在或关系。②我们输入一组参数判断是否是与逻辑,比如

则激活函数
 ,通过观察Sigmoid函数:
,通过观察Sigmoid函数:
 的值接近于1,我们认为存在与关系。
的值接近于1,我们认为存在与关系。2.3 异或门的神经网络表示
我们结合与门和非门,推导出异或门。
异或门对应两种情况:

 对应的情况是
对应的情况是
 对应的情况是
对应的情况是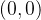
则去掉这两种情况便得到了异或门。我们画出神经网络的结构:

推导前面已经给出,现不重复推导。
三、多物体分类

神经网络也能进行多物体分类,它的输出层为向量,如果确定是该物体则该向量的该分量输出为1,而不是像1,2,3,4之类的。
-
相关阅读:
Qt quick性能提升[通俗易懂]
Falcon-7B大型语言模型在心理健康对话数据集上使用QLoRA进行微调
基于Hadoop的MapReduce网站日志大数据分析(含预处理MapReduce程序、hdfs、flume、sqoop、hive、mysql、hbase组件、echarts)
Node.js+vue+mysql高校人事管理系统7sgv0
第二章、dubbo 框架(直连方式 dubbo)
在spring中使用Validated和@Valid对参数进行校验
动态密码 作为程序员之网络安全一定要看
虚拟磁盘discard在qemu中的应用
【JAVA】值传递与引用传递
jupyter notebook
- 原文地址:https://blog.csdn.net/qq_41694024/article/details/127730224