Python动态演示旋转矩阵的作用

先新建一组散点充当坐标轴

为了比较直观地展示旋转过程，这里通过散点来新建三个坐标轴，通过对这三个坐标轴的转动，来直观地展现转动矩阵对坐标变换的影响。

import numpy as np
import matplotlib.pyplot as plt

def setAxis(N, axis=0):
    xs = np.arange(N)
    ys = np.zeros_like(xs)
    zs = np.zeros_like(xs)
    if axis==0 : return [xs, ys, zs]
    elif axis==1 : return [ys, xs, zs]
    else: return [ys, zs, xs]

def drawAxis(X,Y,Z):
    ax = plt.subplot(projection='3d')
    ax.scatter(*X, c='r')
    ax.scatter(*Y, c='g')
    ax.scatter(*Z, c='b')
    plt.show()

X = setAxis(10, 0)
Y = setAxis(10, 1)
Z = setAxis(10, 2)    
drawAxis(X, Y, Z)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

效果为

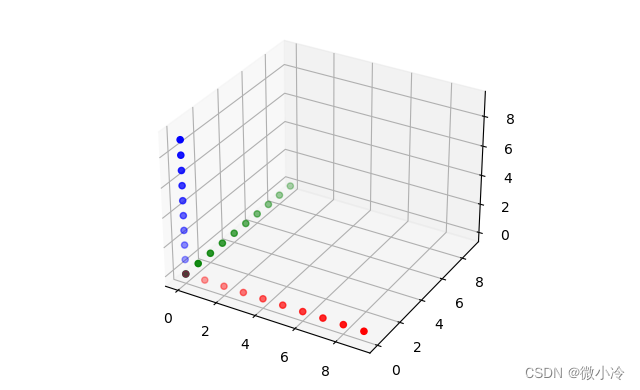
旋转矩阵与初步演示

欧拉角是用来唯一地确定定点转动刚体位置的三个一组独立角参量，由章动角θ、进动角ψ和自转角φ组成，为L.欧拉首先提出，故得名。

为了尽快进入演示部分，故对原理的介绍从略，仅从二维平面上的旋转矩阵出发，做一个简单的推导，而三维旋转矩阵，至少在形式上与二维是雷同的。

假设坐标系中有一个向量$(x,y)$，其模长为$r=\sqrt{x^2+y^2}$，角度为${\theta }_0=\arctan \frac{y}{x}$。若将其围绕坐标原点逆时针旋转$\theta$，则其坐标变为

$$\begin{gathered} x^{\prime }=r\cos ({\theta }_0+\theta )=r\cos {\theta }_0\cos \theta -r\sin {\theta }_0\sin \theta \\ {y}^{\prime }=r\sin ({\theta }_0+\theta )=r\sin {\theta }_0\cos \theta +r\cos {\theta }_0\sin \theta \end{gathered}$$

由于$x=r\cos {\theta }_0,y=r\sin {\theta }_0$，则上式可以写为

$$\begin{gathered} x^{\prime }=x\cos \theta -y\sin \theta \\ {y}^{\prime }=-x\sin \theta +y\cos \theta \end{gathered}$$

写成矩阵形式即为

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

也就是说，在平面直角坐标系上，向量绕原点顺时针旋转$\theta$，相当于左乘一个旋转矩阵。

推广到三维，为了限制$xy$坐标平面上的旋转，要将其旋转中心从原点扩展为绕着$z$轴旋转，从而三维旋转矩阵可推广为

$$\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]$$

同理可得到绕三个轴转动的旋转矩阵，为了书写方便，记$S_{\theta }=\sin \theta ,C_{\theta }=\cos \theta$，可列出下表。

下面用lambda表达式来实现，用以描述单个轴的旋转过程。

import numpy as np
# 将角度转弧度后再求余弦
cos = lambda th : np.cos(np.deg2rad(th))
sin = lambda th : np.sin(np.deg2rad(th))

# 即 Rx(th) => Matrix
Rx = lambda th : np.array([
    [1, 0,       0],
    [0, cos(th), -sin(th)],
    [0, sin(th), cos(th)]])
Ry = lambda th : np.array([
    [cos(th),  0, sin(th)],
    [0      ,  1, 0],
    [-sin(th), 0, cos(th)]
])
Rz = lambda th : np.array([
    [cos(th) , sin(th), 0],
    [-sin(th), cos(th), 0],
    [0       , 0,       1]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

有了旋转矩阵，就可以旋转，接下来让坐标轴沿着三个轴分别旋转30°，其效果如下

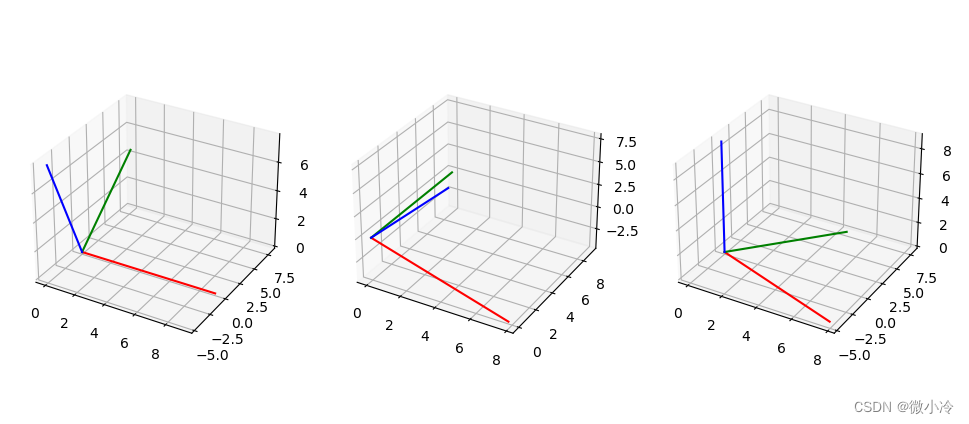
代码如下

def drawAxis(X, Y, Z, fig, i):
    ax = fig.add_subplot(1,3,i,projection='3d')
    ax.plot(*X, c='r')
    ax.plot(*Y, c='g')
    ax.plot(*Z, c='b')

Xx, Yx, Zx = Rx(30) @ X, Rx(30) @ Y, Rx(30) @ Z
Xy, Yy, Zy = Ry(30) @ X, Ry(30) @ Y, Ry(30) @ Z
Xz, Yz, Zz = Rz(30) @ X, Rz(30) @ Y, Rz(30) @ Z

fig = plt.figure("rotate")
drawAxis(Xx, Yx, Zx, fig, 1)
drawAxis(Xy, Yy, Zy, fig, 2)
drawAxis(Xz, Yz, Zz, fig, 3)

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

转动次序对旋转的影响

由于旋转被建模成了矩阵，而众所周知矩阵乘法是不可交换的，也就是说，就算绕着三个坐标轴旋转相同的角度，也会因为转动次序不同而引发不同的结果。

XYZ = [X, Y, Z]
R_xyz = [Rz(30) @ Ry(30) @ Rx(30) @ R for R in XYZ]
R_zyx = [Rx(30) @ Ry(30) @ Rz(30) @ R for R in XYZ]
R_yxz = [Rz(30) @ Rx(30) @ Ry(30) @ R for R in XYZ]

fig = plt.figure("rotate")
drawAxis(*R_xyz, fig, 1)
drawAxis(*R_zyx, fig, 2)
drawAxis(*R_yxz, fig, 3)

plt.show()
1
2
3
4
5
6
7
8
9
10
11

得到下图

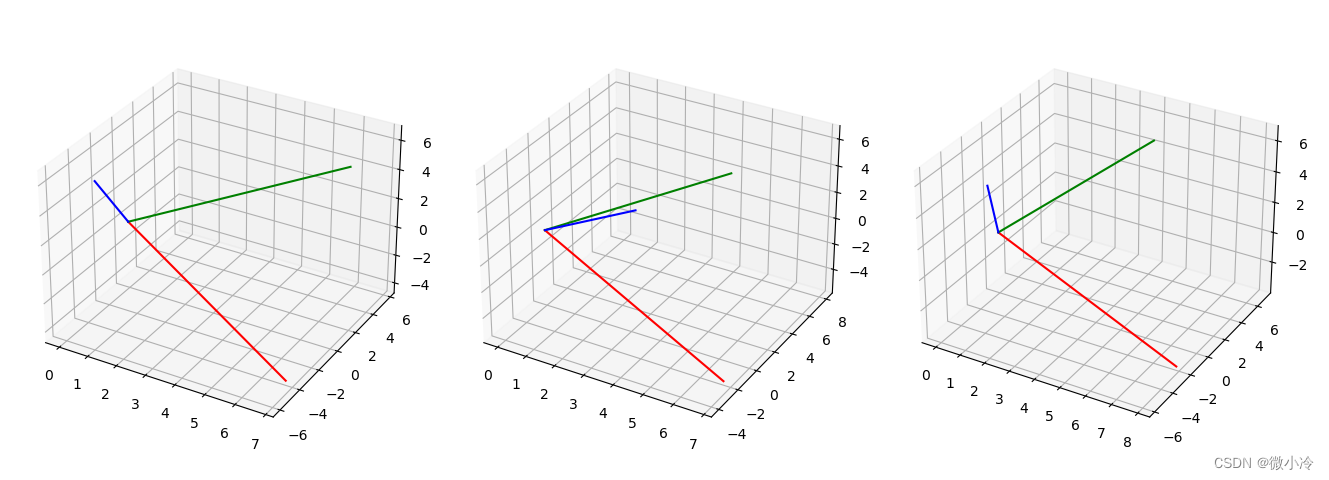
动态演示旋转过程

30°的转动之后，坐标轴变得面目全非，接下来要做的就是动态绘制这三个坐标轴的旋转过程

from numpy.random import rand
from matplotlib import animation

Rot = [Rx, Ry, Rz]
# 根据指定坐标轴顺序来以指定角度旋转向量
def rotVec(vec, axis, degs):
    for i in range(len(axis)):
        vec = Rot[axis[i]](degs[i]) @ vec
    return vec

# 若x在[a,b]区间，则对a取模，若小于a置0，大于b为b-a
def truncMod(x, a, b):
    if x < a : return 0
    elif x >= b : return b-a
    else : return x%(b-a)

# 三个坐标轴
XYZ = [setAxis(10,i) for i in range(3)]

fig = plt.figure(figsize=(5,5))
ax = fig.add_subplot(projection='3d')
ax.grid()

lines = [ax.plot([],[],[], '-', lw=0.5, c=c)[0] 
    for c in 'rgb']

def animate(n):
    # 按照xyz顺序旋转
    axis = [2,1,0]
    degs = [truncMod(n, st, st + 30) for st in [0,30,60]]
    newXYZ = [rotVec(x, axis, degs) for x in XYZ]
    for i in range(3):
        lines[i].set_data(newXYZ[i][0],newXYZ[i][1])
        lines[i].set_3d_properties(newXYZ[i][2])
    return lines

ani = animation.FuncAnimation(fig, animate, 
    range(90), interval=50, blit=True)

#plt.show()
ani.save("zyx.gif")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

效果如下