python机器人编程——基于单目视觉、固定场景下的自动泊车（上）

一、前言

本篇来讨论一下在固定场景下，如何仅通过单目视觉，实现差速小车的自动停靠，这种方式实现成本比较低，可适应的范围比较广，比如可以应用于小车的自动充电桩寻找、工位的最准等应用场景。我们还是尝试应用有限、浅显的数学对固定场景下，通过坐标的变换、几何的分析、结合单目摄像头获取的图像，进行相机位置（或者小车的位置）的估计，并控制差速小车行驶至我们预设的位置停靠。本篇先来构建小车位置的估计。

二、主要原理

（1）固定场景假设

这里我们研究的场景不是室外或者开放环境的场景，我们对场景进行适当的简化，减少其它因素的影响，设置的场景是这样的，我们在墙上贴上三个二维码，充当人工的特征点，然后假设地面是水平的，相机固定在小车的正上方，朝向小车正前向位置。这样一来，可以知道，小车的运动，前后左右移动和转向，摄像头也跟着运动，且运动的自由度只有3个，即：
如图，相机在“相机运动平面”内运动（固定高度的平面内位置改变，只有xw，yw的变化），在运动平面内，随着小车的转向，相机沿着自身YC轴旋转，其它轴没有旋转运动。

如上图，我们约定目标位置（如停靠的车位）在O点，当前位置在A点，我们的任务就是根据当前获取的的图像和O点位置获取的图像进行对比计算，计算出A点相对于O点的位置。知道位置后，就可以生成一条运动轨迹线，这样就可以控制小车移动到目标点O。

（2）相机位置关系分析

1）一般坐标变换关系

由相机的成像原理（主要是指小孔成像、相似原理），和三维坐标变换原理（主要是指三维坐标系的沿着x、y、z轴的移动和旋转），我们知道将一个在现实世界中的实物点（xw,yw,zw）投影到相机的照片图像上的一个点(u、v)，需要经过一系列的坐标变换得到（由于这方面网上资料众多，这里不再赘述）：

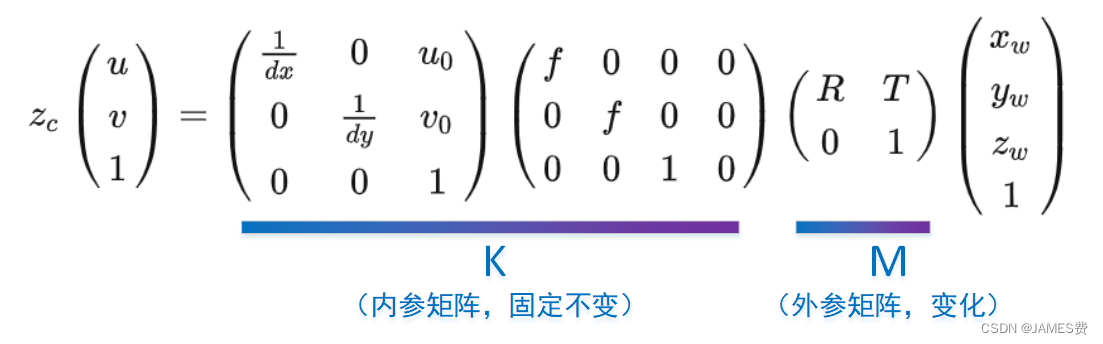
其中：
dx:图像中每个像素 x 轴的物理尺寸，单位：mm/pix
dy:图像中每个像素 y 轴的物理尺寸，单位：mm/pix
u0：图像的原点（中心）像素坐标u，单位:pix
v0：图像的原点（中心）像素坐标v，单位:pix
f：相机中心到成像平面的垂直距离(或焦距),单位：mm
R: 从世界坐标系到相机坐标系的旋转变换矩阵，是分别绕三个轴旋转矩阵的乘积，绕三个轴旋转的矩阵分别为：

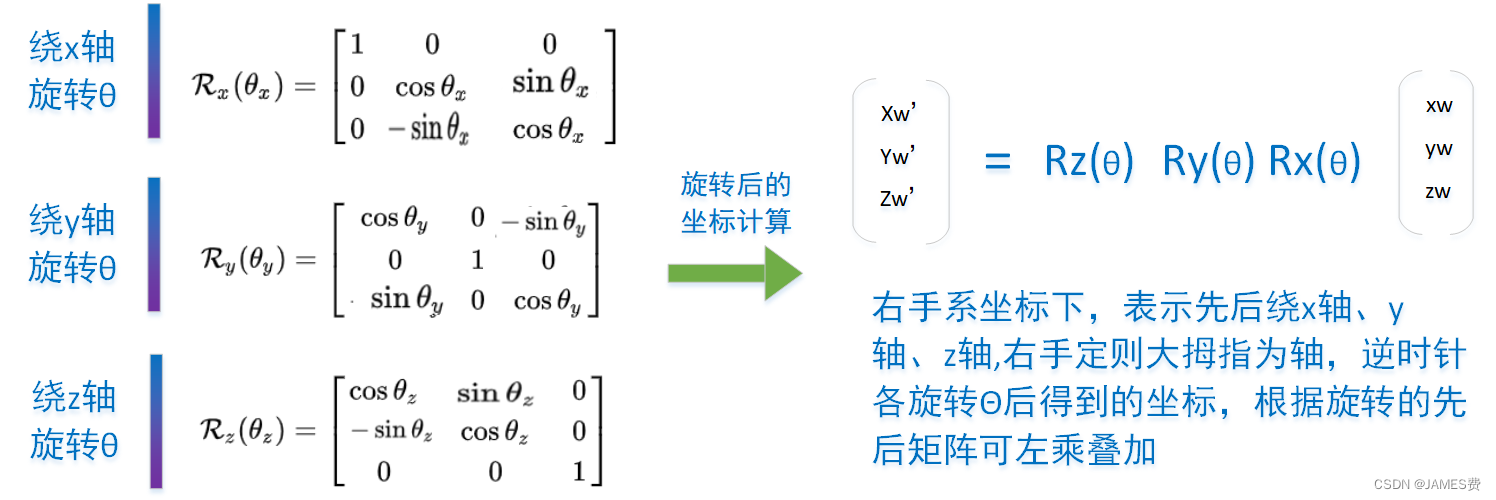
注意：此处为右手系坐标，顺逆符合右手定则
T：从世界坐标系到相机坐标系的平移变换（x、y、z方向的增减）：

Zc:表示点在相机坐标系的z方向的坐标值，单位：mm。
K：表示相机的内参矩阵：

根据以上的关系，我们在同一个相机不同位置看到的同一个点，在图像上表现为u、v的位置不同，那么在本篇的固定场景中，我们分别在O、A两个位置观察P0点，得到的图像计算如下：

然而，我们本次要解决的问题是，A位置如何运动到O位置的问题（或者是O位置如何运动到A位置的问题），如果我们设从O位置到A位置的运动（旋转、平移）的变换矩阵为M2，则利用从以上运算我们可以容易得出，一下关系：

M3是可以分解为两步运算的，然后再可以看出，等式右边部分，其实是就是跟O位置的相关的：

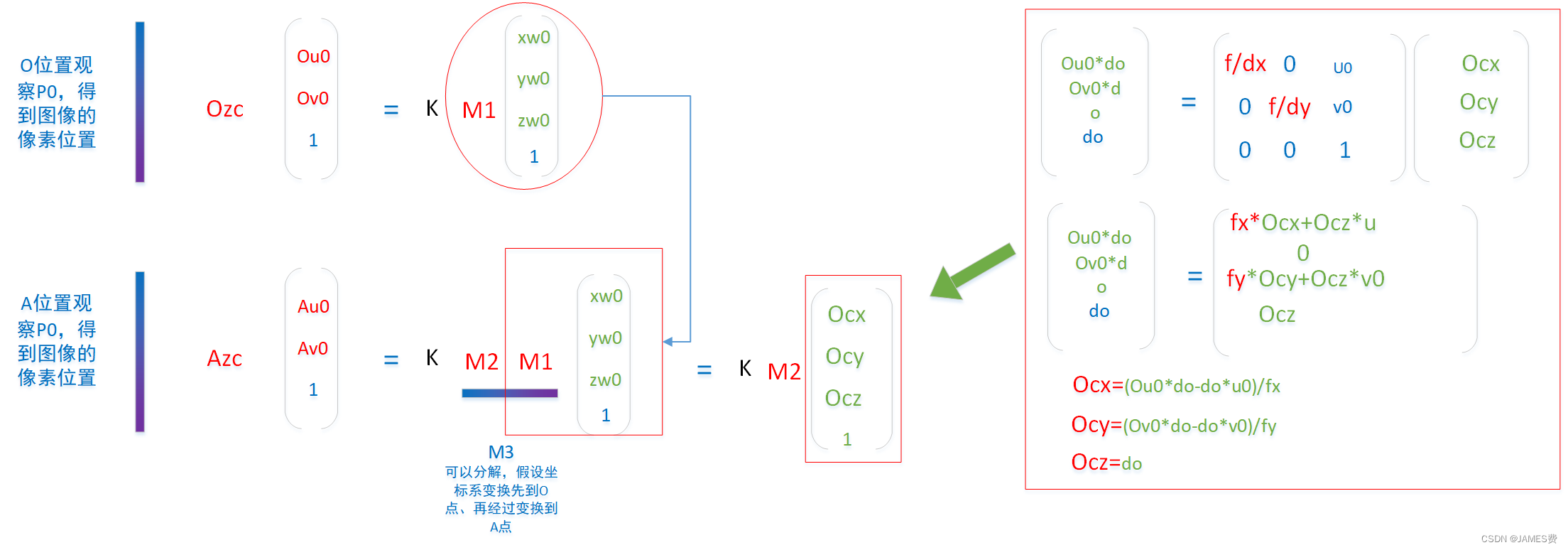
到此，我们可以大概看出，要解决本篇的目标（求M2），是可以通过观察比较两个位置的图像上的成像点的像素坐标，经过一些列计算得到的。

2）三自由度下的变换关系

（1）P0到O的运动，M1

由于O点位置我们是已知的，运动也是已知的，从图可以看出，从P0点到O点位置运动，就是世界坐标系平移旋转后到相机坐标系O的过程：即，先沿着坐标yw的负方向平移5000mm，然后绕xw轴旋转270°即为O系坐标：

这样已知M1，和坐标点，我们在不考虑畸变的情况下，可以对不知道相机内参的相机，进行简单“标定”，求出内参K：

通过以上方程，可知K里面有3个未知数，那么其实可以带入已知的2个点P0，P1获取图像的像素点坐标，就可以解出内参的数值。这其实也是简化的相机标定原理！
经过推导可得到如下算式（令fx=f/dx,fy=f/dy）：

python程序

根据以上公式，我们就可以做一个函数，实现根据初始位置图像的计算相机K参数：

def sovle_K_byimg(img,P0,tagid=1,do=5000):
    """
    根据已知0位图，和t时刻图计算当前位置    
    P0: 固定标签点的世界坐标(x,y,z)
    """
    H=img.shape[0]
    W=img.shape[1]
    u0=W/2
    v0=H/2
    (xw0,yw0,zw0)=P0
    #获取特征点的像素坐标
    res,tagcenter=apritap(img,multple=0,tagid=tagid)
    if res:       
        Ou0=tagcenter[0]
        Ov0=tagcenter[1]
        print("tag center:",Ou0,Ov0)
        if xw0 and zw0:            
            fx=(Ou0*(do+yw0)-u0*(do+yw0))/xw0
            fy=-(Ov0*(do+yw0)-v0*(do+yw0))/zw0  
            return True,fx,fy
        else:
            print("sovle_K_byimg:P0 x,z not be zero")
            return False,0,0
             
        
    else:
        print("sovle_K_byimg failed")
        return False,None,None
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

计算结果如下：

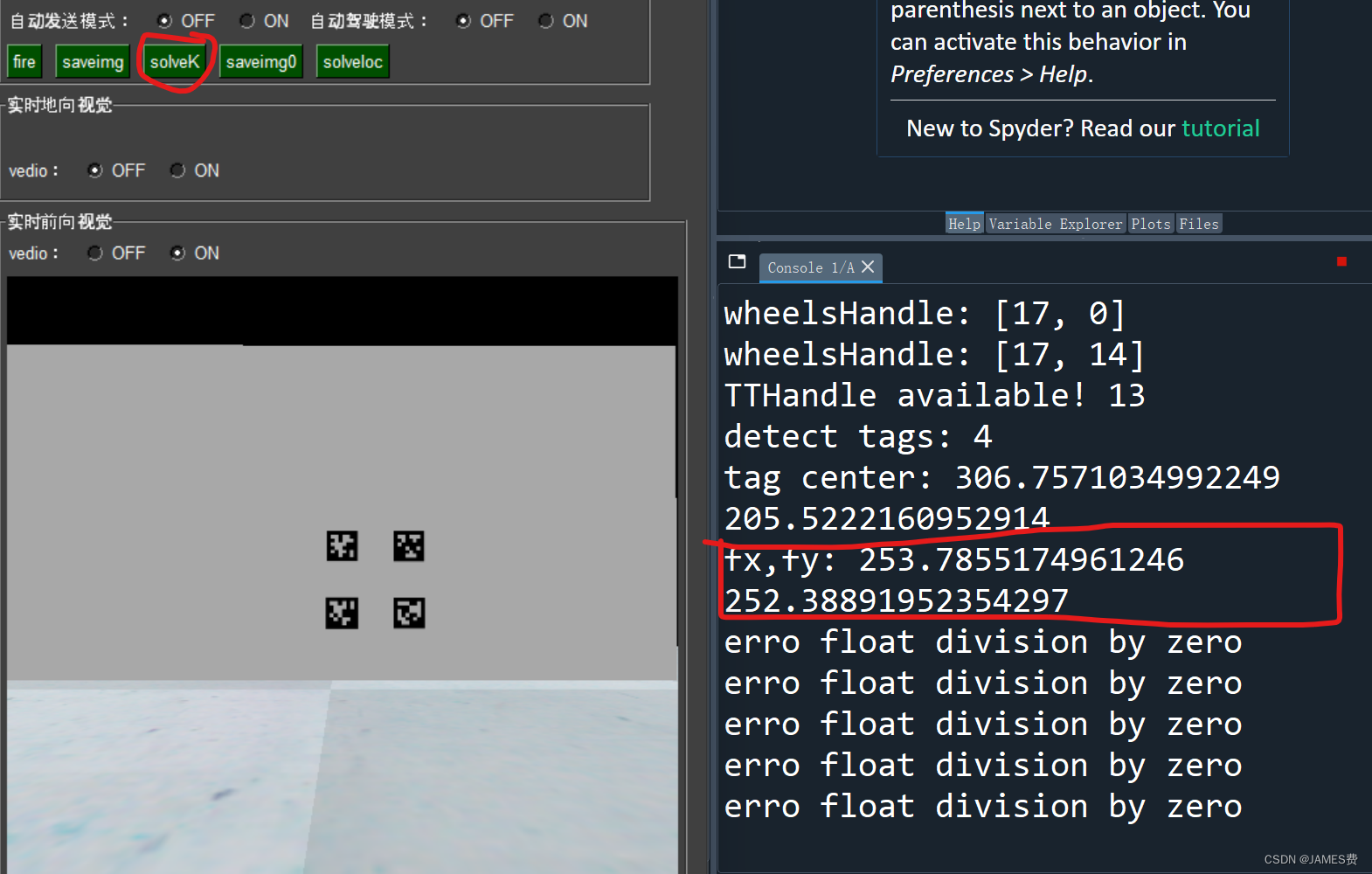
可以看到，由于识别的二维码位置有误差，计算出来的fx、fy会有误差，实际，在仿真环境，摄像头为理想模型无畸变，其参数为fx=256,fy=256。

（2）O到A位的运动，M2

在本项目中，由于我们简化了场景，事实上，小车运动是在一个二维平面的，相机也是如此，在一个二维平面做平移运动，同时只沿着yc轴做旋转运动，其它自由度的运动都为0，这样一来就大大减少了所要求解的参数。
O到A运动，涉及的旋转矩阵其实只有一个Ry(θ)

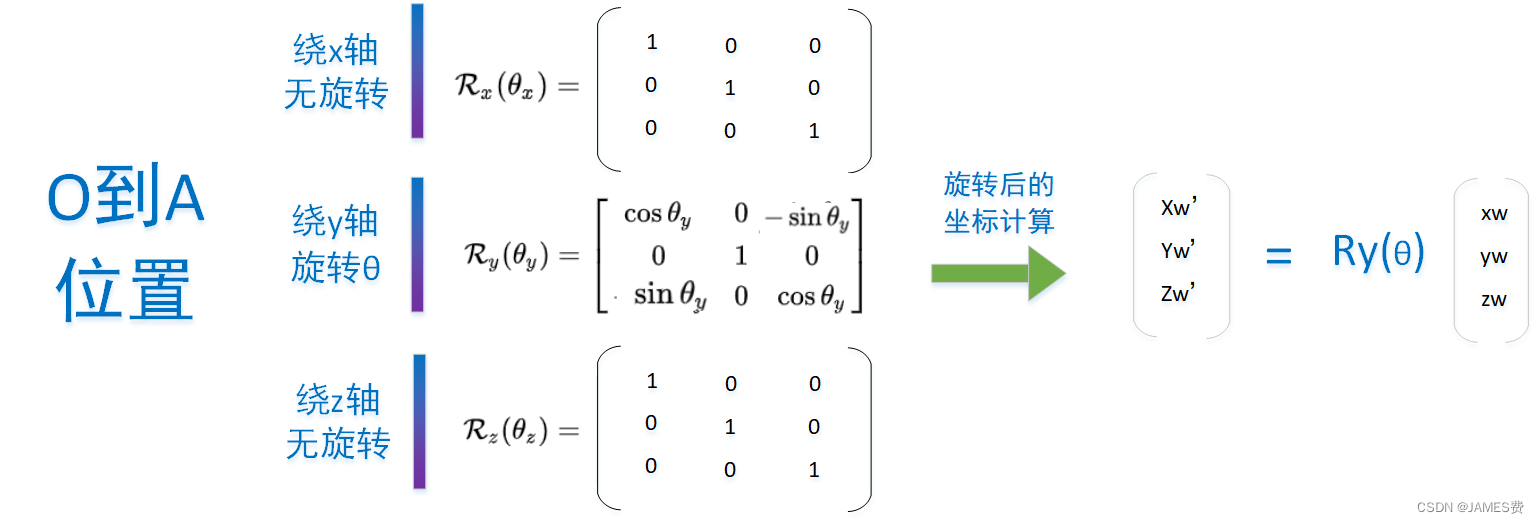
然后其平移也只是在相机坐标轴z、x方向的变化，那么结合上面的公式可以列出方程组：

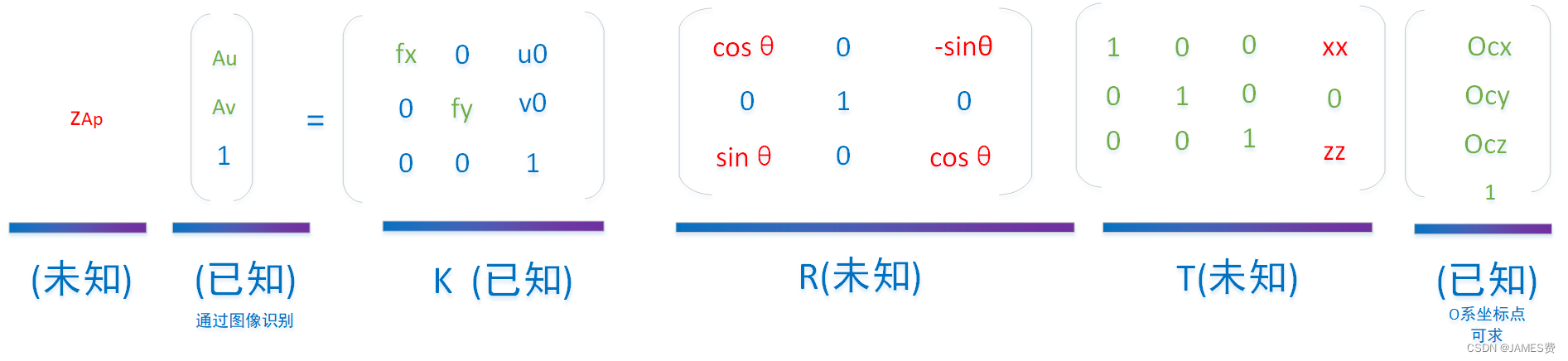
从上面方程组可以看出，本固定场景下，要求的相机位置A涉及未知数（xx，zz）和θ，要求出这些未知数，只要代入足够多的已知点，就可以解出方程。方程推导如下：

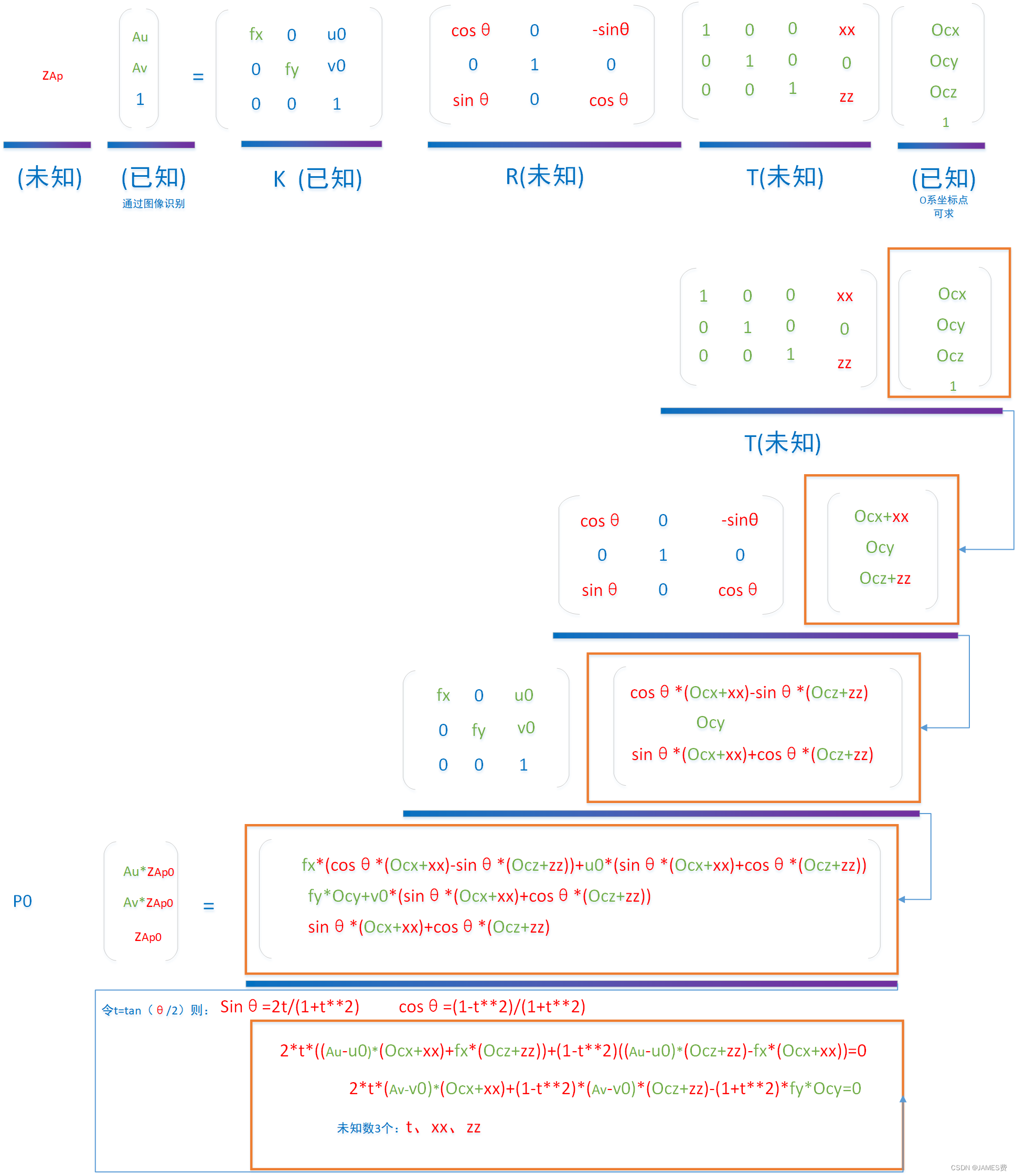
从上面可知，未知数有3个，但是只有二个方程组，为超定方程组，我们可以通过加入其它固定点的信息，利用最小二乘法求解未知数。

下面我们来编程实现一下：

python编程

        #构建方程组（部分代码）        
    def solve_f(xn):
        """
        解方程组

        """

        t,xx,zz=xn
 
        equations="[" 
        
        for i in Pnum: 
            equations=equations+"2*t*((Au"+str(i)+"-u0)*(Ocx"+str(i)+"+xx)+fx*(Ocz"+str(i)+"+zz))+(1-t**2)*((Au"+str(i)+"-u0)*(Ocz"+str(i)+"+zz)-fx*(Ocx"+str(i)+"+xx)),"
            equations=equations+"2*t*(Av"+str(i)+"-v0)*(Ocx"+str(i)+"+xx)+(1-t**2)*(Av"+str(i)+"-v0)*(Ocz"+str(i)+"+zz)-(1+t**2)*fy*Ocy"+str(i)+","

        equations=equations[:-1]+"]"
        return eval(equations)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

运行结果如下：

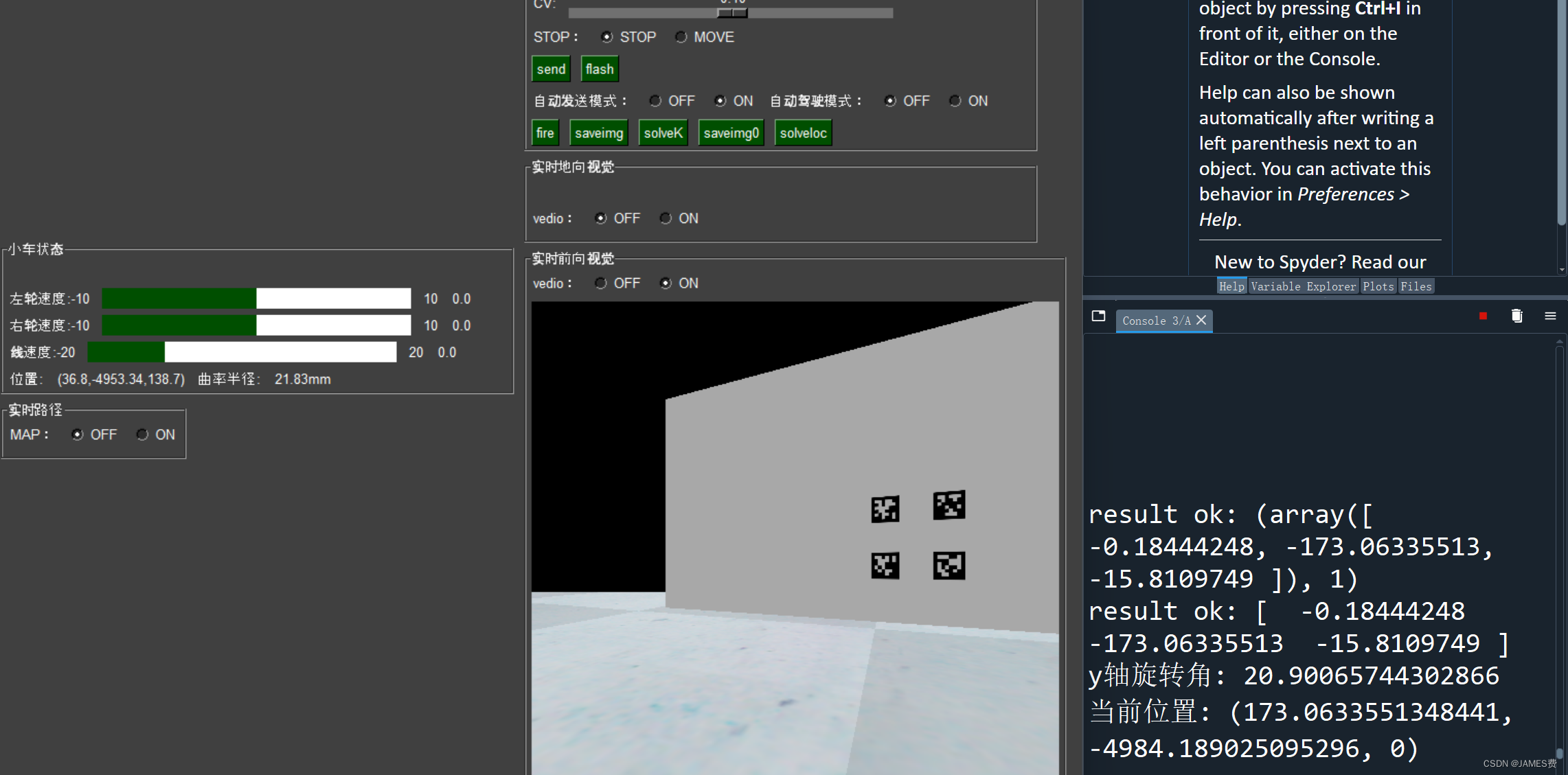
以上算法有一定的误差，我这里只用到了3个特征点，实际应用中需要进行多个采样点，并使用优化算法进行非线性优化。

四、上篇总结

这样，在固定场景下，以及相机为理想模型下，我们通过对相机成像原理模型，构建了本项目所需的位置估计算法。实际应用中，相机的内参可以通过相机标定方法进行标定获得，由于存在视觉误差，且需要对相机位置的估计进行必要的优化，或者装设激光雷达等其它传感进行多源信息的校核。
下篇我们基于本篇的位置信息，来进一步实现小车的自动控制。