初学者看 “图“

环(loop):如果图含有一条从顶点到它自身的边(v,w),该path也称作环

强连通:如果无向图从每一个顶点出发到每个其他顶点都存在一条路径。

弱联通：如果有向图不是强连通，但是他的基础图（去掉边上方向所形成的图）是连通的。

完全图：是其每一对顶点都存在一条边的图

2.现实模拟

如果任一顶点代表机场，边表示的机场间如果存在一条直达航线，那么这两个顶点就用一条边连接。边可以有一个权，表示时间、距离或飞行的费用。有理由假设，这样的一个图是有向图，因为在不同的方向上飞行可能所用时间或所花的费用会不同（例如，依赖于地方税)。可能我们更希望航空系统是强连接的，这样就总能够从任一机场飞到另外的任意一个机场。我们也可能愿意迅速确定任意两个机场之间的最佳航线。“最佳”可以是指最少边数的路径，也可以是对一种或所有权重量度所算出的最佳者。

2.图的表示

1.考虑有向图

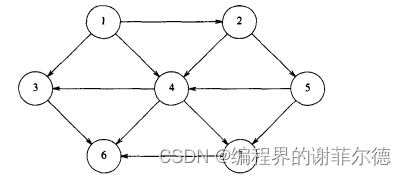
2.adjacent matrix(dense)

表示图的一种简单方法是使用二维数组，称为邻接矩阵（ adjacent matrix）表示法。对于每条边(u, v)，置A[u][v] = true;否则,数组的项就是false。如果边有一个权，那么可以置A[u] [v]等于该权，而使用一个很大或者很小的权作为标记表示不存在的边。例如，如果要寻找最便宜的航空路线，那么可以用值0来表示不存在的航线。如果出于某种原因要寻找最昂贵的航线，那么可以用无穷(或者使用0)来表示不存在的边。

虽然这种表示的优点是非常简单，但是，它的空间需求则为O(|V|2)，如果图的边不是很多，那么这种表示的代价就太大了。若图是稠密的(dense):E = O(|V|2)，则邻接矩阵是合适的表示方法。不过，在我们将要看到的大部分应用中，情况并不如此。例如，设用图表示一个街道地图，街道呈曼哈顿式，其中几乎所有的街道或者南北向、或者东西向。因此，任一路口大致都有四条街道，于是，如果图是有向图且所有的街道都是双向的，则E=4V。如果有3000个路口，那么就得到一个3000顶点的图，该图有12 000条边，它们需要一个大小为9 000 000的数组。该数组的大部分项将是0。这从直观来看很糟，因为我们想要数据结构表示那些实际存在的数据，而不是去表示不存在的数据。

3.adjacent list(SPARSE稀疏)

对每一个顶点，我们使用一个表存放所有邻接的顶点。此时的空间需求为O(|E|+|V|),

它相对于图的大小而言是线性的'。最左边的结构只是头单元(header cell)的数组。这种表示方法从可以清楚地看出。如果边有权，那么这个附加的信息也可以存储在单元中。

 邻接表是表示图的标准方法。无向图可以类似地表示;每条边(u,v)出现在两个表中，因此空间的使用基本上是双倍的。在图论算法中通常需要找出与某个给定顶点v邻接的所有的顶点。而这可以通过简单地扫描相应的邻接表来完成，所用时间与这些找到的顶点的个数成正比。

有很多方法可以维护邻接表。首先，要注意到这些表自身可以通过vector或list来维护。然而，对于稀疏图，当使用vector时，程序员需要将每一个vector都初始化为比默认值稍小一-点的容量，否则就会浪费大量的空间。

由于快速得到任何顶点的邻接顶点列表很重要,所以有两个基本的选择:或者使用图(map)，其键为顶点，值为邻接表，或者将每个邻接表作为vertex类的成员函数处理。第一个选择似乎简单些，但是第二个选择更快，因为避免了在图中的重复查找。

对第二种情况，如果顶点是string （例如机场的名字或者路口的名字)，那么可以使用图。其中，键是顶点的名字，值是vertex（典型的是一个指向vertex的指针)，并且每一个vertex对象都有一个邻接顶点（指向顶点的指针）的列表，可能还包括原始的string名。

3. 拓扑排序

拓扑排序( topological sort）是对有向无环图的顶点的--种排序，它使得如果存在--条从vj到vi,的路径，那么在排序中vi出现在vj,的后面。下图表示了迈阿密州立大学的课程结构。有向边(v, w)表明课程v必须在课程w选修前修完。这些课程的拓扑排序不会破坏课程结构要求的任意课程序列。

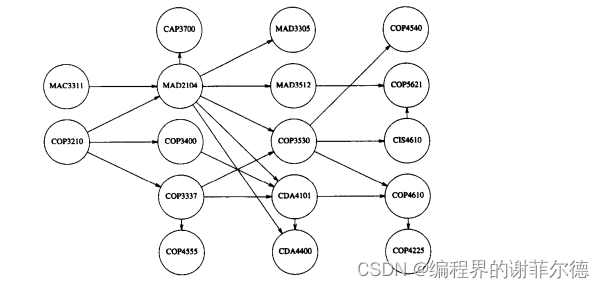
 一个简单的求拓扑排序的算法是先找出任意一个没有入边的顶点。然后显示出该顶点，并将它和它的边一起从图中删除。然后，对图的其余部分应用同样的方法处理。

为了将上述方法公式化，我们把顶点v的入度( indegree）定义为边(u,v)的条数。计算图中所有顶点的入度。假设每一个顶点的入度被存储且图被读入一个邻接表中。

1. FindInDegree()函数的实现：

FindInDegree()函数的实现思路：
1：定义两层循环遍历整个邻接表
2：定义指向各个边结点的指针，
此指针从指向某结点链表的第一个邻接点开始，遍历整个顶点链表，
当某边结点邻接点域等于i时，计数变量自增
3：邻接表遍历结束后，将计数变量的值赋予indegree[i]数组单元

void FindInDegree(ALGraph G, int indegree[]) {
	for (int i = 0; i < G.vexnum; i++) {
		int cnt = 0;//设置变量存储邻接点域为i的结点个数
		for (int j = 0; j < G.vexnum; j++) {
			ArcNode* p = new ArcNode;//定义指向各个边结点的指针
			p = G.vertices[j].firstarc;
			while (p) {//当p未指到单个链表的末尾时继续循环
				if (p->adjvex == i)//当某边结点邻接点域等于i时，计数变量++
					cnt++;
				p = p->nextarc;//指针不断向后指
			}
			indegree[i] = cnt;//将计数结果保留在indegree数组中
		}
	}
}

 2.拓扑排序实现

拓扑排序算法思路：
1：求出各结点的入度存入数组indegree中
2：遍历indegree[i]数组，将单元值为0的编号值i进栈
3：将栈顶元素保存在topo数组中，并将此元素出栈。
4：定义指向边结点的指针，使该指针从出栈元素的第一个边结点开始依次向后指，遍历某顶点元素的所有边结点，并将每个边结点对应的indegree数组单元值自减，当indegree单元值为0时，将该边结点邻接点域进栈
5：最后将m和有向图顶点比较，若两者相等，则该图是有向无环图。

Status TopologicalSort(ALGraph G, int topo[]) {
	//有向图G采用邻接表存储结构
	//若G无回路，则生成G的一个拓扑排序topo[]并返回OK，否则ERROR
	FindInDegree(G, indegree);//求出各结点的入度存入数组indegree中
	SqStack S;
	InitStack(S);//初始化栈
	for (int i = 0; i < G.vexnum; i++) {
		if (!indegree[i]) Push(S, i);//入度为0者进栈
	}
	int m = 0;//对输出顶点计数u，初始为0
	while (!StackEmpty(S)) {
		int i = 0;
		Pop(S, i);//将栈顶顶点vi出栈
		topo[m] = i;//将vi保存在拓扑序列数组topo中
		++m;//对输出顶点计数
		ArcNode* p = new ArcNode;
		p = G.vertices[i].firstarc;//p指向vi的第一个邻接点
		while (p != NULL) {
			int k = p->adjvex;//vk为vi的邻接点
			--indegree[k];//vi的每个邻接点的入度减一
			if (indegree[k] == 0) Push(S, k);//若入度减为0，则入栈
			p = p->nextarc;//p指向顶点vi下一个邻接结点
		}
	}
	if (m < G.vexnum) return ERROR;//该有向图有回路
	else return OK;
}