-
高阶数据结构—— 哈希
前言： 哈希是一种很高效的存储数据的结构，它是利用的一种映射关系，它也是STL中unordered_map和unordered_set 的底层结构。本文，主要讲解哈希的原理，哈希的实现，里面关键点在于如何解决哈希冲突。
1.哈希概念
哈希其实在学排序时已经用过了，就是计数排序。计数排序也是用的一种映射关系。
比如对此数组进行 计数排序 ：1 1 9 9 9 3 3 8 8
我用的是绝对映射 ，所以开辟的数组空间 它的大小 必须 能映射到 最大的元素。
但是 对于哈希来讲，可以用决定映射嘛？当然不可以，如果是绝对映射会造成很大的空间浪费。所以 哈希 用的是 取模的方式来存 数据。
比如 ： 哈希表 的空间 我给定 只能存放 10个元素
存进来的数 对10进行取模 ，那么必定可以存方到 这个哈希表中。比如：存 100 ，它对10取模得 0，那它就存在第一个位置；存 52 ，它对10进行取模得 2，那它就存到 下标为 2的位置。
也就是说 无论多大的数据，都可以存到哈希表中。但是 有两个 问题：
-
数据都能进行取模吗？假如我要求哈希表中存的是一个字符串，字符串不能进行取模运算，该怎么办？这就是数据可否哈希的问题，我们要把存进哈希表的数据，变为可哈希数据。
-
如果我存的是 4，下一次我要存的是 14。由于 4的位置已经被占了，我存的 14 该存放到何处？要是直接存，就意味着前面存的 4 会被覆盖，造成数据丢失。这就是哈希冲突问题。
2. 哈希冲突
造成了哈希冲突，得解决哈希冲突问题。
这里给出两种解决手段：
- 闭散列：也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把key存放到冲突位置中的“下一个” 空位置中去。
它相当于 如果我本来要存的位置，已经被占了，那么我就要在哈希表中找一个空位置存放。 - 开散列：开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。
这种办法是常用的，它相当于 哈希表 每个位置 都存的是一个哈希桶，如果发送哈希冲突，直接就放在哈希桶里就行了。
3. 哈希实现
- 哈希表其实就是一个数组，数组中存的是节点数据，发生哈希冲突后，采用的是往后找空位置的方法。
图解：
(1) 10 % 6 == 4,所以插入到下标为4的位置
(2) 20%6==2,插入到下标为2的位置
(3)12%6 == 0,插入到下标为0的位置。
(4)22%6 == 4，插入到下标为4的位置，发现已经有数据了，所以向后找空位置。
(5)44%6 == 2，插入到下标为2的位置，发现已经有数据了，所以向后找空位置。
- 哈希桶其实就是一个数组，数组中存的是节点链表，发生哈希冲突后，是直接插入到节点链表中。
如果是哈希桶，存放上面的数据，是什么样的呢？
图解：
它相当于把发生冲突的数据 挂在了 冲突位置的下面。
3.1 闭散列(哈希表)
#include#include using namespace std; namespace hash_table { enum status { Empty, Exist, Delete }; template<class K,class V> struct hashdate { pair<K, V> _kv; status _status = Empty; }; template<class K,class V> class close_hashtable { typedef hashdate<K, V> Node; private: vector<Node> _tables; size_t _n = 0; public: Node* find(const K& key) { if (_tables.size() == 0) return nullptr; size_t start = key % _tables.size(); size_t i = 0; size_t index = start + i; while (_tables[index]._status != Empty) { if (_tables[index]._kv.first == key && _tables[index]._status == Exist) return &_tables[index]; i++; index = start + i; index %= _tables.size(); } return nullptr; } bool erase(const K& key) { Node* ret = find(key); if (ret == nullptr) return false; ret->_status = Delete; _n -= 1; return true; } bool insert(const pair<K,V>& kv) { Node* ret = find(kv.first); if (ret) { return false; } if (_tables.size() == 0 || _n * 10 / _tables.size() >= 7) { size_t newsize = _tables.size() == 0 ? 10 : _tables.size() * 2; close_hashtable<K, V> tmp; tmp._tables.resize(newsize); for (size_t i = 0; i < _tables.size(); i++) { tmp.insert(_tables[i]._kv); } _tables.swap(tmp._tables); } size_t start = kv.first % _tables.size(); size_t i = 0; size_t index = start + i; while (_tables[index]._status == Exist) { i++; index = start + i; index %= _tables.size(); } _tables[index]._kv = kv; _tables[index]._status = Exist; _n += 1; return true; } }; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
以上就是闭散列的实现。我们来一步一步的解析以上代码。
- (1) 用枚举常量来 标记 哈希表中 每个位置的状态，状态有 空，不为空，被删除。
大家可能会对 被删除这个状态产生疑问，一个位置 不就是 有数据和没数据吗？主要是大家想 如果 直接物理上删除，把位置 状态设置为 空，那么 就会影响后面的数据。
比如：删除 5 这个数据、
直接将 5 的位置 设置为空，那么 15 这个数据 会受到影响。因为 对 哈希表大小取模后，等于 5 的 不一定只有 5，还有 15，25，35。如果 将 5位置直接设置 为 空，就相当于 后面的数据中 已经没有 15，25，35 了。具体我们往下看查找的实现。enum status { Empty, Exist, Delete };- 1
- 2
- 3
- 4
- 5
- 6
- (2) 哈希表中的数据类型，以及哈希表的底层结构
哈希表中的数据类型，是一个结构体 ，包括了 一个键值对和状态：
template<class K,class V> struct hashdate { pair<K, V> _kv; // 默认状态为空 status _status = Empty; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
哈希表的底层结构，可以是一个数组，还得有一个 无符号整数用来处理 哈希表中数据的个数：
typedef hashdate<K, V> Node; private: vector<Node> _tables; size_t _n = 0;- 1
- 2
- 3
- 4
- (3) 哈希表的查找
Node* find(const K& key) { if (_tables.size() == 0) return nullptr; size_t start = key % _tables.size(); size_t i = 0; size_t index = start + i; while (_tables[index]._status != Empty) { if (_tables[index]._kv.first == key && _tables[index]._status == Exist) return &_tables[index]; i++; index = start + i; index %= _tables.size(); } return nullptr; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
注意： while循环中，它的条件是 _tables[index]._status != Empty 说明 即使当下位置状态是 Delete 也会往后找 要查找的数据。这也解释了上文中所述。
找到了的条件是 (_tables[index]._kv.first == key && _tables[index]._status == Exist)
找到了返回 数据的地址，找不到 返回 空。
- (4) 哈希表的插入
bool insert(const pair<K,V>& kv) { // 去重 Node* ret = find(kv.first); if (ret) { return false; } // 扩容，后面讲，大家可能对这个条件有疑问 if (_tables.size() == 0 || _n * 10 / _tables.size() >= 7) { size_t newsize = _tables.size() == 0 ? 10 : _tables.size() * 2; close_hashtable<K, V> tmp; tmp._tables.resize(newsize); for (size_t i = 0; i < _tables.size(); i++) { tmp.insert(_tables[i]._kv); } _tables.swap(tmp._tables); } size_t start = kv.first % _tables.size(); size_t i = 0; size_t index = start + i; // 找空的位置 while (_tables[index]._status == Exist) { i++; index = start + i; index %= _tables.size(); } // 插入操作 _tables[index]._kv = kv; _tables[index]._status = Exist; _n += 1; return true; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
扩容是有说法的，首先我们要知道什么时候需要扩容？
- 如果为空，必然需要扩容，默认给 10 个大小即可。
- 当 有效数据个数 除以 数组大小 大于等于 0.7 时，需要扩容
其实 有效数据个数 除以 数组大小 被称为 载荷因子，当载荷因子 大于 0.7时，就说明需要扩容了。这是大佬们搞出来的，我们还需要知道，载荷因子 越大就说明 填入哈希表的元素越多，越可能发送哈希冲突。
扩容的操作，我是 创建了一个新的哈希表，然后把原表中的数据插入到新表中。这里还有一个坑，就是，可不可以 直接将旧表的数据拷贝到新表中，答案是 不行。
举个例子：
原表是 ：
新表是：
直接拷贝的话是这样的：
看图也懂了哈，扩容后的表 是需要重新插入数据，因为 位置 可能会发送改变。扩容完了，就是插入了，如果当下的位置是 Delete 或者 Eempty 那么就可以直接插入；否则就需要向后面查找空的位置，进行插入。
(5) 哈希表的删除
bool erase(const K& key) { Node* ret = find(key); if (ret == nullptr) return false; ret->_status = Delete; _n -= 1; return true; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
删除很简单，就是将那个位置的状态改为 Delete，然后有效数据个数 减一 就行了。
3.1.1 闭散列的细节
首先，上面的哈希表其实还有问题。
比如： 不是所有的数据都可以取模，这个问题，并没有解决，上面实现是 直接取模。
所以还需要实现一个 将数据转为可哈希数据的仿函数。为什么是仿函数呢？因为 数据类型较多，情况不一，这里还用到了模板特化的知识，大家坐稳扶好。
template<class K> struct Hash { size_t operator()(const K& key) { return key; } }; template<> struct Hash<string> { size_t operator()(const string& key) { size_t value = 0; for (auto ch : key) { value *= 31; value += ch; } return value; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
第二个就是模板的特化， 它的作用就是 将string对象 可以转换 成 整型(可哈希)。至于为什么每次都乘以 31 ，这也是大佬的手法，因为多次测试后发现，乘以 31 会使 哈希冲突少一些。
默认情况下，就是直接返回 key，也就是默认情况下都是可哈希的。
如果 你要哈希一个自定义对象，那么还得是用模板的特化，自己处理。
所以有了仿函数之后，我们就不必担心，传过去的数据是否能够 被哈希了，靠仿函数去处理。具体怎么用，后面会给出完整代码。
其次，还有一个问题，就是
线性探索和二次探索：大家可能对这俩词不陌生，也就是哈希表中，发生哈希冲突后，查找空位置时，是连续的查找空位置还是 平方次的跳跃的查找。
当然是二次查找更优秀一些，上面的程序用的是线性探索，也就是 那个
i++，它就是连续的往后查找。为什么呢？因为 如果是线性探索，它会比较拥挤，连续位置太多，从而引发踩踏效应，也就导致，每次来的数据，都需要去找空位置。二次探索很简单，把 i++ 变成 i =i *i。
3.1.2 优化后的闭散列
enum status { Empty, Exist, Delete }; template<class K> struct Hash { size_t operator()(const K& key) { return key; } }; template<> struct Hash<string> { size_t operator()(const string& key) { size_t value = 0; for (auto ch : key) { value *= 31; value += ch; } return value; } }; template<class K,class V> struct hashdate { pair<K, V> _kv; status _status = Empty; }; template<class K,class V,class Hashfunc = hash<K>> class close_hashtable { typedef hashdate<K, V> Node; private: vector<Node> _tables; size_t _n = 0; public: Node* find(const K& key) { if (_tables.size() == 0) return nullptr; Hashfunc hf; size_t start = hf(key)% _tables.size(); size_t i = 0; size_t index = start + i; while (_tables[index]._status != Empty) { if (_tables[index]._kv.first == key && _tables[index]._status == Exist) return &_tables[index]; i = i*i; index = start + i; index %= _tables.size(); } return nullptr; } bool erase(const K& key) { Node* ret = find(key); if (ret == nullptr) return false; ret->_status = Delete; _n -= 1; return true; } bool insert(const pair<K,V>& kv) { Node* ret = find(kv.first); if (ret) { return false; } if (_tables.size() == 0 || _n * 10 / _tables.size() >= 7) { size_t newsize = _tables.size() == 0 ? 10 : _tables.size() * 2; close_hashtable<K, V> tmp; tmp._tables.resize(newsize); for (size_t i = 0; i < _tables.size(); i++) { tmp.insert(_tables[i]._kv); } _tables.swap(tmp._tables); } Hashfunc hf; size_t start = hf(kv.first) % _tables.size(); size_t i = 0; size_t index = start + i; while (_tables[index]._status == Exist) { i = i*i; index = start + i; index %= _tables.size(); } _tables[index]._kv = kv; _tables[index]._status = Exist; _n += 1; return true; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
3.2 扩散列(哈希桶)
template<class K,class V> struct HashNode { pair<K, V> _kv; HashNode<K,V>* _next; HashNode(const pair<K, V>& kv) :_kv(kv), _next(nullptr) { } }; template<class K,class V,class Hashfunc = Hash<K>> class link_hashtable { typedef HashNode<K, V> Node; private: vector<Node*> _tables; size_t _n = 0; public: Node* find(const K& key) { if (_tables.size() == 0) return nullptr; Hashfunc hf; size_t index = hf(key) % _tables.size(); Node* cur = _tables[index]; while (cur) { if (cur->_kv.first == key) return cur; else cur = cur->_next; } return nullptr; } bool erase(const K& key) { Node* ret = find(key); if (ret == nullptr) { return false; } Hashfunc hf; size_t index = hf(key) % _tables.size(); Node* pre = nullptr; Node* cur = _tables[index]; while (cur) { Node* next = cur->_next; if (cur->_kv.first == key) { if (pre == nullptr) { _tables[index] = next; } else { pre->_next = next; } delete cur; _n -= 1; return true; } else { pre = cur; cur = next; } } return false; } bool insert(const pair<K,V>& kv) { Node* ret = find(kv.first); if (ret) { return false; } Hashfunc hf; if (_n == _tables.size()) { size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2; vector<Node*> newTables; newTables.resize(newSize); for (size_t i = 0; i < _tables.size(); ++i) { Node* cur = _tables[i]; while (cur) { Node* next = cur->_next; size_t index = hf(cur->_kv.first) % newTables.size(); // 头插 cur->_next = newTables[index]; newTables[index] = cur; cur = next; } _tables[i] = nullptr; } _tables.swap(newTables); } size_t index = hf(kv.first) % _tables.size(); Node* newnode = new Node(kv); newnode->_next = _tables[index]; _tables[index] = newnode; } }; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- (1) 哈希桶的节点以及底层结构
哈希桶的节点是一个单向链表，它得有数据，是一个键值对，还得有 下一个节点的指针。
template<class K,class V> struct HashNode { pair<K, V> _kv; HashNode<K,V>* _next; HashNode(const pair<K, V>& kv) :_kv(kv), _next(nullptr) { } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
哈希桶的底层，是一个数组，数组中存的是节点的指针，当然还得有一个有效数据的个数，它是用于判断是否需要扩容的。
template<class K,class V,class Hashfunc = Hash<K>> class link_hashtable { typedef HashNode<K, V> Node; private: vector<Node*> _tables; size_t _n = 0; public: }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- (2) 哈希桶的查找
查找也简单呢，就是迭代往下查找，如果找到就返回，位置的指针，找不到就返回空。
Node* find(const K& key) { if (_tables.size() == 0) return nullptr; Hashfunc hf; size_t index = hf(key) % _tables.size(); Node* cur = _tables[index]; while (cur) { if (cur->_kv.first == key) return cur; else cur = cur->_next; } return nullptr; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- (3) 哈希桶的插入
bool insert(const pair<K,V>& kv) { Node* ret = find(kv.first); if (ret) { return false; } Hashfunc hf; if (_n == _tables.size()) { size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2; vector<Node*> newTables; newTables.resize(newSize); for (size_t i = 0; i < _tables.size(); ++i) { Node* cur = _tables[i]; while (cur) { Node* next = cur->_next; size_t index = hf(cur->_kv.first) % newTables.size(); // 头插 cur->_next = newTables[index]; newTables[index] = cur; cur = next; } // 将旧桶置空 _tables[i] = nullptr; } _tables.swap(newTables); } size_t index = hf(kv.first) % _tables.size(); Node* newnode = new Node(kv); newnode->_next = _tables[index]; _tables[index] = newnode; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
先考虑插入的数据的key有没有重复，如果重复了那就直接返回。其实就是个头插，中间代码很多是扩容，我们先不考虑扩容，其实 插入的代码就是：
size_t index = hf(kv.first) % _tables.size(); Node* newnode = new Node(kv); newnode->_next = _tables[index]; _tables[index] = newnode;- 1
- 2
- 3
- 4
- 5
扩容的话，和哈希表同理，扩完容之后，哈希桶的位置可能会变化，所以要自己完成重新插入工作，不过扩容的条件不再是 载荷因子 >=0.7，而是 载荷因子等于 1时才扩容。
- (4) 哈希桶的删除
bool erase(const K& key) { Node* ret = find(key); if (ret == nullptr) { return false; } Hashfunc hf; size_t index = hf(key) % _tables.size(); // 前一个节点 Node* pre = nullptr; //桶的第一个节点 Node* cur = _tables[index]; while (cur) { // 桶的下一个节点 Node* next = cur->_next; // 找到要删除的节点 if (cur->_kv.first == key) { // 头删 if (pre == nullptr) { _tables[index] = next; } // 中间删或者尾删 else { pre->_next = next; } delete cur; _n -= 1; return true; } else { // 往桶下面迭代 pre = cur; cur = next; } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
一上来 先检查要删除的数据是否存在，存在就往下走，不存在直接返回。
然后就是 找要删除的数据在那个桶中：
Hashfunc hf; size_t index = hf(key) % _tables.size();- 1
- 2
再就是 在这个桶中 删除，我们需要考虑几件事:
- 桶中是单向链表，删除的话我需要维护链表的关系，所以需要记录删除数据的前一个数据
- 要删除的节点如果是头节点，就不需要维护和前一个数据的关系，因为它就是第一个
- 要删除的节点在中间或者最后，那就需要维护和前一个的关系
3.2.1 扩散列的细节
扩散列是有极端情况的，比如 我开辟的数组大小是 10 ，插入的数据是 10，20，30，40，50，60 …… 10000000000，这些数据都插入到了一个桶里面。
会导致哈希桶变成这样：
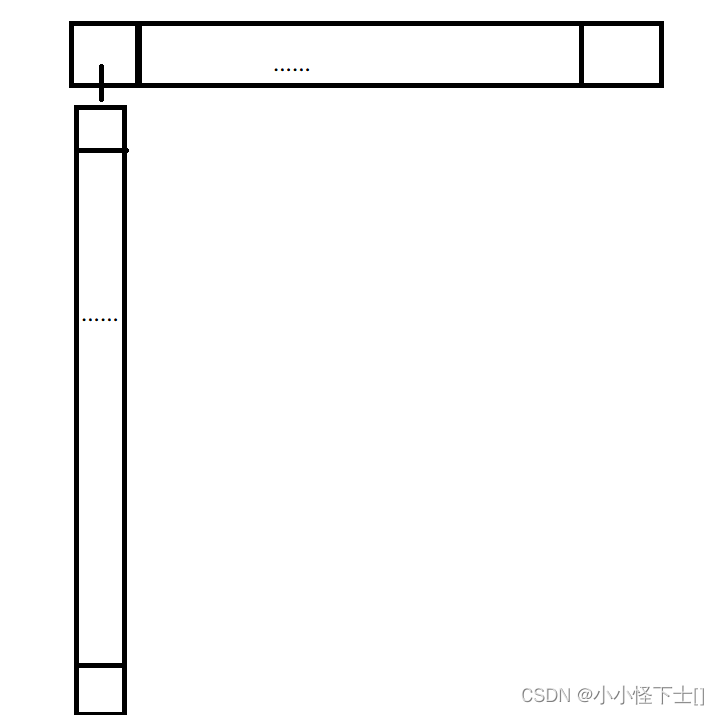
会发现，效率退化了，哈希的查找一般情况是O(1) ，但是这种情况下，退化成O(n)了。所以应该怎么办？大佬其实是给出解决方案的，就是一个桶中的元素超过了某一个
量，那么就会将这个桶中的数据用红黑树组织起来，对于这个量jave和C++还不一样。这就是所谓的
桶中种树。
但是上面的哈希桶，我没有支持这种高级操作，我觉得只要了解这个事情就行了，至于实现，也是可以的，但是对于我们要学习哈希，没太大帮助。
4. 哈希表和哈希桶的比较
哈希桶处理溢出，需要增设链接指针，似乎增加了存储开销。
事实上： 由于哈希表必须保持大量的空闲空间以确保搜索效率，如二次探查法要求装载因子a <= 0.7，而表项所占空间又比指针大的多，所以使用链地址法反而比开地址法节省存储空间。
哈希表处理哈希冲突用的是抢占别的位置，可能会导致数据比较阻塞，也就是每进来一个数据都需要去抢占别人的位置。
哈希桶处理哈希冲突用的是在冲突位置，增加链节点的方法，但是有可能造成，单向链表太长从而影响效率，所以需要将单向链表变为红黑树管理起来。
5. 结尾语
学完哈希，能干什么？说实话哈希很重要，学数据结构，你说你不会哈希，那么就相当于你白学数据结构了，就是这么夸张哈，以后工作也会大量用到哈希的。所以大家加油。在我的下一篇文章中，会利用哈希桶去实现unordered_map和unordered_set，也算是用上了哈希。当然位图呀，布隆过滤器呀，海量处理数据等 都会用到哈希。
-
-
相关阅读:
Vue3实现刷新页面局部内容
VS配置libtorch,torchvision(vision)的一些问题记录
MessagePassing分析与说明
通过LiveGo学习WebSocket
物理层 （physical layer）
闭包-问题大全
xgboost配置GPU
计算机毕业设计springboot+vue基本微信小程序的医疗监督反馈小程序
如何录制视频？有了这款视频录制软件，粉丝多了，转发量也起来了
华为机考入门python3--（36）牛客36-字符串加密
- 原文地址：https://blog.csdn.net/lyzzs222/article/details/127702486
