-
泰勒展开式记忆方法
泰勒认为“仿造一段曲线,要先保证起点相同,再保证在此处导数相同,继续保证在此处的导数的导数相同……”
一、简介
泰勒公式,也称泰勒展开式。是用一个函数在某点的信息,描述其附近取值的公式。如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,泰勒公式可以利用这些导数值来做系数,构建一个多项式近似函数,求得在这一点的邻域中的值。
关于多项式,它本身的运算是有限项的加减法和乘法,因此泰勒思考,能否用多项式函数去近似表达给定的函数。我们期望两个函数在某一点的函数值、一阶导数值、二阶导数值等相等,因为这些值表达了函数图像最基本和最主要的性质,这些性质的逼近可以使得两个函数图像逼近。
余项,即为误差,我们使用多项式函数在某点展开,逼近给定的函数,但是最后肯定会有一点点误差。
二、常见泰勒展开式
1、
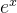
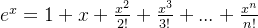
对两边进行求导
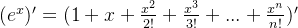
求导得:
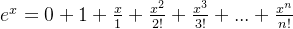
两边都不改变,并且满足
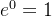
2、
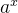
将
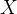 换成
换成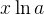 ,带入上面的公式:
,带入上面的公式: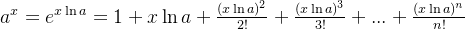
3、
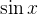
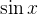 为奇函数,只有奇数项,并且
为奇函数,只有奇数项,并且 ,x的次方数也为奇数项,符号正负交替
,x的次方数也为奇数项,符号正负交替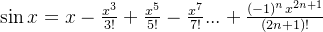
4、
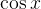
我们可以发现,
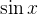 的求导就是
的求导就是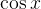
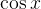 为偶函数,只有偶数项,并且
为偶函数,只有偶数项,并且 ,x的次方也为偶数项,符号正负交替
,x的次方也为偶数项,符号正负交替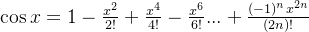
5、
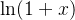
记忆:无阶乘,符号正负交替
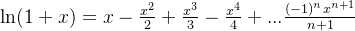
6、

默默地记住它...
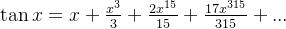
7、
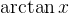
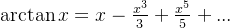
8、

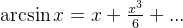
9、最后的汇总

注意:使用泰勒展开式时要注意分子分母同阶
-
相关阅读:
数据化运营05 关注用户留存就够了吗?值得你关注的另外 3 种留存
低代码平台对于开发者来说可以解决哪些问题?
【ARM Coresight Debug 系列 16 -- Linux 断点 BRK 中断使用详细介绍】
mmc命令(do_mmcops函数的源码分析)
平行港口:智慧绿色时代下港口工业智联网新形态与体系结构
yolov6解锁了新姿势
nginx 多层代理 + k8s ingress 后端服务获取客户真实ip 配置
DDoS介绍
深度学习(初识tensorflow2.版本)之三好学生成绩问题(1)
五款最热低代码平台推荐!
- 原文地址:https://blog.csdn.net/weixin_51293984/article/details/127706695