基本排序算法的总结笔记

一直想总结一下最常用的排序算法，自己写一下代码并运行一下记忆更深刻

直接插入排序

1. 说明
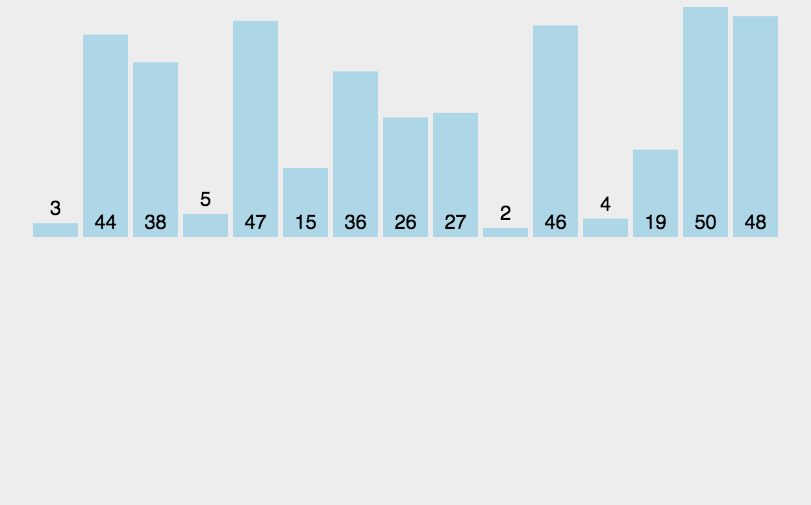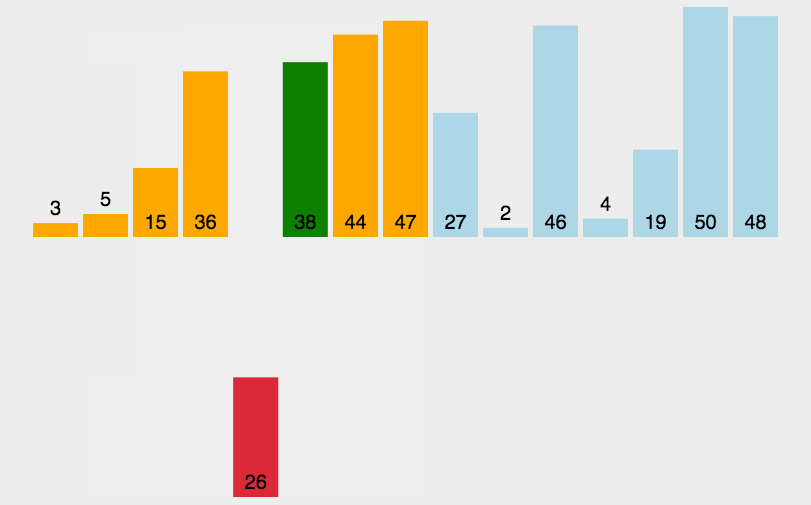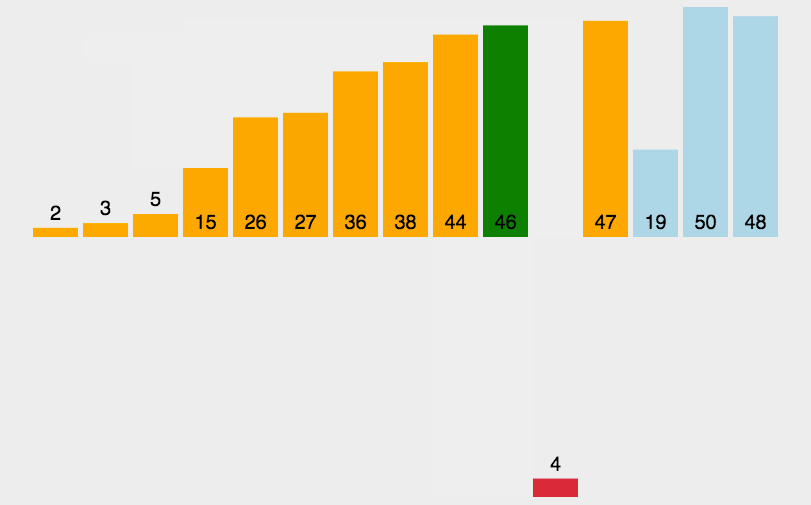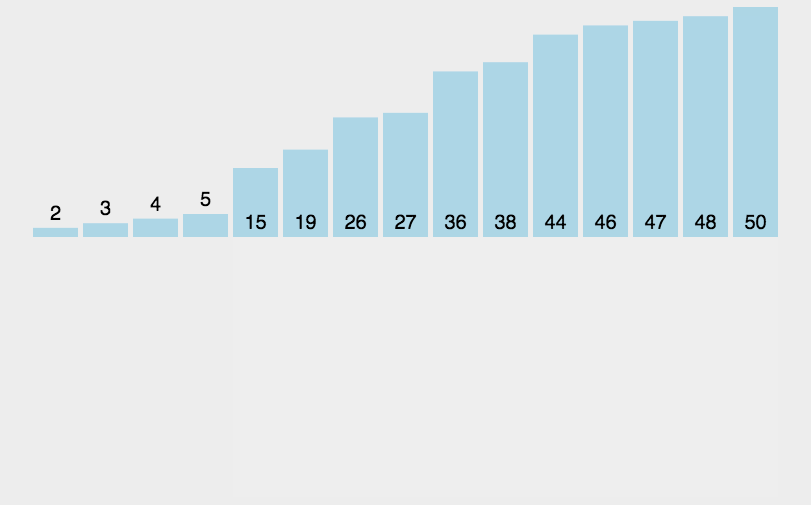
   每步将一个待排序的记录，按其排序码大小，插到前面已经排序的文件中的适当位置，直到全部插入完为止。
   原理：从待排序的n个记录中的第二个记录开始，依次与前面的记录比较并寻找插入的位置，每次外循环结束后，将当前的数插入到合适的位置。
   

2. 平均时间复杂度
   平均复杂度 O(n²)
   最好情况 O(n)
   最坏情况 O(n²)
   空间复杂度O(1);
   稳定性 稳定

3. 适用场景
   插入排序由于O( n2 )的复杂度，在数组较大的时候不适用。它适用于简单数据排序。

4. 代码

/**
 * 简单插入排序
 */
public class InsertSort {

    public static void insertSort(int[] arr){
        int temp;
        int length = arr.length;
        for(int i=1;i<length;i++){
            int j = i-1;
            temp = arr[i];
            while(j>=0 && arr[j] > temp){
                arr[j+1] = arr[j];
                j--;
            }
            if(j != i-1){
                arr[j+1] = temp;
            }
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

希尔排序

1. 说明
   在希尔排序出现之前，计算机界普遍存在“排序算法不可能突破O(n2)”的观点。希尔排序是第一个突破O(n2)的排序算法，它是简单插入排序的改进版。
   希尔排序是对直接插入排序的改进算法。希尔排序是通过分组+插入，先分组再插入。

3. 平均时间复杂度
   平均复杂度 O(nlogn)
   最好情况 O(n log²n)
   最坏情况 O(n log²n)
   空间复杂度O(1);
   稳定性 不稳定

4. 适用场景
   Shell排序虽然快，但是毕竟是插入排序，其数量级并没有后起之秀–快速排序O(n㏒n)快。在大量数据面前，Shell排序不是一个好的算法。但是，中小型规模的数据完全可以使用它。

5. 代码

/**
 * 快速排序
 */
public class QuickSort {

    public static void quickSort(int[] arr,int start,int end){
        if(start>end) return;
        int left = start;
        int right = end;
        int base = arr[start];
        while(left != right){
            while(left<right && arr[right]>=base){right--;}
            while(left<right && arr[left] <= base){left++;}
            if(left<right){
                swap(arr,left,right);
            }
        }
        swap(arr,start,left);
        quickSort(arr,start,left-1);
        quickSort(arr,left+1,end);
    }

    public static void swap(int[] arr,int left,int right){
        int temp = arr[left];
        arr[left] = arr[right];
        arr[right] = temp;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

冒泡排序

1. 说明
   交换排序的基本方法是：两两比较待排序记录的排序码，交换不满足顺序要求的偶对，直到全部满足位置。常见的冒泡排序和快速排序就属于交换类排序。
   算法思想： 从数组中第一个数开始，依次遍历数组中的每一个数，通过相邻比较交换，每一轮循环下来找出剩余未排序数的中的最大数并”冒泡”至数列的顶端。

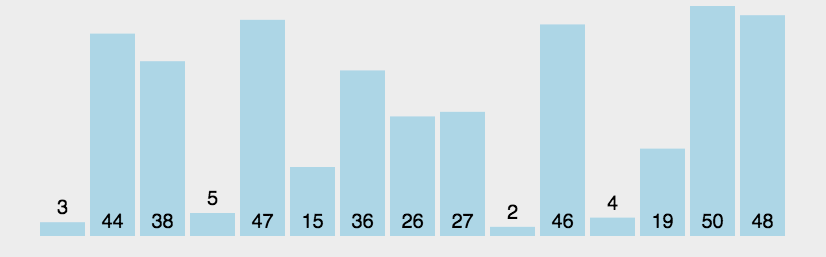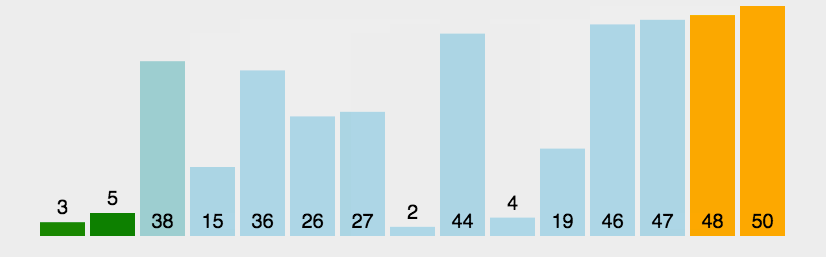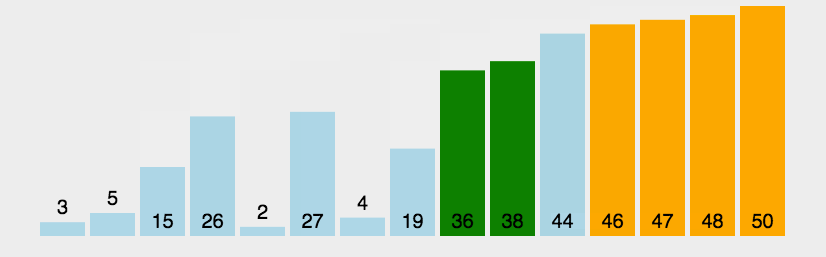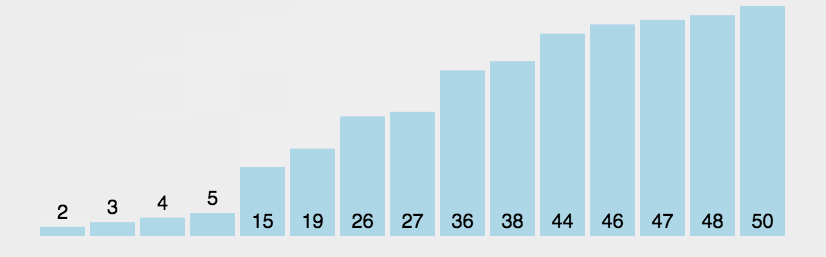
2. 平均时间复杂度：O(n2)
   平均复杂度 O(n²)
   最好情况 O(n)
   最坏情况 O(n²)
   空间复杂度O(1);
   稳定性 稳定

3. 适用场景
   它适用于简单数据排序。

4. 代码

/**
 * 冒泡排序
 */
public class BubleSort {

    public static void bubbleSort(int[] array){
        int length = array.length;
        for(int i=0;i<=length-1;i++){
            boolean swap = Boolean.FALSE;
            for(int j=0;j<length-1-i;j++){
                if(array[j]>array[j+1]){
                    swap(array,j,j+1);
                    swap = Boolean.TRUE;
                }
            }
            if(!swap){
                //已经没有交换了，跳出循环
                break;
            }
        }
    }

    /**
     * 交换函数
     * @param array
     * @param left
     * @param right
     */
    public static void swap(int[] array,int left,int right){
        // 算法一
        int temp = array[left];
        array[left] = array[right];
        array[right] = temp;

        // 算法二
//        array[left] = array[left] +array[right];
//        array[right] = array[left] - array[right];
//        array[left] = array[left]  - array[right];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

快速排序

1. 说明
   快速排序是一个既高效又不浪费空间的一种排序算法，面试问排序的基本题。
   快速排序是对冒泡排序的改进算法，快速排序采用的思想是分治思想。
   冒泡排序是在相邻的两个记录进行比较和交换，每次交换只能上移或下移一个位置，导致总的比较与移动次数较多。快速排序简单来说就是定义一个标准，大于标准的放一边，小于标准的方另一边，再递归。

2. 平均时间复杂度
   平均复杂度 O(nlogn)
   最好情况 O(nlogn)
   最坏情况 O(n²)
   空间复杂度O(logn);
   稳定性 不稳定

3. 适用场景
   快速排序在大多数情况下都是适用的，尤其在数据量大的时候性能优越性更加明显。但是在必要的时候，需要考虑下优化以提高其在最坏情况下的性能。

4. 代码

/**
 * 快速排序
 */
public class QuickSort {

    public static void quickSort(int[] arr,int start,int end){
        if(start>end) return;
        int left = start;
        int right = end;
        int base = arr[start];
        while(left != right){
            while(left<right && arr[right]>=base){right--;}
            while(left<right && arr[left] <= base){left++;}
            if(left<right){
                swap(arr,left,right);
            }
        }
        swap(arr,start,left);
        quickSort(arr,start,left-1);
        quickSort(arr,left+1,end);
    }

    public static void swap(int[] arr,int left,int right){
        int temp = arr[left];
        arr[left] = arr[right];
        arr[right] = temp;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

简单选择排序

1. 说明
   选择类排序的基本方法是：每步从待排序记录中选出排序码最小的记录，顺序放在已排序的记录序列的后面，直到全部排完。
   

2. 时间复杂度
   平均复杂度 O(n²)
   最好情况 O(n²)
   最坏情况 O(n²)
   空间复杂度O(1);
   稳定性 不稳定

3. 适用场景
   选择排序实现也比较简单，由于固有的O(n2)复杂度，选择排序在海量数据面前显得力不从心。因此，它适用于简单数据排序。

4. 代码

/**
 * 简单选择排序
 */
public class SelectionSort {

    public static void selectionSort(int[] arr){
        int length = arr.length;
        int minIndex;
        for(int i=0;i<length -1;i++){
            minIndex = i;
            for(int j= i+1;j<=length-1;j++){
                if(arr[j] < arr[minIndex]){
                    minIndex = j;
                }
            }
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

堆排序

1. 说明

2. 平均时间复杂度
   平均复杂度 O(nlongn)
   最好情况 O(nlogn)
   最坏情况 O(nlogn)
   空间复杂度O(1);
   稳定性 不稳定

3. 适用场景
   堆排序在建立堆和调整堆的过程中会产生比较大的开销，在元素少的时候并不适用。但是，在元素比较多的情况下，还是不错的一个选择。尤其是在解决诸如“前n大的数”一类问题时，几乎是首选算法。

4. 代码

参考：
[算法总结] 十大排序算法
十种排序算法