Cauchy distribution

0、背景

柯西分布，也称为柯西-洛伦兹分布或洛伦兹分布，是描述共振行为的连续分布。它还描述了以随机角度倾斜的线段切割 x 轴的水平距离分布。如图：我们从原点引出射线，相邻射线角度相等，这些射线与平行于x轴的直线S有交点，这些交点在S线上的密度是不同的，显然，在90°的附近密度最大。

 1、公式推导

 根据上图，可以得出以下公式推导：

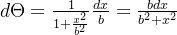
dθπ=1πbdxb2+x2dθπ=1πbdxb2+x2

对上式分别左右两端进行积分可得：

∫π/2−π/2dθπ=1∫π/2−π/2dθπ=1

∫∞−∞1πbdxb2+x2=1π[tan−1(xb)]∞−∞=1π[12π−(−12π)]=1

可以看出从左边Θ∈[−π2,π2]到右边x∈[−∞,∞]，虽然自变量的范围发生了改变，但是左右两边等式的值并没发生变化，都是等于1。由此推出了今天的主角，柯西分布。

柯西分布的概率密度函数为：  

P(x)=1πb(x−m)2+b2

P(x)在x=m时候达到最大值。 m是定义峰值位置的位置参数，b是尺度参数。

柯西分布的累计分布函数为：

D(x)=∫x−∞1πbdxb2+(x−m)2=1π[arctan(x−mb)]x−∞=12+1πarctan(x−mb)

D(x)最大值为1，对应的x为正无穷。如果m=0，b=1，那么就得到了标准柯西分布。

标准柯西分布的概率密度函数为：

P(x)=1π×1x2+1

标准柯西分布的累计分布函数为：

D(x)=12+1πarctan(x)

2、公式的代码实现

function y = Cauchy_PDF(x,m,b)
y = (1/pi) * (b ./ ((x - m).^2 + b.^2));
end

标准柯西分布P(x)画出对应的直角坐标系图：

function y = Cauchy_CDF(x,m,b)
y = 0.5 + (1 / pi) .* atan((x - m)./b);
end

 标准柯西分布D(x)画出对应的直角坐标系图：

 现在画出标准正态分布的概率密度函数和累计分布函数：

 

 发现：柯西分布的取值范围非常广，很大的值也有一定概率取到。相比较而言高斯分布在[-3,3]之外取值的可能性非常之低。

3、获取柯西分布随机数

生成柯西随机数的步骤：

• 计算得到Cauchy分布累计分布函数(CDF)的反函数；
• 使用rand()函数生成(0,1)区间上均匀分布的初始随机数u；
• 将初始随机数代入CDF的反函数即可得到我们需要的Cauchy随机数：

Cauchy分布累计分布函数(CDF)的反函数：

x=m−btan(πu)

function y = Cauchy_rand(m,b)
u = rand();
y = m - (b ./ tan(pi .* u));
end

3.1 利用MATLAB自带工具箱

当ν等于1时，t Location-Scale Distribution就变为柯西分布了。当σ=1，μ=0时，t Location-Scale Distribution就变为标准柯西分布了。

clc;clearvars;clear;
% 转化为标准柯西分布
pd = makedist('tLocationScale','mu',0,'sigma',1,'nu',1);
% 画出标准柯西分布
x = -20:1:20;
y = pdf(pd,x);
plot(x,y,'LineWidth',2)
r1 = random(pd,10,1);%生成10个柯西随机数
r2 = random(pd,5,5);%生成一个柯西随机生成矩阵
disp(r1);
disp(r2);

 

如有错误，还望批评改正。