【问题思考总结】为什么跳跃间断点变上限积分连续但是不可导？【直观理解 几何方法】

问题

在搜索变上限积分相关知识的时候，对于间断点对变上限积分的影响不是很了解，找了很多资料都是严谨地证明，对于我这种考研只想把公式记下来，然后有一定理解的要求显然不符合，因此，在这里总结一种几何的理解。

理解

先看结论：

1.当函数连续时，变上限积分一定可导。

举例：

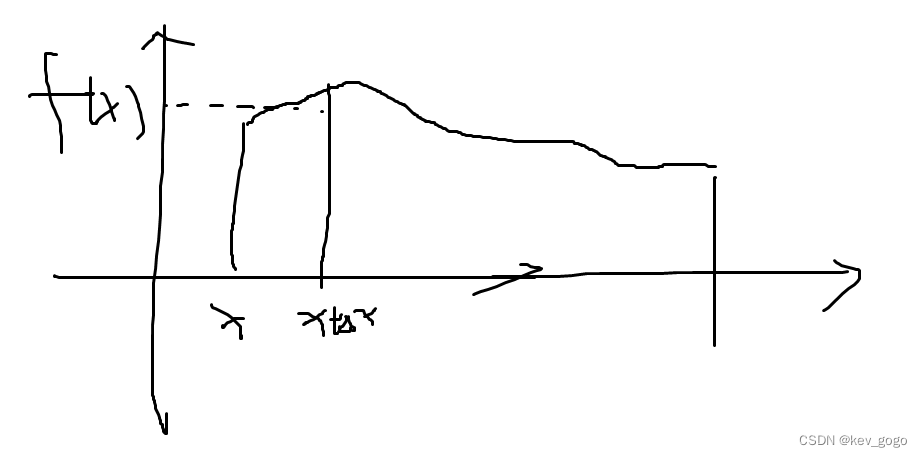
我们可以想象一下，讨论变限积分的可导性，其实就是讨论变限积分的变化率，积分是面积，那么变化率是什么呢？想象一个极小的区间【x，x+Δx】，变化量就是Δx*fx（因为是极小的区间，因此以直代曲，变化量是一个矩形）

那么变化率就是矩形的面积除以Δx，也就是fx。那么讨论可导性，导数是fx，fx存在则导数存在，那么fx连续，自然导数处处存在。

2.函数有可去间断点，变上限积分可导

举例：

这个地方是一个难点，包括公式证明的时候，对于这一个没有定义的点也是比较麻烦（采取了用极限值代替函数值的方法，但是本质上实际上还是用了几何意义，因此我们这里直接用几何意义进行说明）

之前我们提到，函数值存在就是导数存在。那么在这个区间上，有函数值不存在的点我们应该怎么考虑呢？

在之前的文章中提到过：一个极限是一个无穷逼近的过程，是一个函数，限定了他可以无限地接近一点。

【问题思考总结】一个大于0的数乘以无穷大一定是无穷大吗？【关于定点和动点，数和函数，定区间和变区间的辨析】

但是实际上，极限即使再小，他也是和一个邻域相关，因此本质上是一个区间。
在这里，我们的间断点实际上是一个点，那么它对应的面积是一条线的面积也就是0（Δx乘以函数值是有面积的），因此，这个间断点对面积的影响可以忽略不计，因此，对面积的变化率即积分的导数也就是没有影响。间断点没问题，整个函数自然也没问题了，等同于情况1。（好抽象）

3. 函数有跳跃间断点，变上限积分连续但是不可导

举例：

在这种情况下，刚才说的，线不影响面积，也不影响变化率，那么这个不是必然可导吗？
实际上不是的，因为之前这种说法成立是建立在fx除间断点，其他地方都是连续变化的。即在可去间断点的左右两侧**，左极限等于右极限。而这里显然不成立**。

因为我们这个变化率是用邻域定义的，考虑fx的左右极限，易证左极限不等于右极限（左边的变化率不等于右边的变化率），因此，面积在该点的变化率不存在，即变限积分在该点的导数不存在（这种方法也可以说明变限积分在可去间断点上的导数存在，但是这种方法说明不存在要更好一些，因为在可去间断点中涉及到补充定义的问题）

而又因为面积是逐渐变化的，因此，在面积的图象上是连续的，只不过是有尖点。
举例：

或者简洁一点记忆：函数越积分性质越好，因此之前有间断点的，积分完一定连续，之前连续的，积分完一定可导。

总结

变上限积分

1. fx连续，变上限积分可导
2. fx可去，变上限积分可导
3. fx跳跃，变上限积分连续但是不可导

相关知识（个人总结）

可积性（定积分）

必要条件：可积则区间上一定有界。
充分条件：

1. 连续必可积
2. 有界且只有有限个间断点（第一类或者震荡）

原函数的存在性

1. 连续一定有原函数
2. 有第一类间断点一定没有原函数
3. 有第二类间断点可能有原函数

有兴趣的小伙伴可以查一下证明。
以上均为思考和总结，如果有错误的地方请帮忙指正，定会致谢，欢迎博友一起讨论。