数据结构与算法----详解二叉树的遍历(迭代、递归)

• ❤️ 作者简介：大家好我是小鱼干儿♛是一个热爱编程、热爱算法的大三学生，蓝桥杯国赛二等奖获得者
• 🐟 个人主页 ：https://blog.csdn.net/qq_52007481
• ⭐ 个人社区：【小鱼干爱编程】
• 🔥 算法专栏：算法竞赛进阶指南
• 💯 刷题网站：虽然市面上有很多的刷题网站，但是里面的题又多又杂，不适合系统性的提高算法能力，如何挑选一个适合自己的刷题网站呢，这里推荐一款我常用的刷题网站 👉牛客网

---

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分。--------百度百科

二叉树的遍历是使用二叉树的最基础的操作，常见的几种遍历方式有，前序遍历，中序遍历，后续遍历，层次遍历，这里所说的前、中、后是表示父节点被访问的次序，层次节点是表示一层一层，从左往右访问节点

实现二叉树的类

因为这里是讲解的二叉树的几种遍历形式，二叉树添加的数据的部分就不再写了,
结果测试我们就去刷题网站测试：牛客网

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
1
2
3
4
5

每种遍历都有两种方式递归、迭代，因为递归不仅容易出现超过最大递归深度，而且非常浪费计算机资源，因此在实际使用过程中我们应该尽量的避免递归,在大多数情况下递归都有对应的迭代版本。

在实现二叉树的迭代遍历的过程中，使用了栈的思想，我们会用一个栈来存储节点的位置

前序遍历

前序遍历：父节点 > 左节点 > 右节点

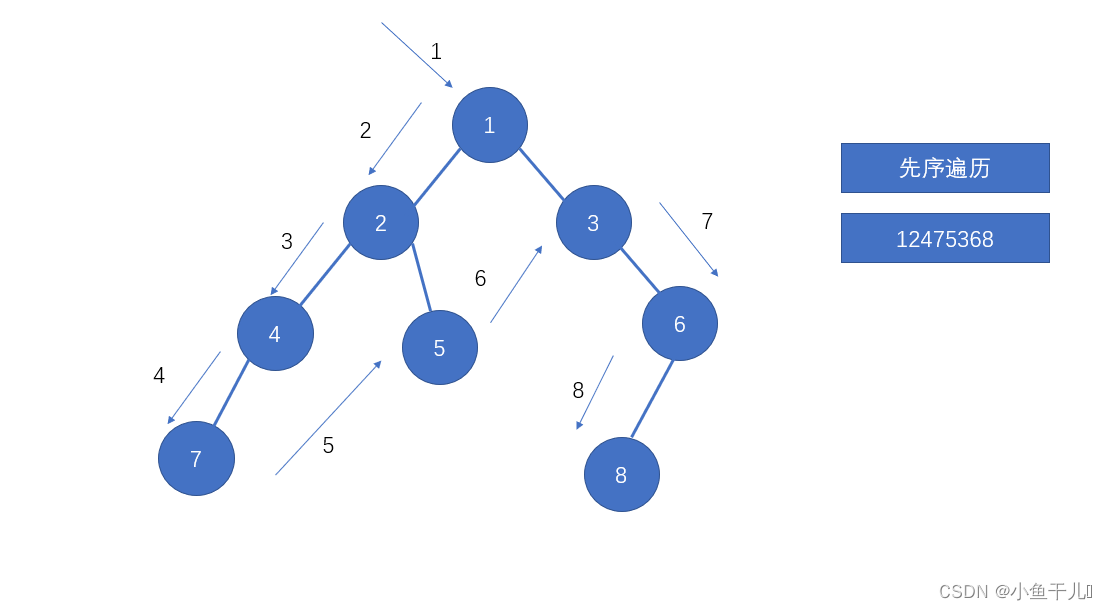
• 递归方式

arr = []
def preOrder(root):
    if root==None:    # 函数停止的条件，
        return 
    arr.append(root.val)   # 先存放父节点的元素
    preOrder(root.left)    # 将左节点当作一个树，继续执行 
    
    preOrder(root.right)   # 将右节点当作一个树，继续执行 
1
2
3
4
5
6
7
8

• 迭代方式

栈的作用就是存储还未被遍历节点的指针，等后面使用的时候在取出
工作流程：

• 3进栈，2进栈、输出1的值，2出栈
• 5进栈，4进栈、输出2的值，4出栈
• 7进栈，输出4的值，7出栈
• 输出7的值，3出栈
• 6进栈，输出3的值，6出栈
• 8进栈，输出6的值，8出栈
• 输出8的值

stack = []   # 栈，用来存储节点的指针
while root:  # 当二叉树存在时执行循环
    if root.right !=None:  # 因为是先序遍历，所有右边的节点要先进栈
        stack.append(root.right)
    if root.left!=None:
        stack.append(root.left)
    print(root.val)       #  每循环一个节点就输出一个值，可以根据需要调整
    if len(stack) == 0:
        break
    else:
        root = stack.pop()   # 弹出栈顶的元素 
1
2
3
4
5
6
7
8
9
10
11

中序遍历

中序遍历：中节点 > 父节点 > 右节点

• 递归方式

arr = []
def medOrder(root):
    if root==None:
        return 
    medOrder(root.left)     # 先找到最左叶子节点，
    arr.append(root.val)    # 
    medOrder(root.right)
1
2
3
4
5
6
7

• 迭代方式
  先找到最左节点，从最左节点开始遍历二叉树

工作流程：

• 1进栈
• 2进栈
• 4进栈
• 7进栈
• 7出栈 输出7的值
• 4出栈 输出4的值
• 2出栈，输出2的值，
• 5进栈
• 5出栈，输出5的值
• 1出栈，输出1的值
• 3进栈
• 3出栈，输出3的值
• 6进栈
• 8进栈，输出8的值
• 6出栈，输出6的值

stack = []
while True:
    if root:
        stack.append(root)  # 将节点存入栈中
        root = root.left
    elif len(stack)>0:
        root = stack.pop()  # 取出栈顶的元素，第一次取到的是最左节点，
        print(root.val)
        root = root.right   
    else:
        break
1
2
3
4
5
6
7
8
9
10
11

后序遍历

后序遍历：左节点 > 右节点 > 父节点

• 递归方式

arr = []
def postOrder(root):
    if root==None:
        return 
    postOrder(root.left)
    postOrder(root.right)
    arr.append(root.val)
1
2
3
4
5
6
7

• 迭代方式
  因为父节点在左右节点的之间，所以用迭代的方式实现后续遍历，比较困难，需要一个额外的数组用来存放左右两边都遍历过的父节点。

• 1进栈
• 2进栈
• 4进栈
• 7进栈
• 7出栈，输出7的值
• 4出栈，输出4的值
• 2出栈，左节点还未被遍历，2重新进栈
• 5进栈
• 5出栈， 输出5的值
• 2出栈，输出2的值
• 1出栈，左节点还未被遍历，1重新进栈
• 3进栈
• 6进栈
• 8进栈
• 8出栈，输出8的值
• 6出栈，输出6的值
• 3出栈，输出3的值
• 1出栈，输出1的值

stack = []  # 栈
lst = []  # 存放左右两边都被遍历过父节点
while True:
    if root:
        stack.append(root)   # 将节点入栈
        root = root.left     # 将左节点当作新的二叉树
    elif len(stack)>0:
        root = stack.pop()    # 弹出栈顶的元素
        if root.right:   # 查看该节点是否有右节点，如果有判断是否被遍历过
            if root in lst:  # 该节点的左右两边都被遍历
                lst.remove(root)  # 从该数组中删除，(不删除也可以，删除会减少内存空间)
                print(root.val)   # 输出该值
                root = None       # 因为都被访问过了，就类似一个空树
            else:   # 该节点的右节点还未被遍历
                stack.append(root)  # 重新将该节点入栈
                lst.append(root)    # 其实此时可能并没有遍历，但是因为栈的特性，我们可以知道遍历右节点一定早于父节点所以可以添加到左右两边都被遍历的数组中
                root = root.right   # 将右节点当作一个新的二叉树，继续循环               
        else:
            print(root.val)
            root = None      # 当没有右节点，则代表树为空
    else:
        break
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

层次遍历

层次遍历只有迭代版本
层次遍历使用的就不是栈， 使用的是队列(先进先出)

算法执行的流程

• 1入队
• 1出队，输出1的值，2入队，3入队
• 2出队，输出2的值，4入队，5入队
• 3出队，输出3的值，6入队
• 4出队，输出4的值，7入队
• 5出队，输出5的值
• 6出队，输出6的值，8
• 7出队，输出7的值
• 8出队，输出8的值

queue = []
if root == None:
    return []
queue.append(root)
while len(queue)>0:
    root = queue.pop(0)
    print(root.val)
    if root.left != None:
        queue.append(root.left)
    if root.right != None:
        queue.append(root.right)
1
2
3
4
5
6
7
8
9
10
11

练习题：

👉直达牛客，快人一步

题解1，使用递归解题

class Solution:
    def threeOrders(self , root: TreeNode) -> List[List[int]]:
        # write code here
        # 先序遍历
        arr = [[],[],[]]
        def preOrder(root):
            if root==None:
                return
            arr[0].append(root.val)
            preOrder(root.left)
            preOrder(root.right)
        preOrder(root)
        def medOrder(root):
            if root==None:
                return
            medOrder(root.left)
            arr[1].append(root.val)
            medOrder(root.right)
        medOrder(root)
        def postOrder(root):
            if root==None:
                return
            postOrder(root.left)
            postOrder(root.right)
            arr[2].append(root.val)
        postOrder(root)
        return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

题解2，简化递归，
从第一个我们能够发现，前序后续的算法非常相似，只是顺序有区别，我们其实可以将这些同时放在一个函数里面。

class Solution:
    def threeOrders(self , root: TreeNode) -> List[List[int]]:
        arr = [[],[],[]]
        def Order(root):
            if root==None:
                return
            arr[0].append(root.val)
            Order(root.left)
            arr[1].append(root.val)
            Order(root.right)
            arr[2].append(root.val)
        Order(root)
        return arr
1
2
3
4
5
6
7
8
9
10
11
12
13

题解3 使用迭代
使用迭代的，虽然看着代码非常复杂，但是随着数据量的增多，效率会比迭代的越来越强。

class Solution:
    def threeOrders(self , root: TreeNode) -> List[List[int]]:
        # write code here
        # 先序遍历
        base = root
        arr = [[],[],[]]
        stack = []
        while root:
            if root.right !=None:
                stack.append(root.right)
            if root.left!=None:
                stack.append(root.left)
            arr[0].append(root.val)
            if len(stack) == 0:
                break
            else:
                root = stack.pop(len(stack)-1)
                
        root = base
        stack = []
        while True:
            if root:
                stack.append(root)
                root = root.left
     
            elif len(stack)>0:
                root = stack.pop()
                arr[1].append(root.val)
                 
                root = root.right
            else:
                break
 
        root = base
        stack = []
        lst = []
        while True:
            if root:
                stack.append(root)
                root = root.left
            elif len(stack)>0:
                root = stack.pop()
                if root.right:
                    if root in lst:
                        lst.remove(root)
                        arr[2].append(root.val)
                        root = None
                    else:
                        stack.append(root)
                        lst.append(root)
                        root = root.right
                         
                else:
                    # 取值
                    arr[2].append(root.val)
                    root = None
            else:
                break
        return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

总结

二叉树遍历的遍历，递归的函数比较容易写，但是太浪费计算机的资源，所以要改写为迭代的方式实现。我们在使用迭代实现的时候，应用了栈的思想，层次遍历使用了队列的思想

补充：因为这篇文章是需要有一定的基础的，大家如果对栈和队列不太明白的可以看我这篇文章数据结构与算法----栈和队列(Stack & Queue）
如果文章有哪些问题也欢迎大家大家指正