BRIAN中的STDP示例

STDP简单来说就是根据脉冲到达前后神经元的时间差来更新连接这两个神经元之间的突触权重。
普通更新是这样的：

从公式可以直观看出来：权重更新的前提是连接当前突触的前后两个神经元都要发射脉冲，也就是都要被激活，不然的话，整个网络是不存在更新的。
官方文档最后给了一个例子，但是没有说明，这里就简单补充说明一下，最后再验证一下多个脉冲发射的情况。

首先是例子的解释：

start_scope()

taupre = taupost = 20*ms
Apre = 0.01
Apost = -Apre*taupre/taupost*1.05
tmax = 50*ms
N = 100

# Presynaptic neurons G spike at times from 0 to tmax
# Postsynaptic neurons G spike at times from tmax to 0
# So difference in spike times will vary from -tmax to +tmax
G = NeuronGroup(N, 'tspike:second', threshold='t>tspike', refractory=100*ms)
H = NeuronGroup(N, 'tspike:second', threshold='t>tspike', refractory=100*ms)
G.tspike = 'i*tmax/(N-1)'
H.tspike = '(N-1-i)*tmax/(N-1)'

S = Synapses(G, H,
             '''
             w : 1
             dapre/dt = -apre/taupre : 1 (event-driven)
             dapost/dt = -apost/taupost : 1 (event-driven)
             ''',
             on_pre='''
             apre += Apre
             w = w+apost
             ''',
             on_post='''
             apost += Apost
             w = w+apre
             ''')
S.connect(j='i')

run(tmax+1*ms)

plot((H.tspike-G.tspike)/ms, S.w)
xlabel(r'$\Delta t$ (ms)')
ylabel(r'$\Delta w$')
axhline(0, ls='-', c='k');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

这个例子给的比较直观，只要按照官方的说明文档看过前面的，基本能够理解：
首先，定义了一些相关的基本参数，随后定义了两组神经元，每组神经元的个数是100.
根据连接方式，可以看出来，前后两组神经元连接是一对一的。可以画图看看。

def visualise_connectivity(S):
    Ns = len(S.source)
    Nt = len(S.target)
    figure(figsize=(10, 4))
    subplot(121)
    plot(zeros(Ns), arange(Ns), 'ok', ms=10)
    plot(ones(Nt), arange(Nt), 'ok', ms=10)
    for i, j in zip(S.i, S.j):
        plot([0, 1], [i, j], '-k')
    xticks([0, 1], ['Source', 'Target'])
    ylabel('Neuron index')
    xlim(-0.1, 1.1)
    ylim(-1, max(Ns, Nt))
    subplot(122)
    plot(S.i, S.j, 'ok')
    xlim(-1, Ns)
    ylim(-1, Nt)
    xlabel('Source neuron index')
    ylabel('Target neuron index')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

visualise_connectivity(S)
1

运行上面可视化之后可以看到：

显示有点密集，到那时意思是没有问题的，就是一对一的连接。
这里将每个神经元的发射方式定义为超过固定的时间，也就是说第一个神经元超过0就发放，后面的时间根据表达式G.tspike = 'i*tmax/(N-1)'来计算。
后面神经元发放时间刚好是相反的。
这样一来，按照规定的时间运行，就可以根据定义的规则对权重进行更新，就有了最后的可视化结果：

横坐标是时间差，纵坐标是更新的权重。【正是因为有了每个神经元只发放一次的约束，所以采能这样直接画出来，不然的话，如果发放多次，需要用多次更新的累加和来更新权重】
如果将运行时间缩短，也就是修改代码run(tmax/2+3*ms)
那么出来的图像就会发生变化：

可以看到，只有中间时间差更新了权重，而其他突触还是初始值0.
为什么是中间的呢？可以这么直观理解一下：
第一组发射的时间假设是0，2，4，6，8
第二组发射的时间就是8，6，4，2，0
如果我们只运行四个步骤，第一组0和第二组0代号的神经元就不会更新。严格来说，当前第四步也不会更新，因为神经元的发射条件是大于当前时间。这也就是为什么给的官方示例代码运行的时候多加了1ms

run(tmax+1*ms)
1

如果单个神经元发射多次呢？官方没有给代码，我这里给一个根据官方代码改写的示例:

start_scope()

taupre = taupost = 20*ms
Apre = 0.01
Apost = -Apre*taupre/taupost*1.05
tmax = 50*ms
N = 1

# Presynaptic neurons G spike at times from 0 to tmax
# Postsynaptic neurons G spike at times from tmax to 0
# So difference in spike times will vary from -tmax to +tmax
indices_g = [0,0,0,1]
times_g = [0,10,40,40]*ms
G = SpikeGeneratorGroup(2, indices_g, times_g)
indices_h = [0]
times_h = [30]*ms
H = SpikeGeneratorGroup(1, indices_h, times_h)
# G.tspike = [0,40]*ms
# H.tspike = [30]*ms

S = Synapses(G, H,
             '''
             w : 1
             dapre/dt = -apre/taupre : 1 (event-driven)
             dapost/dt = -apost/taupost : 1 (event-driven)
             ''',
             on_pre='''
             apre += Apre
             w = w+apost
             ''',
             on_post='''
             apost += Apost
             w = w+apre
             ''')
S.connect()

g_mon = SpikeMonitor(G)

run(tmax+1*ms)

plot(S.w)
ylabel(r'$\Delta w$')
axhline(0, ls='-', c='k');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

为了让同一个神经元在不同的时刻产生脉冲，这里修改原始代码，使用了SpikeGeneratorGroup，通过参数indices_g = [0,0,0,1] times_g = [0,10,40,40]*ms
让代号为0的神经元在0ms,10ms,40ms，发射三次脉冲。神经元的连接很简单，如下图所示

权重更新会是什么结果呢？

因为只有两个突触，权重看图不如直接看数值：

可以看到，两个权重都变成了负数，因为权重的初始值是0，第二组的单个神经元发射时间是30ms，而第一组中的两个神经在40ms的时候都发射过脉冲，根据赫布规则，也就是STDP，权重应该减弱，但是显然，第一个权重，要大些，这是因为除了40ms的脉冲之外，第一个权重对应的神经元在30ms之前也发射过脉冲，具体的计算过程如下图所示：

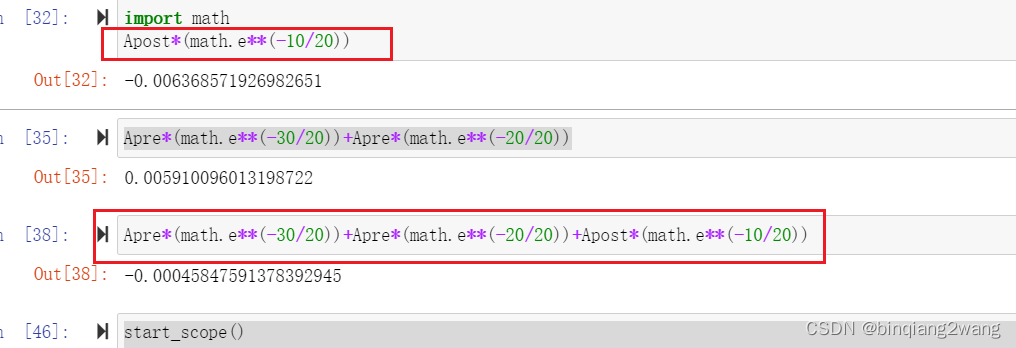
分别是两个权重的来源，就是套最开始的公式。
之前对于STDP都是感性的认知，这是第一次用BRIAN来从数值角度计算，所以记录一下，以备未来肯定 会忘记的自己查看。