-
R语言方差分析总结
本文首发于公众号:医学和生信笔记,完美观看体验请至公众号查看本文。
医学和生信笔记,专注R语言在临床医学中的使用,R语言数据分析和可视化。
介绍各种类型方差分析的R语言实现方法,目录如下:
文章目录
这篇文章涵盖了孙振球,徐勇勇《医学统计学》第4版中关于方差分析的章节,包括:多样本均数比较的方差分析/多因素实验资料的方差分析/重复测量设计资料的方差分析/协方差分析。
本书电子版及配套数据已放在QQ群,需要的加群下载即可。

多样本均数比较的方差分析
完全随机设计资料的方差分析
使用课本例4-2的数据。
首先是构造数据,本次数据自己从书上摘录。。
trt<-c(rep("group1",30),rep("group2",30),rep("group3",30),rep("group4",30)) weight<-c(3.53,4.59,4.34,2.66,3.59,3.13,3.30,4.04,3.53,3.56,3.85,4.07,1.37, 3.93,2.33,2.98,4.00,3.55,2.64,2.56,3.50,3.25,2.96,4.30,3.52,3.93, 4.19,2.96,4.16,2.59,2.42,3.36,4.32,2.34,2.68,2.95,2.36,2.56,2.52, 2.27,2.98,3.72,2.65,2.22,2.90,1.98,2.63,2.86,2.93,2.17,2.72,1.56, 3.11,1.81,1.77,2.80,3.57,2.97,4.02,2.31,2.86,2.28,2.39,2.28,2.48, 2.28,3.48,2.42,2.41,2.66,3.29,2.70,2.66,3.68,2.65,2.66,2.32,2.61, 3.64,2.58,3.65,3.21,2.23,2.32,2.68,3.04,2.81,3.02,1.97,1.68,0.89, 1.06,1.08,1.27,1.63,1.89,1.31,2.51,1.88,1.41,3.19,1.92,0.94,2.11, 2.81,1.98,1.74,2.16,3.37,2.97,1.69,1.19,2.17,2.28,1.72,2.47,1.02, 2.52,2.10,3.71) data1<-data.frame(trt,weight) head(data1)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
## trt weight ## 1 group1 3.53 ## 2 group1 4.59 ## 3 group1 4.34 ## 4 group1 2.66 ## 5 group1 3.59 ## 6 group1 3.13- 1
- 2
- 3
- 4
- 5
- 6
- 7
数据一共两列,第一列是分组(一共四组),第二列是低密度脂蛋白测量值:

先简单看下数据分布
boxplot(weight ~ trt, data = data1)- 1

进行完全随机设计资料的方差分析(one-way anova):
fit <- aov(weight ~ trt, data = data1) summary(fit)- 1
- 2
## Df Sum Sq Mean Sq F value Pr(>F) ## trt 3 32.16 10.719 24.88 1.67e-12 *** ## Residuals 116 49.97 0.431 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
结果显示组间自由度为3,组内自由度为116,组间离均差平方和为32.16,组内离均差平方和为49.97,组间均方为10.719,组内均方为0.431,F值=24.88,p=1.67e-12,和课本一致。
再简单介绍一下可视化的平均数和可信区间的方法:
library(gplots)- 1
## ## Attaching package: 'gplots'- 1
- 2
## The following object is masked from 'package:stats': ## ## lowess- 1
- 2
- 3
plotmeans(weight~trt,xlab = "treatment",ylab = "weight", main="mean plot\nwith95% CI")- 1
- 2

随机区组设计资料的方差分析
使用例4-3的数据。
首先是构造数据,本次数据自己从书上摘录。。
weight <- c(0.82,0.65,0.51,0.73,0.54,0.23,0.43,0.34,0.28,0.41,0.21, 0.31,0.68,0.43,0.24) block <- c(rep(c("1","2","3","4","5"),each=3)) group <- c(rep(c("A","B","C"),5)) data4_4 <- data.frame(weight,block,group) head(data4_4)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
## weight block group ## 1 0.82 1 A ## 2 0.65 1 B ## 3 0.51 1 C ## 4 0.73 2 A ## 5 0.54 2 B ## 6 0.23 2 C- 1
- 2
- 3
- 4
- 5
- 6
- 7

数据一共3列,第一列是小白鼠肉瘤重量,第二列是区组因素(5个区组),第三列是分组(一共3组)
进行随机区组设计资料的方差分析(two-way anova):
fit <- aov(weight ~ block + group,data = data4_4) #随机区组设计方差分析,注意顺序 summary(fit)- 1
- 2
## Df Sum Sq Mean Sq F value Pr(>F) ## block 4 0.2284 0.05709 5.978 0.01579 * ## group 2 0.2280 0.11400 11.937 0.00397 ** ## Residuals 8 0.0764 0.00955 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
结果显示区组间自由度为4,分组间自由度为2,组内自由度为8,区组间离均差平方和为0.2284,分组间离均差平方和为0.2280,组内离均差平方和为0.0764,区组间均方为0.05709,分组间均方为0.1140,组内均方为0.00955,区组间F值=5.798,p=0.01579,分组间F值=11.937,p=0.00397,和课本一致。
拉丁方设计方差分析
使用课本例4-5的数据。
首先是构造数据,本次数据自己从书上摘录。。
psize <- c(87,75,81,75,84,66,73,81,87,85,64,79,73,73,74,78,73,77,77,68,69,74,76,73, 64,64,72,76,70,81,75,77,82,61,82,61) drug <- c("C","B","E","D","A","F","B","A","D","C","F","E","F","E","B","A","D","C", "A","F","C","B","E","D","D","C","F","E","B","A","E","D","A","F","C","B") col_block <- c(rep(1:6,6)) row_block <- c(rep(1:6,each=6)) mydata <- data.frame(psize,drug,col_block,row_block) mydata$col_block <- factor(mydata$col_block) mydata$row_block <- factor(mydata$row_block) str(mydata)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
## 'data.frame': 36 obs. of 4 variables: ## $ psize : num 87 75 81 75 84 66 73 81 87 85 ... ## $ drug : chr "C" "B" "E" "D" ... ## $ col_block: Factor w/ 6 levels "1","2","3","4",..: 1 2 3 4 5 6 1 2 3 4 ... ## $ row_block: Factor w/ 6 levels "1","2","3","4",..: 1 1 1 1 1 1 2 2 2 2 ...- 1
- 2
- 3
- 4
- 5

数据一共4列,第一列是皮肤疱疹大小,第二列是不同药物(处理因素,共5种),第三列是列区组因素,第四列是行区组因素。
进行拉丁方设计的方差分析(two-way anova):
fit <- aov(psize ~ drug + row_block + col_block, data = mydata) summary(fit)- 1
- 2
## Df Sum Sq Mean Sq F value Pr(>F) ## drug 5 667.1 133.43 3.906 0.0124 * ## row_block 5 250.5 50.09 1.466 0.2447 ## col_block 5 85.5 17.09 0.500 0.7723 ## Residuals 20 683.2 34.16 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
结果显示行区组间自由度为5,列区组间自由度为5,分组(处理因素)间自由度为5,组内自由度为20;
行区组间离均差平方和为250.5,列区组间离均差平方和为85.5,分组间离均差平方和为667.1,组内离均差平方和为0.0683.2;
行区组间均方为50.09,列区组间均方为17.09,分组间均方为133.43,组内均方为34.16,
行区组间F值=1.466,p=0.2447,列区组间F值=0.5,p=0.7723,分组间F值=3.906,p=0.0124,和课本一致。两阶段交叉设计资料方差分析
使用课本例4-6的数据。
首先是构造数据,本次数据自己从书上摘录。。
contain <- c(760,770,860,855,568,602,780,800,960,958,940,952,635,650,440,450, 528,530,800,803) phase <- rep(c("phase_1","phase_2"),10) type <- c("A","B","B","A","A","B","A","B","B","A","B","A","A","B","B","A", "A","B","B","A") testid <- rep(1:10,each=2) mydata <- data.frame(testid,phase,type,contain) str(mydata)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
## 'data.frame': 20 obs. of 4 variables: ## $ testid : int 1 1 2 2 3 3 4 4 5 5 ... ## $ phase : chr "phase_1" "phase_2" "phase_1" "phase_2" ... ## $ type : chr "A" "B" "B" "A" ... ## $ contain: num 760 770 860 855 568 602 780 800 960 958 ...- 1
- 2
- 3
- 4
- 5
mydata$testid <- factor(mydata$testid)- 1

数据一共4列,第一列是受试者id,第二列是不同阶段,第三列是测定方法,第四列是测量值。
简单看下2个阶段情况:
table(mydata$phase,mydata$type)- 1
## ## A B ## phase_1 5 5 ## phase_2 5 5- 1
- 2
- 3
- 4
进行两阶段交叉设计资料方差分析(two-way anova):
fit <- aov(contain~phase+type+testid,mydata) summary(fit)- 1
- 2
## Df Sum Sq Mean Sq F value Pr(>F) ## phase 1 490 490 9.925 0.0136 * ## type 1 198 198 4.019 0.0799 . ## testid 9 551111 61235 1240.195 1.32e-11 *** ## Residuals 8 395 49 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
结果和课本一致!
多个样本均数间的多重比较
使用课本例4-2的数据。
首先是构造数据,本次数据自己从书上摘录。。
trt<-c(rep("group1",30),rep("group2",30),rep("group3",30),rep("group4",30)) weight<-c(3.53,4.59,4.34,2.66,3.59,3.13,3.30,4.04,3.53,3.56,3.85,4.07,1.37, 3.93,2.33,2.98,4.00,3.55,2.64,2.56,3.50,3.25,2.96,4.30,3.52,3.93, 4.19,2.96,4.16,2.59,2.42,3.36,4.32,2.34,2.68,2.95,2.36,2.56,2.52, 2.27,2.98,3.72,2.65,2.22,2.90,1.98,2.63,2.86,2.93,2.17,2.72,1.56, 3.11,1.81,1.77,2.80,3.57,2.97,4.02,2.31,2.86,2.28,2.39,2.28,2.48, 2.28,3.48,2.42,2.41,2.66,3.29,2.70,2.66,3.68,2.65,2.66,2.32,2.61, 3.64,2.58,3.65,3.21,2.23,2.32,2.68,3.04,2.81,3.02,1.97,1.68,0.89, 1.06,1.08,1.27,1.63,1.89,1.31,2.51,1.88,1.41,3.19,1.92,0.94,2.11, 2.81,1.98,1.74,2.16,3.37,2.97,1.69,1.19,2.17,2.28,1.72,2.47,1.02, 2.52,2.10,3.71) data1<-data.frame(trt,weight) data1$trt <- factor(data1$trt) str(data1)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
## 'data.frame': 120 obs. of 2 variables: ## $ trt : Factor w/ 4 levels "group1","group2",..: 1 1 1 1 1 1 1 1 1 1 ... ## $ weight: num 3.53 4.59 4.34 2.66 3.59 3.13 3.3 4.04 3.53 3.56 ...- 1
- 2
- 3
数据一共两列,第一列是分组(一共四组),第二列是低密度脂蛋白测量值
进行完全随机设计资料的方差分析:
fit <- aov(weight ~ trt, data = data1) summary(fit)- 1
- 2
## Df Sum Sq Mean Sq F value Pr(>F) ## trt 3 32.16 10.719 24.88 1.67e-12 *** ## Residuals 116 49.97 0.431 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
LSD-t检验
使用超级全能的
PMCMRplus包实现,需要自己安装。library(PMCMRplus)- 1
## Warning: package 'PMCMRplus' was built under R version 4.2.1- 1
res <- lsdTest(fit) # lsdTest(weight ~ trt, data = data1) 也可以 summary(res)- 1
- 2
- 3
- 4
- 5
## ## Pairwise comparisons using Least Significant Difference Test- 1
- 2
## data: weight by trt- 1
## alternative hypothesis: two.sided- 1
## P value adjustment method: none- 1
## H0- 1
## t value Pr(>|t|) ## group2 - group1 == 0 -4.219 4.8872e-05 *** ## group3 - group1 == 0 -4.322 3.2889e-05 *** ## group4 - group1 == 0 -8.639 3.5772e-14 *** ## group3 - group2 == 0 -0.102 0.91871 ## group4 - group2 == 0 -4.420 2.2345e-05 *** ## group4 - group3 == 0 -4.318 3.3397e-05 ***- 1
- 2
- 3
- 4
- 5
- 6
- 7
## ---- 1
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
结果比SPSS的结果更加直接,给出了统计量和P值,可以非常直观的看出哪两个组之间有差别。
所以
group2和group3是没差别的,和另外两组有差别。还可以可视化结果:
plot(res)- 1

TukeyHSD
这里介绍一种
TukeyHSD方法:TukeyHSD(fit) ### 每个组之间进行比较,多重比较- 1
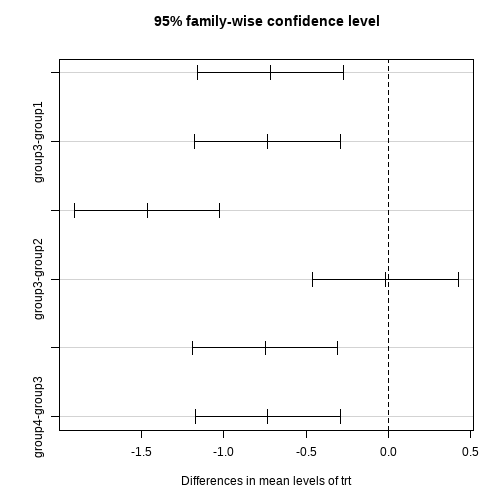
## Tukey multiple comparisons of means ## 95% family-wise confidence level ## ## Fit: aov(formula = weight ~ trt, data = data1) ## ## $trt ## diff lwr upr p adj ## group2-group1 -0.71500000 -1.1567253 -0.2732747 0.0002825 ## group3-group1 -0.73233333 -1.1740587 -0.2906080 0.0001909 ## group4-group1 -1.46400000 -1.9057253 -1.0222747 0.0000000 ## group3-group2 -0.01733333 -0.4590587 0.4243920 0.9996147 ## group4-group2 -0.74900000 -1.1907253 -0.3072747 0.0001302 ## group4-group3 -0.73166667 -1.1733920 -0.2899413 0.0001938- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
这个结果更直观,可以直接看到每个组之间的比较,后面给出了P值。
可视化结果:
plot(TukeyHSD(fit))- 1
Dunnett-t检验
使用超级全能的
PMCMRplus包实现library(PMCMRplus) res <- dunnettTest(fit) # 或者 dunnettTest(weight ~ trt, data = data1) summary(res)- 1
- 2
- 3
- 4
- 5
- 6
## ## Pairwise comparisons using Dunnett's-test for multiple ## comparisons with one control- 1
- 2
- 3
## data: weight by trt- 1
## alternative hypothesis: two.sided- 1
## P value adjustment method: single-step- 1
## H0- 1
## t value Pr(>|t|) ## group2 - group1 == 0 -4.219 0.00013135 *** ## group3 - group1 == 0 -4.322 7.7322e-05 *** ## group4 - group1 == 0 -8.639 2.1538e-14 ***- 1
- 2
- 3
- 4
## ---- 1
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
结果也是非常明显,所有组和安慰剂组相比都有意义。
可视化结果:
plot(res)- 1

SNK-q检验
还是使用超级全能的
PMCMRplus包实现。library(PMCMRplus) res <- snkTest(fit) # 或者 snkTest(weight ~ trt, data = data1) summary(res)- 1
- 2
- 3
- 4
- 5
- 6
## ## Pairwise comparisons using SNK test- 1
- 2
## data: weight by trt- 1
## alternative hypothesis: two.sided- 1
## P value adjustment method: step down- 1
## H0- 1
## q value Pr(>|q|) ## group2 - group1 == 0 -5.967 4.8872e-05 *** ## group3 - group1 == 0 -6.112 9.7010e-05 *** ## group4 - group1 == 0 -12.218 2.5524e-13 *** ## group3 - group2 == 0 -0.145 0.91871 ## group4 - group2 == 0 -6.251 6.6031e-05 *** ## group4 - group3 == 0 -6.106 3.3397e-05 ***- 1
- 2
- 3
- 4
- 5
- 6
- 7
## ---- 1
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
这个结果也很直观,可以直接看到每个组之间的比较,后面给出了P值。
可视化结果:
plot(res)- 1

多样本方差比较的Bartlett检验和Levene检验
多样本方差比较的Bartlett检验
使用课本例4-2的数据。
trt<-c(rep("group1",30),rep("group2",30),rep("group3",30),rep("group4",30)) weight<-c(3.53,4.59,4.34,2.66,3.59,3.13,3.30,4.04,3.53,3.56,3.85,4.07,1.37, 3.93,2.33,2.98,4.00,3.55,2.64,2.56,3.50,3.25,2.96,4.30,3.52,3.93, 4.19,2.96,4.16,2.59,2.42,3.36,4.32,2.34,2.68,2.95,2.36,2.56,2.52, 2.27,2.98,3.72,2.65,2.22,2.90,1.98,2.63,2.86,2.93,2.17,2.72,1.56, 3.11,1.81,1.77,2.80,3.57,2.97,4.02,2.31,2.86,2.28,2.39,2.28,2.48, 2.28,3.48,2.42,2.41,2.66,3.29,2.70,2.66,3.68,2.65,2.66,2.32,2.61, 3.64,2.58,3.65,3.21,2.23,2.32,2.68,3.04,2.81,3.02,1.97,1.68,0.89, 1.06,1.08,1.27,1.63,1.89,1.31,2.51,1.88,1.41,3.19,1.92,0.94,2.11, 2.81,1.98,1.74,2.16,3.37,2.97,1.69,1.19,2.17,2.28,1.72,2.47,1.02, 2.52,2.10,3.71) data1<-data.frame(trt,weight) data1$trt <- factor(data1$trt) str(data1)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
## 'data.frame': 120 obs. of 2 variables: ## $ trt : Factor w/ 4 levels "group1","group2",..: 1 1 1 1 1 1 1 1 1 1 ... ## $ weight: num 3.53 4.59 4.34 2.66 3.59 3.13 3.3 4.04 3.53 3.56 ...- 1
- 2
- 3
进行Bartlett检验:
bartlett.test(weight ~ trt, data = data1)- 1
## ## Bartlett test of homogeneity of variances ## ## data: weight by trt ## Bartlett's K-squared = 5.2192, df = 3, p-value = 0.1564- 1
- 2
- 3
- 4
- 5
由结果可知,P值为0.1564,不拒绝H0,不能认为不满足方差齐性!
多样本方差比较的Levene检验
使用
car包实现。library(car)- 1
## Loading required package: carData- 1
leveneTest(weight ~ trt, data = data1)- 1
## Levene's Test for Homogeneity of Variance (center = median) ## Df F value Pr(>F) ## group 3 1.493 0.2201 ## 116- 1
- 2
- 3
- 4
由结果可知,不能认为不满足方差齐性!
多因素方差分析
2 x 2 两因素析因设计资料的方差分析
使用课本例11-1的数据,自己手动摘录:
df11_1 <- data.frame( x1 = rep(c("外膜缝合","束膜缝合"), each = 10), x2 = rep(c("缝合1个月","缝合2个月"), each = 5), y = c(10,10,40,50,10,30,30,70,60,30,10,20,30,50,30,50,50,70,60,30) ) str(df11_1)- 1
- 2
- 3
- 4
- 5
- 6
- 7
## 'data.frame': 20 obs. of 3 variables: ## $ x1: chr "外膜缝合" "外膜缝合" "外膜缝合" "外膜缝合" ... ## $ x2: chr "缝合1个月" "缝合1个月" "缝合1个月" "缝合1个月" ... ## $ y : num 10 10 40 50 10 30 30 70 60 30 ...- 1
- 2
- 3
- 4
数据一共3列,第1列是缝合方法,第2列是时间,第3列是轴突通过率。

进行析因设计资料的方差分析(two-way anova):
f1 <- aov(y ~ x1 * x2, data = df11_1) summary(f1)- 1
- 2
- 3
## Df Sum Sq Mean Sq F value Pr(>F) ## x1 1 180 180 0.600 0.4499 ## x2 1 2420 2420 8.067 0.0118 * ## x1:x2 1 20 20 0.067 0.7995 ## Residuals 16 4800 300 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
结果显示了A因素主效应、B因素主效应、AB交互作用的自由度、离均差平方和、均方误差、F值、P值等,可以看到结果和课本是一致的!
简单介绍一下可视化两因素析因设计的方法:
interaction.plot(df11_1$x2, df11_1$x1, df11_1$y, type = "b", col = c("red","blue"), pch = c(12,15), xlab = "缝合时间", ylab = "轴突通过率")- 1

另外一种可视化方法:
library(gplots) attach(df11_1) plotmeans(y ~ interaction(x1,x2), connect = list(c(1,3), c(2,4)), col = c("red","darkgreen"), main = "两因素析因设计", xlab = "时间和方法的交互")- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9

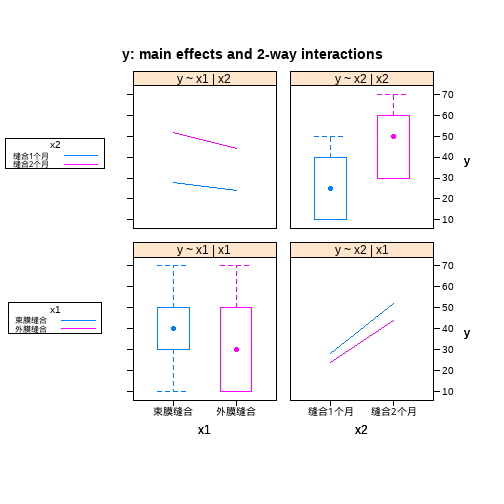
再介绍一种方法:
suppressMessages(library(HH))- 1
## Warning: package 'latticeExtra' was built under R version 4.2.1- 1
interaction2wt(y ~ x1 * x2)- 1
detach(df11_1)- 1
I x J 两因素析因设计资料的方差分析
使用课本例11-2的数据,自己手动摘录:
df11_2 <- data.frame( druga = rep(c("1mg","2.5mg","5mg"), each = 3), drugb = rep(c("5微克","15微克","30微克"),each = 9), y = c(105,80,65,75,115,80,85,120,125,115,105,80,125,130,90,65,120,100,75,95,85,135,120,150,180,190,160) ) str(df11_2)- 1
- 2
- 3
- 4
- 5
- 6
- 7
## 'data.frame': 27 obs. of 3 variables: ## $ druga: chr "1mg" "1mg" "1mg" "2.5mg" ... ## $ drugb: chr "5微克" "5微克" "5微克" "5微克" ... ## $ y : num 105 80 65 75 115 80 85 120 125 115 ...- 1
- 2
- 3
- 4
数据一共3列,第1列是a药物的剂量(3种剂量,代表3个水平),第2列是b药物的剂量(3种剂量),第3列是镇痛时间。

进行两因素三水平的析因设计资料方差分析(two-way anova):
f2 <- aov(y ~ druga * drugb, data = df11_2) summary(f2)- 1
- 2
- 3
## Df Sum Sq Mean Sq F value Pr(>F) ## druga 2 6572 3286 8.470 0.00256 ** ## drugb 2 7022 3511 9.050 0.00190 ** ## druga:drugb 4 7872 1968 5.073 0.00647 ** ## Residuals 18 6983 388 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
结果和课本也是一模一样的哦!
I x J x K 三因素析因设计资料的方差分析
使用课本例11-3的数据,
df11_3 <- foreign::read.spss("../000统计学/例11-03-5种军装热感觉5-2-2.sav", to.data.frame = T) df11_3$a <- factor(df11_3$a) str(df11_3)- 1
- 2
- 3
- 4
- 5
## 'data.frame': 100 obs. of 4 variables: ## $ b: Factor w/ 2 levels "干燥","潮湿": 1 1 1 1 1 1 1 1 1 1 ... ## $ c: Factor w/ 2 levels "静坐","活动": 1 1 1 1 1 1 1 1 1 1 ... ## $ a: Factor w/ 5 levels "1","2","3","4",..: 1 1 1 1 1 2 2 2 2 2 ... ## $ x: num 0.25 -0.25 1.25 -0.75 0.4 ... ## - attr(*, "variable.labels")= Named chr [1:4] "活动环境" "活动状态" "军装类型" "主观热感觉" ## ..- attr(*, "names")= chr [1:4] "b" "c" "a" "x" ## - attr(*, "codepage")= int 65001- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
数据一共4列,前3列分别是b因素,c因素,a因素,每个因素有不同的水平,第4列是因变量(展示的图有乱码,不影响使用)。

进行3因素析因设计资料的方差分析(three-way anova):
f3 <- aov(x ~ b * c * a, data = df11_3) summary(f3)- 1
- 2
- 3
## Df Sum Sq Mean Sq F value Pr(>F) ## b 1 9.94 9.94 23.138 6.98e-06 *** ## c 1 283.35 283.35 659.485 < 2e-16 *** ## a 4 5.20 1.30 3.024 0.0224 * ## b:c 1 12.68 12.68 29.514 5.82e-07 *** ## b:a 4 1.94 0.48 1.128 0.3491 ## c:a 4 1.48 0.37 0.862 0.4905 ## b:c:a 4 1.61 0.40 0.937 0.4472 ## Residuals 80 34.37 0.43 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
结果也是和课本一模一样。
正交设计资料的方差分析
使用课本例11-4的数据
df11_4 <- data.frame( a = rep(c("5度","25度"),each = 4), b = rep(c(0.5, 5.0), each = 2), c = c(10, 30), d = c(6.0, 8.0,8.0,6.0,8.0,6.0,6.0,8.0), x = c(86,95,91,94,91,96,83,88) ) df11_4$a <- factor(df11_4$a) df11_4$b <- factor(df11_4$b) df11_4$c <- factor(df11_4$c) df11_4$d <- factor(df11_4$d) str(df11_4)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
## 'data.frame': 8 obs. of 5 variables: ## $ a: Factor w/ 2 levels "25度","5度": 2 2 2 2 1 1 1 1 ## $ b: Factor w/ 2 levels "0.5","5": 1 1 2 2 1 1 2 2 ## $ c: Factor w/ 2 levels "10","30": 1 2 1 2 1 2 1 2 ## $ d: Factor w/ 2 levels "6","8": 1 2 2 1 2 1 1 2 ## $ x: num 86 95 91 94 91 96 83 88- 1
- 2
- 3
- 4
- 5
- 6
进行正交设计资料的方差分析:
f4 <- aov(x ~ a + b + c + d + a*b, data = df11_4) summary(f4)- 1
- 2
- 3
## Df Sum Sq Mean Sq F value Pr(>F) ## a 1 8.0 8.0 3.2 0.2155 ## b 1 18.0 18.0 7.2 0.1153 ## c 1 60.5 60.5 24.2 0.0389 * ## d 1 4.5 4.5 1.8 0.3118 ## a:b 1 50.0 50.0 20.0 0.0465 * ## Residuals 2 5.0 2.5 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
结果和课本一模一样,用R语言进行方差分析真是太简单了!!!!
嵌套设计资料的方差分析
使用课本例11-6的数据。
df <- data.frame(factor1 = factor(rep(c("A","B","C"),each=6)), factor2 = factor(rep(c(70,80,90,55,65,75,90,95,100),each=2)), y = c(82,84,91,88,85,83,65,61,62,59,56,60,71,67,75,78,85,89) ) str(df)- 1
- 2
- 3
- 4
- 5
## 'data.frame': 18 obs. of 3 variables: ## $ factor1: Factor w/ 3 levels "A","B","C": 1 1 1 1 1 1 2 2 2 2 ... ## $ factor2: Factor w/ 8 levels "55","65","70",..: 3 3 5 5 6 6 1 1 2 2 ... ## $ y : num 82 84 91 88 85 83 65 61 62 59 ...- 1
- 2
- 3
- 4
df- 1
## factor1 factor2 y ## 1 A 70 82 ## 2 A 70 84 ## 3 A 80 91 ## 4 A 80 88 ## 5 A 90 85 ## 6 A 90 83 ## 7 B 55 65 ## 8 B 55 61 ## 9 B 65 62 ## 10 B 65 59 ## 11 B 75 56 ## 12 B 75 60 ## 13 C 90 71 ## 14 C 90 67 ## 15 C 95 75 ## 16 C 95 78 ## 17 C 100 85 ## 18 C 100 89- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
factor1是一级实验因素(不同的催化剂),factor2是二级实验因素(不同的温度),y是因变量。进行嵌套实验设计的方差分析:
f <- aov(y ~ factor1/factor2, data = df) summary(f)- 1
- 2
## Df Sum Sq Mean Sq F value Pr(>F) ## factor1 2 1956.0 978.0 177.82 5.83e-08 *** ## factor1:factor2 6 401.0 66.8 12.15 0.000716 *** ## Residuals 9 49.5 5.5 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
结果和课本相同。
裂区设计资料的方差分析
使用课本例11-7的数据。这是一个完全随机的2*2裂区设计。
df <- data.frame(factorA = factor(rep(c("a1","a2"),each=10)), factorB = factor(rep(c("b1","b2"),10)), id = factor(rep(c(1:10),each=2)), y = c(15.75,19.00,15.50,20.75,15.50,18.50,17.00,20.50,16.50,20.00, 18.25,22.25,18.50,21.50,19.75,23.50,21.50,24.75,20.75,23.75) ) str(df)- 1
- 2
- 3
- 4
- 5
- 6
- 7
## 'data.frame': 20 obs. of 4 variables: ## $ factorA: Factor w/ 2 levels "a1","a2": 1 1 1 1 1 1 1 1 1 1 ... ## $ factorB: Factor w/ 2 levels "b1","b2": 1 2 1 2 1 2 1 2 1 2 ... ## $ id : Factor w/ 10 levels "1","2","3","4",..: 1 1 2 2 3 3 4 4 5 5 ... ## $ y : num 15.8 19 15.5 20.8 15.5 ...- 1
- 2
- 3
- 4
- 5
df- 1
## factorA factorB id y ## 1 a1 b1 1 15.75 ## 2 a1 b2 1 19.00 ## 3 a1 b1 2 15.50 ## 4 a1 b2 2 20.75 ## 5 a1 b1 3 15.50 ## 6 a1 b2 3 18.50 ## 7 a1 b1 4 17.00 ## 8 a1 b2 4 20.50 ## 9 a1 b1 5 16.50 ## 10 a1 b2 5 20.00 ## 11 a2 b1 6 18.25 ## 12 a2 b2 6 22.25 ## 13 a2 b1 7 18.50 ## 14 a2 b2 7 21.50 ## 15 a2 b1 8 19.75 ## 16 a2 b2 8 23.50 ## 17 a2 b1 9 21.50 ## 18 a2 b2 9 24.75 ## 19 a2 b1 10 20.75 ## 20 a2 b2 10 23.75- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
进行裂区设计的方差分析:
f <- aov(y ~ factorA * factorB + Error(id/factorB), data = df) summary(f)- 1
- 2
## ## Error: id ## Df Sum Sq Mean Sq F value Pr(>F) ## factorA 1 63.01 63.01 28.01 0.000735 *** ## Residuals 8 18.00 2.25 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Error: id:factorB ## Df Sum Sq Mean Sq F value Pr(>F) ## factorB 1 63.01 63.01 252.05 2.48e-07 *** ## factorA:factorB 1 0.11 0.11 0.45 0.521 ## Residuals 8 2.00 0.25 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
结果同课本相同。
重复测量方差分析
重复测量数据两因素两水平的方差分析
使用课本例12-1的数据,直接读取:
df12_1 <- foreign::read.spss("../000统计学/12-1.sav", to.data.frame = T)- 1
## re-encoding from CP936- 1
str(df12_1)- 1
## 'data.frame': 20 obs. of 5 variables: ## $ n : num 1 2 3 4 5 6 7 8 9 10 ... ## $ x1 : num 130 124 136 128 122 118 116 138 126 124 ... ## $ x2 : num 114 110 126 116 102 100 98 122 108 106 ... ## $ group: Factor w/ 2 levels "处理组","对照组": 1 1 1 1 1 1 1 1 1 1 ... ## $ d : num 16 14 10 12 20 18 18 16 18 18 ... ## - attr(*, "variable.labels")= Named chr [1:5] "编号" "治疗前血压" "治疗后血压" "组别" ... ## ..- attr(*, "names")= chr [1:5] "n" "x1" "x2" "group" ... ## - attr(*, "codepage")= int 936- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
数据一共5列(第5列是自己算出来的,其实原始数据只有4列),第1 列是编号,第2列是治疗前血压,第3例是治疗后血压,第4列是分组,第5列是血压前后差值。

进行重复测量数据两因素两水平的方差分析前,先把数据转换一下格式:
library(tidyverse)- 1
df12_11 <- df12_1[,1:4] %>% pivot_longer(cols = 2:3,names_to = "time",values_to = "hp") %>% mutate_if(is.character, as.factor) df12_11$n <- factor(df12_11$n) str(df12_11)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
## tibble [40 × 4] (S3: tbl_df/tbl/data.frame) ## $ n : Factor w/ 20 levels "1","2","3","4",..: 1 1 2 2 3 3 4 4 5 5 ... ## $ group: Factor w/ 2 levels "处理组","对照组": 1 1 1 1 1 1 1 1 1 1 ... ## $ time : Factor w/ 2 levels "x1","x2": 1 2 1 2 1 2 1 2 1 2 ... ## $ hp : num [1:40] 130 114 124 110 136 126 128 116 122 102 ...- 1
- 2
- 3
- 4
- 5

转换后的数据格式如上,只截取了一部分。
进行重复测量数据两因素两水平的方差分析:
hp是因变量,time是测量时间(治疗前和治疗后各测量一次),group是分组因素(两种治疗方法),n是受试者编号。
f1 <- aov(hp ~ time * group + Error(n/(time)), data = df12_11) summary(f1)- 1
- 2
- 3
## ## Error: n ## Df Sum Sq Mean Sq F value Pr(>F) ## group 1 202.5 202.5 1.574 0.226 ## Residuals 18 2315.4 128.6 ## ## Error: n:time ## Df Sum Sq Mean Sq F value Pr(>F) ## time 1 1020.1 1020.1 55.01 7.08e-07 *** ## time:group 1 348.1 348.1 18.77 0.000401 *** ## Residuals 18 333.8 18.5 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
结果输出了两张表,第二个是测量前后比较与交互作用的方差分析表,第一个是处理组与对照组比较的方差分析表,可以看到结果和课本是一样的!
用图形方式展示重复测量的结果:
with(df12_11, interaction.plot(time, group, hp, type = "b", col = c("red","blue"), pch = c(12,16), main = "两因素两水平重复测量方差分析"))- 1
- 2
- 3
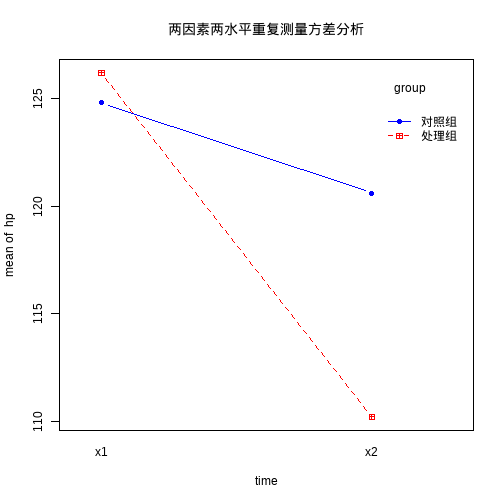
或者用箱线图展示结果:
boxplot(hp ~ group*time, data = df12_11, col = c("gold","green"), main = "两因素两水平重复测量方差分析")- 1
- 2

重复测量数据两因素多水平的分析
使用课本例12-3的数据,直接读取:
df12_3 <- foreign::read.spss("../000统计学/例12-03.sav",to.data.frame = T) str(df12_3)- 1
- 2
- 3
## 'data.frame': 15 obs. of 7 variables: ## $ No : num 1 2 3 4 5 6 7 8 9 10 ... ## $ group: Factor w/ 3 levels "A","B","C": 1 1 1 1 1 2 2 2 2 2 ... ## $ t0 : num 120 118 119 121 127 121 122 128 117 118 ... ## $ t1 : num 108 109 112 112 121 120 121 129 115 114 ... ## $ t2 : num 112 115 119 119 127 118 119 126 111 116 ... ## $ t3 : num 120 126 124 126 133 131 129 135 123 123 ... ## $ t4 : num 117 123 118 120 126 137 133 142 131 133 ... ## - attr(*, "variable.labels")= Named chr [1:7] "\xd0\xf2\xba\xc5" "\xd7\xe9\xb1\xf0" "" "" ... ## ..- attr(*, "names")= chr [1:7] "No" "group" "t0" "t1" ...- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
## 'data.frame': 15 obs. of 7 variables: ## $ No : num 1 2 3 4 5 6 7 8 9 10 ... ## $ group: Factor w/ 3 levels "A","B","C": 1 1 1 1 1 2 2 2 2 2 ... ## $ t0 : num 120 118 119 121 127 121 122 128 117 118 ... ## $ t1 : num 108 109 112 112 121 120 121 129 115 114 ... ## $ t2 : num 112 115 119 119 127 118 119 126 111 116 ... ## $ t3 : num 120 126 124 126 133 131 129 135 123 123 ... ## $ t4 : num 117 123 118 120 126 137 133 142 131 133 ... ## - attr(*, "variable.labels")= Named chr [1:7] "序号" "组别" "" "" ... ## ..- attr(*, "names")= chr [1:7] "No" "group" "t0" "t1" ...- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
数据一共7列,第1列是患者编号,第2列是诱导方法(3种),第3-7列是5个时间点的血压。

首先转换数据格式:
library(tidyverse) df12_31 <- df12_3 %>% pivot_longer(cols = 3:7, names_to = "times", values_to = "hp") df12_31$No <- factor(df12_31$No) df12_31$times <- factor(df12_31$times) str(df12_31)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
## tibble [75 × 4] (S3: tbl_df/tbl/data.frame) ## $ No : Factor w/ 15 levels "1","2","3","4",..: 1 1 1 1 1 2 2 2 2 2 ... ## $ group: Factor w/ 3 levels "A","B","C": 1 1 1 1 1 1 1 1 1 1 ... ## $ times: Factor w/ 5 levels "t0","t1","t2",..: 1 2 3 4 5 1 2 3 4 5 ... ## $ hp : num [1:75] 120 108 112 120 117 118 109 115 126 123 ...- 1
- 2
- 3
- 4
- 5

转换后的格式见上图,只截取了部分。
进行方差分析:
f2 <- aov(hp ~ times * group + Error(No/(times)), data = df12_31) summary(f2)- 1
- 2
- 3
## ## Error: No ## Df Sum Sq Mean Sq F value Pr(>F) ## group 2 912.2 456.1 5.783 0.0174 * ## Residuals 12 946.5 78.9 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Error: No:times ## Df Sum Sq Mean Sq F value Pr(>F) ## times 4 2336.5 584.1 106.6 < 2e-16 *** ## times:group 8 837.6 104.7 19.1 1.62e-12 *** ## Residuals 48 263.1 5.5 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
输出结果是两张表格,第1个是不同诱导方法患者血压比较的方差分析表,第2个是麻醉诱导时相及其与诱导方法交互作用的方差分析表。
结果和课本是一样的!具体意义解读请认真学习医学统计学相关知识。
用图形方式展示重复测量的结果:
with(df12_31, interaction.plot(times, group, hp, type = "b", col = c("red","blue","green"), pch = c(12,16,20), main = "两因素多水平重复测量方差分析"))- 1
- 2
- 3
- 4
- 5

或者用箱线图展示结果:
boxplot(hp ~ group*times, data = df12_31, col = c("gold","green","black"), main = "两因素多水平重复测量方差分析")- 1
- 2

重复测量数据的多重比较
使用课本例12-1的数据,直接读取:
df12_3 <- foreign::read.spss("../000统计学/例12-03.sav",to.data.frame = T) str(df12_3)- 1
- 2
- 3
## 'data.frame': 15 obs. of 7 variables: ## $ No : num 1 2 3 4 5 6 7 8 9 10 ... ## $ group: Factor w/ 3 levels "A","B","C": 1 1 1 1 1 2 2 2 2 2 ... ## $ t0 : num 120 118 119 121 127 121 122 128 117 118 ... ## $ t1 : num 108 109 112 112 121 120 121 129 115 114 ... ## $ t2 : num 112 115 119 119 127 118 119 126 111 116 ... ## $ t3 : num 120 126 124 126 133 131 129 135 123 123 ... ## $ t4 : num 117 123 118 120 126 137 133 142 131 133 ... ## - attr(*, "variable.labels")= Named chr [1:7] "\xd0\xf2\xba\xc5" "\xd7\xe9\xb1\xf0" "" "" ... ## ..- attr(*, "names")= chr [1:7] "No" "group" "t0" "t1" ...- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
数据一共7列,第1列是患者编号,第2列是诱导方法(3种),第3-7列是5个时间点的血压。
首先转换数据格式:
library(reshape2)- 1
df.l <- melt(df12_3, id.vars = c("No","group"), variable.name = "times", value.name = "hp") df.l$No <- factor(df.l$No) str(df.l)- 1
- 2
- 3
- 4
- 5
- 6
## 'data.frame': 75 obs. of 4 variables: ## $ No : Factor w/ 15 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ... ## $ group: Factor w/ 3 levels "A","B","C": 1 1 1 1 1 2 2 2 2 2 ... ## $ times: Factor w/ 5 levels "t0","t1","t2",..: 1 1 1 1 1 1 1 1 1 1 ... ## $ hp : num 120 118 119 121 127 121 122 128 117 118 ...- 1
- 2
- 3
- 4
- 5
head(df.l)- 1
## No group times hp ## 1 1 A t0 120 ## 2 2 A t0 118 ## 3 3 A t0 119 ## 4 4 A t0 121 ## 5 5 A t0 127 ## 6 6 B t0 121- 1
- 2
- 3
- 4
- 5
- 6
- 7
进行重复测量方差分析,默认方法不能输出球形检验的结果,所以我更推荐
rstatix提供的方法:# 默认 f <- aov(hp ~ group*times + Error(No/times), data = df.l) summary(f)- 1
- 2
- 3
## ## Error: No ## Df Sum Sq Mean Sq F value Pr(>F) ## group 2 912.2 456.1 5.783 0.0174 * ## Residuals 12 946.5 78.9 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Error: No:times ## Df Sum Sq Mean Sq F value Pr(>F) ## times 4 2336.5 584.1 106.6 < 2e-16 *** ## group:times 8 837.6 104.7 19.1 1.62e-12 *** ## Residuals 48 263.1 5.5 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
# rstatix library(rstatix)- 1
- 2
anova_test(data = df.l, dv = hp, wid = No, within = times, between = group )- 1
- 2
- 3
- 4
- 5
- 6
## ANOVA Table (type II tests) ## ## $ANOVA ## Effect DFn DFd F p p<.05 ges ## 1 group 2 12 5.783 1.70e-02 * 0.430 ## 2 times 4 48 106.558 3.02e-23 * 0.659 ## 3 group:times 8 48 19.101 1.62e-12 * 0.409 ## ## $`Mauchly's Test for Sphericity` ## Effect W p p<.05 ## 1 times 0.293 0.178 ## 2 group:times 0.293 0.178 ## ## $`Sphericity Corrections` ## Effect GGe DF[GG] p[GG] p[GG]<.05 HFe DF[HF] p[HF] ## 1 times 0.679 2.71, 32.58 1.87e-16 * 0.896 3.59, 43.03 4.65e-21 ## 2 group:times 0.679 5.43, 32.58 4.26e-09 * 0.896 7.17, 43.03 2.04e-11 ## p[HF]<.05 ## 1 * ## 2 *- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
画图展示:
library(ggplot2) library(dplyr) df.l |> group_by(times,group) |> summarise(mm=mean(hp)) |> ggplot(aes(times,mm))+ geom_line(aes(group=group,color=group),size=1.2)+ theme_bw()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
## `summarise()` has grouped output by 'times'. You can override using ## the `.groups` argument.- 1
- 2

接下来是重复测量数据的多重比较,课本中分成了3个方面。
组间差别多重比较
LSD/SNK/Tukey/Dunnett/Bonferroni等方法都可以,和多个均数比较的多重检验一样。library(PMCMRplus) summary(lsdTest(hp ~ group, data = df.l))- 1
- 2
- 3
## ## Pairwise comparisons using Least Significant Difference Test- 1
- 2
## data: hp by group- 1
## alternative hypothesis: two.sided- 1
## P value adjustment method: none- 1
## H0- 1
## t value Pr(>|t|) ## B - A == 0 2.175 0.0329218 * ## C - A == 0 3.860 0.0002446 *** ## C - B == 0 1.686 0.0962097 .- 1
- 2
- 3
- 4
## ---- 1
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
P值和课本不太一样,但是结论是一样的,A组和B组之间,A组和C组之间有差别,B组和C组之间没有差别。
时间趋势比较
重复测量方差分析可以采取正交多项式来探索时间变化趋势,具体的内涵解读可以参考冯国双老师的这篇文章:https://mp.weixin.qq.com/s/ndinwbDJsHjAelvNfwqgwA
在R里面进行正交多项式的探索略显复杂,首先定义要对时间变量(这里是times)进行正交多项式转变,我们这里有5个时间点,所以是1次方到4次方:
contrasts(df.l$times) <- contr.poly(5) contrasts(df.l$times)- 1
- 2
## .L .Q .C ^4 ## t0 -6.324555e-01 0.5345225 -3.162278e-01 0.1195229 ## t1 -3.162278e-01 -0.2672612 6.324555e-01 -0.4780914 ## t2 -3.510833e-17 -0.5345225 1.755417e-16 0.7171372 ## t3 3.162278e-01 -0.2672612 -6.324555e-01 -0.4780914 ## t4 6.324555e-01 0.5345225 3.162278e-01 0.1195229- 1
- 2
- 3
- 4
- 5
- 6
然后继续进行方差分析,此时是单纯探索时间对因变量的影响,所以注意formula的形式:
# A组 f1 <- aov(hp ~ times, data = df.l[df.l$group=="A",]) # 分别看不同次方的结果 summary(f1, split=list(times=list(liner=1,quadratic=2,cubic=3,biquadrate=4)))- 1
- 2
- 3
- 4
- 5
- 6
## Df Sum Sq Mean Sq F value Pr(>F) ## times 4 475.4 118.9 5.580 0.003486 ** ## times: liner 1 84.5 84.5 3.967 0.060229 . ## times: quadratic 1 26.4 26.4 1.240 0.278655 ## times: cubic 1 364.5 364.5 17.113 0.000511 *** ## times: biquadrate 1 0.0 0.0 0.001 0.972627 ## Residuals 20 426.0 21.3 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
# B组 f2 <- aov(hp ~ times, data = df.l[df.l$group=="B",]) summary(f2, split=list(times=list(liner=1,quadratic=2,cubic=3,biquadrate=4)))- 1
- 2
- 3
## Df Sum Sq Mean Sq F value Pr(>F) ## times 4 1017.0 254.3 9.757 0.000152 *** ## times: liner 1 662.5 662.5 25.421 6.24e-05 *** ## times: quadratic 1 296.2 296.2 11.367 0.003034 ** ## times: cubic 1 3.9 3.9 0.150 0.702229 ## times: biquadrate 1 54.4 54.4 2.088 0.163954 ## Residuals 20 521.2 26.1 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
# C组 f3 <- aov(hp ~ times+Error(No/times), data = df.l[df.l$group=="C",]) summary(f3, split=list(times=list(liner=1,quadratic=2,cubic=3,biquadrate=4)))- 1
- 2
- 3
## ## Error: No ## Df Sum Sq Mean Sq F value Pr(>F) ## Residuals 4 98 24.5 ## ## Error: No:times ## Df Sum Sq Mean Sq F value Pr(>F) ## times 4 1681.6 420.4 40.915 3.28e-08 *** ## times: liner 1 403.3 403.3 39.249 1.13e-05 *** ## times: quadratic 1 41.7 41.7 4.054 0.0612 . ## times: cubic 1 605.5 605.5 58.931 9.43e-07 *** ## times: biquadrate 1 631.1 631.1 61.425 7.23e-07 *** ## Residuals 16 164.4 10.3 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
可以看到结果和课本差异很大,关于这方面的资料较少,如果有大神知道,欢迎指教!
时间点比较
课本说因为事后检验重复次数太多难以承受,但是我们用计算机很快,所以用事后检验也没什么问题。
事后检验可以参考组间比较,根据组别进行分组,分组比较不同时间点的差别。
事前检验课本采用配对t检验,全都和t0的数据进行比较。
事前检验使用
rstatix包解决:library(rstatix) df.l |> group_by(group) |> t_test(hp ~ times, ref.group = "t0",paired = T)- 1
- 2
- 3
- 4
- 5
## # A tibble: 12 × 11 ## group .y. group1 group2 n1 n2 statistic df p p.adj p.adj…¹ ## *## 1 A hp t0 t1 5 5 8.35 4 1 e-3 4 e-3 ** ## 2 A hp t0 t2 5 5 1.77 4 1.52e-1 3.04e-1 ns ## 3 A hp t0 t3 5 5 -3.64 4 2.2 e-2 6.6 e-2 ns ## 4 A hp t0 t4 5 5 0.147 4 8.9 e-1 8.9 e-1 ns ## 5 B hp t0 t1 5 5 1.72 4 1.6 e-1 1.6 e-1 ns ## 6 B hp t0 t2 5 5 4.35 4 1.2 e-2 2.4 e-2 * ## 7 B hp t0 t3 5 5 -8.37 4 1 e-3 3 e-3 ** ## 8 B hp t0 t4 5 5 -16.7 4 7.47e-5 2.99e-4 *** ## 9 C hp t0 t1 5 5 1.44 4 2.23e-1 2.92e-1 ns ## 10 C hp t0 t2 5 5 4.75 4 9 e-3 2.8 e-2 * ## 11 C hp t0 t3 5 5 -5.12 4 7 e-3 2.8 e-2 * ## 12 C hp t0 t4 5 5 -1.80 4 1.46e-1 2.92e-1 ns ## # … with abbreviated variable name ¹p.adj.signif - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
直接给出3组的结果,和课本一模一样~
协方差分析
今天继续学习使用R语言进行医学统计学分析,今天要学习的内容是协方差分析,还是使用孙振球主编的《医学统计学》第4版的数据,封面如下:
协方差分析的使用条件:各变量服从正态分布,各变量相互独立,各样本总体方差齐;各总体客观存在因变量对协变量的线性回归关系且斜率相同(回归线平行)。
完全随机设计资料的协方差分析
使用课本例13-1的例子。
首先是读取数据,本次数据手动录入:
df13_1 <- data.frame(x1=c(10.8,11.6,10.6,9.0,11.2,9.9,10.6,10.4,9.6,10.5,10.6,9.9,9.5,9.7,10.7,9.2,10.5,11.0,10.1,10.7,8.5,10.0,10.4,9.7,9.4,9.2,10.5,11.2,9.6,8.0), y1=c(9.4,9.7,8.7,7.2,10.0,8.5,8.3,8.1,8.5,9.1,9.2,8.4,7.6,7.9,8.8,7.4,8.6,9.2,8.0,8.5,7.3,8.3,8.6,8.7,7.6,8.0,8.8,9.5,8.2,7.2), x2=c(10.4,9.7,9.9,9.8,11.1,8.2,8.8,10.0,9.0,9.4,8.9,10.3,9.3,9.2,10.9,9.2,9.2,10.4,11.2,11.1,11.0,8.6,9.3,10.3,10.3,9.8,10.5,10.7,10.4,9.4), y2=c(9.2,9.1,8.9,8.6,9.9,7.1,7.8,7.9,8.0,9.0,7.9,8.9,8.9,8.1,10.2,8.5,9.0,8.9,9.8,10.1,8.5,8.1,8.6,8.9,9.6,8.1,9.9,9.3,8.7,8.7), x3=c(9.8,11.2,10.7,9.6,10.1,9.8,10.1,10.3,11.0,10.5,9.2,10.1,10.4,10.0,8.4,10.1,9.3,10.5,11.1,10.5,9.7,9.2,9.3,10.4,10.0,10.3,9.9,9.4,8.3,9.2), y3=c(7.6,7.9,9.0,7.8,8.5,7.5,8.3,8.2,8.4,8.1,7.0,7.7,8.0,6.6,6.1,8.1,7.8,8.4,8.2,8.0,7.6,6.9,6.7,8.1,7.4,8.2,7.6,7.8,6.6,7.2) )- 1
- 2
- 3
- 4
- 5
- 6
- 7
看一下数据结构:
str(df13_1)- 1
## 'data.frame': 30 obs. of 6 variables: ## $ x1: num 10.8 11.6 10.6 9 11.2 9.9 10.6 10.4 9.6 10.5 ... ## $ y1: num 9.4 9.7 8.7 7.2 10 8.5 8.3 8.1 8.5 9.1 ... ## $ x2: num 10.4 9.7 9.9 9.8 11.1 8.2 8.8 10 9 9.4 ... ## $ y2: num 9.2 9.1 8.9 8.6 9.9 7.1 7.8 7.9 8 9 ... ## $ x3: num 9.8 11.2 10.7 9.6 10.1 9.8 10.1 10.3 11 10.5 ... ## $ y3: num 7.6 7.9 9 7.8 8.5 7.5 8.3 8.2 8.4 8.1 ...- 1
- 2
- 3
- 4
- 5
- 6
- 7
可以看到一共6列,和课本上面的一模一样,分别是x1,y1,x2,y2,x3,y3。
接下来为了进行方差分析,需要变为长数据,把所有的x放在1列,所有的y放在1列,还有一列是组别:
如果大家还对长款数据转换不了解的,赶紧翻看之前的推文。
这是一个非常重要且使用频率极高的技能!
suppressPackageStartupMessages(library(tidyverse)) df13_11 <- df13_1 %>% pivot_longer(cols = everything(), # 变长 names_to = c(".value","group"), names_pattern = "(.)(.)" ) %>% mutate(group = as.factor(group)) # 组别变为因子型 glimpse(df13_11) # 查看数据结构,神奇!- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
## Rows: 90 ## Columns: 3 ## $ group1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1… ## $ x 10.8, 10.4, 9.8, 11.6, 9.7, 11.2, 10.6, 9.9, 10.7, 9.0, 9.8, 9.6… ## $ y 9.4, 9.2, 7.6, 9.7, 9.1, 7.9, 8.7, 8.9, 9.0, 7.2, 8.6, 7.8, 10.0… - 1
- 2
- 3
- 4
- 5
所有的x放在1列,所有的y放在1列,还有一列是组别!
然后就是进行单因素协方差分析:
fit <- aov(y ~ x + group, data = df13_11) # 注意公式的写法,一定是把协变量放在主变量前面! summary(fit)- 1
- 2
## Df Sum Sq Mean Sq F value Pr(>F) ## x 1 29.06 29.057 171.20 <2e-16 *** ## group 2 19.85 9.925 58.48 <2e-16 *** ## Residuals 86 14.60 0.170 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
得到的结果和课本是一样的,组内ss=14.60, ms=0.170, v=86, 修正均数ss=19.85, ms=9.925, v=2, F=58.48,拒绝H0,接受H1,可以认为在扣除初始(基线)糖化血红蛋白含量的影响后,3组患者的总体降糖均数有差别。
但实际上这个结果是1型方差分析的结果,和课本上(SPSS默认3型,可参考推文:R语言做方差分析的注意事项)有一些不同之处,如果要完全一样,可以使用
car::Anova()转化一下:car::Anova(fit)- 1
## Anova Table (Type II tests) ## ## Response: y ## Sum Sq Df F value Pr(>F) ## x 30.183 1 177.83 < 2.2e-16 *** ## group 19.851 2 58.48 < 2.2e-16 *** ## Residuals 14.596 86 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
这样就是3型方差分析的结果了。
结果的可视化可以使用
HH包:library(HH)- 1
一行代码即可:
ancovaplot(y ~ x + group, data = df13_11)- 1

但其实我们也可以用
ggplot2来画,可能更好看一点:theme_set(theme_minimal()) p1 <- ggplot(df13_11, aes(x=x,y=y))+ geom_point(aes(color=group,shape=group))+ geom_smooth(method = "lm",se=F,aes(color=group))+ labs(y=NULL) p2 <- ggplot(df13_11, aes(x=x,y=y))+ geom_point(aes(color=group,shape=group))+ geom_smooth(method = "lm",se=F,aes(color=group))+ facet_wrap(~group) library(patchwork)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
## ## Attaching package: 'patchwork'- 1
- 2
## The following object is masked from 'package:MASS': ## ## area- 1
- 2
- 3
p2 + p1 + plot_layout(guides = 'collect',widths = c(3, 1))- 1
## `geom_smooth()` using formula 'y ~ x'- 1
## `geom_smooth()` using formula 'y ~ x'- 1

好看是好看,但是很明显不如
HH简洁啊!随机区组设计资料的协方差分析
使用课本例13-2的数据。
df <- foreign::read.spss("../000统计学/例13-02.sav",to.data.frame = T,reencode = "utf-8")- 1
## re-encoding from utf-8- 1
df$block <- factor(df$block) str(df)- 1
- 2
- 3
## 'data.frame': 36 obs. of 4 variables: ## $ x : num 257 272 210 300 262 ... ## $ y : num 27 41.7 25 52 14.5 48.8 48 9.5 37 56.5 ... ## $ group: Factor w/ 3 levels "A....","B....",..: 1 1 1 1 1 1 1 1 1 1 ... ## $ block: Factor w/ 12 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ... ## - attr(*, "variable.labels")= Named chr [1:4] "..ʳ.." ".........." "........" "......" ## ..- attr(*, "names")= chr [1:4] "x" "y" "group" "block"- 1
- 2
- 3
- 4
- 5
- 6
- 7
head(df)- 1
## x y group block ## 1 256.9 27.0 A.... 1 ## 2 271.6 41.7 A.... 2 ## 3 210.2 25.0 A.... 3 ## 4 300.1 52.0 A.... 4 ## 5 262.2 14.5 A.... 5 ## 6 304.4 48.8 A.... 6- 1
- 2
- 3
- 4
- 5
- 6
- 7
进行随机区组设计的协方差分析:
fit <- aov(y ~ x + block + group, data = df) # 注意顺序 summary(fit)- 1
- 2
## Df Sum Sq Mean Sq F value Pr(>F) ## x 1 69073 69073 651.823 < 2e-16 *** ## block 11 4024 366 3.452 0.00711 ** ## group 2 464 232 2.189 0.13692 ## Residuals 21 2225 106 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
car::Anova(fit)- 1
## Anova Table (Type II tests) ## ## Response: y ## Sum Sq Df F value Pr(>F) ## x 6174.2 1 58.2643 1.733e-07 *** ## block 3765.3 11 3.2302 0.01009 * ## group 463.9 2 2.1891 0.13692 ## Residuals 2225.4 21 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
结果和课本一致。
本文首发于公众号:医学和生信笔记,完美观看体验请至公众号查看本文。
医学和生信笔记,专注R语言在临床医学中的使用,R语言数据分析和可视化。
-
相关阅读:
【汇编语言实战】一元二次方程ax2+bx+c=0求解(含源码与过程截屏,可修改参数)
Java学习 5.习题2.
爬楼梯(动态规划)
Flutter的Platform介绍-跨平台开发,如何根据不同平台创建不同UI和行为
九州云亮相全球边缘计算大会,深耕边缘领域赋能产业未来新生态
学习工业设计,你需要知道这些
医依通小程序项目总结
SpringMvc-HttpMessageConverter接口
LVDS 转 MIPI 主桥芯片1 概述 GM8829C
MySQL的组成与三种log
- 原文地址:https://blog.csdn.net/Ayue0616/article/details/127588500
