4-11 Isomorphic (10分)

Two trees, T1 and T2, are isomorphic if T1 can be transformed into T2 by swapping left and right children of (some of the) nodes in T1. For instance, the two trees in Figure 1 are isomorphic because they are the same if the children of A, B, and G, but not the other nodes, are swapped. Give a polynomial time algorithm to decide if two trees are isomorphic.

Format of functions:

int Isomorphic( Tree T1, Tree T2 );

where Tree is defined as the following:

typedef struct TreeNode *Tree;
 
struct TreeNode { ElementType Element; Tree Left; Tree Right; };

The function is supposed to return 1 if T1 and T2 are indeed isomorphic, or 0 if not.

Sample program of judge:

#include  
#include  
 
typedef char ElementType;
typedef struct TreeNode *Tree; 
struct TreeNode { 
    ElementType Element; 
    Tree Left; 
    Tree Right; 
}; 
 
Tree BuildTree(); /* details omitted */ 
int Isomorphic( Tree T1, Tree T2 ); 
 
int main() 
{ Tree T1, T2; 
T1 = BuildTree(); 
T2 = BuildTree(); 
printf(“%d\n”, Isomorphic(T1, T2));
return 0; } 
 
/* Your function will be put here */

Sample Output 1 (for the trees shown in Figure 1):

1

Sample Output 2 (for the trees shown in Figure 2):

0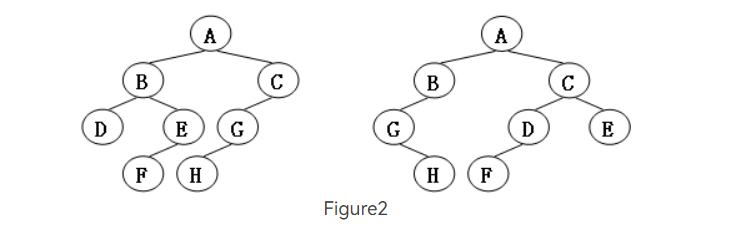

 

伪代码：

int Isomorphic(Tree R1,Tree R2)
{
    if(都是空树) return 1 ; //同构
    if(一个树为空树，一个不是空树) return 0 ; //不同构
    if(树根的值本身不相同) return 0 ;
    if(左子树都为空)/*不需要swap*/
        return Isomorphic(R1->Right,R2->Right);//只需要向下判断右子树 
    /*能执行到这里说明左子树不同时为空*/   
    if( 左子树同时不为空 && 左子树的值相同 )/*此时不需要swap*/
        return Isomorphic(R1->Right,R2->Right)&& Isomorphic(R1->Lift,R2->Lift);/*判断左左、右右子树是否同构*/
    /*执行到这里，有两种可能：左子树一个为空一个不为空 或 左子树同时不为空但是他们元素的值不同，这时就需要swap了*/
    return Isomorphic(R1->Lift,R2->Right)&&Isomorphic(R1->Right,R2->Lift);

代码：

int Isomorphic( Tree T1, Tree T2 )
{
    if(!T1&&!T2)return 1;//同时为空树
    if((T1&&!T2)||(!T1&&T2))return 0;//一个是空树，一个不是空树
    if(T1->Element!=T2->Element)return 0;//树根的值不一样
 
    if(!T1->Left&&!T2->Left)return Isomorphic(T1->Right,T2->Right);//左树同时为空，则判断右树
    else if(T1->Left&&!T2->Left)return Isomorphic(T2->Right,T1->Left);//左树一个为空一个不为空
    else if((!T1->Left&&T2->Left))return Isomorphic(T1->Right,T2->Left);
    //左树同时不为空
        if(T1->Left->Element==T1->Left->Element)
            return Isomorphic(T1->Left,T2->Left)&&Isomorphic(T1->Right,T2->Right);
        return Isomorphic(T1->Left,T2->Right)&&Isomorphic(T1->Right,T2->Left);
}

评价： 

问题看着挺难，但是把问题想清楚就容易很多了。