R语言和医学统计学（5）：多因素方差分析

本文首发于公众号：医学和生信笔记，完美观看体验请至公众号查看本文。

医学和生信笔记，专注R语言在临床医学中的使用，R语言数据分析和可视化。

前言

这是R语言和医学统计学的第5篇内容。

主要是用R语言复现课本中的例子。我使用的课本是孙振球主编的《医学统计学》第4版，封面如下：

2 x 2 两因素析因设计资料的方差分析

使用课本例11-1的数据，自己手动摘录：

df11_1 <- data.frame(
  x1 = rep(c("外膜缝合","束膜缝合"), each = 10),
  x2 = rep(c("缝合1个月","缝合2个月"), each = 5),
  y = c(10,10,40,50,10,30,30,70,60,30,10,20,30,50,30,50,50,70,60,30)
)

str(df11_1)
## 'data.frame':	20 obs. of  3 variables:
##  $ x1: chr  "外膜缝合" "外膜缝合" "外膜缝合" "外膜缝合" ...
##  $ x2: chr  "缝合1个月" "缝合1个月" "缝合1个月" "缝合1个月" ...
##  $ y : num  10 10 40 50 10 30 30 70 60 30 ...
1
2
3
4
5
6
7
8
9
10
11

数据一共3列，第1列是缝合方法，第2列是时间，第3列是轴突通过率。

进行析因设计资料的方差分析：

f1 <- aov(y ~ x1 * x2, data = df11_1)

summary(f1)
##             Df Sum Sq Mean Sq F value Pr(>F)  
## x1           1    180     180   0.600 0.4499  
## x2           1   2420    2420   8.067 0.0118 *
## x1:x2        1     20      20   0.067 0.7995  
## Residuals   16   4800     300                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1
2
3
4
5
6
7
8
9
10

结果显示了A因素主效应、B因素主效应、AB交互作用的自由度、离均差平方和、均方误差、F值、P值等，可以看到结果和课本是一致的！

简单介绍一下可视化两因素析因设计的方法：

interaction.plot(df11_1$x2, df11_1$x1, df11_1$y, type = "b", col = c("red","blue"), pch = c(12,15), xlab = "缝合时间", ylab = "轴突通过率")
1

另外一种可视化方法：

library(gplots)
## 
## 载入程辑包：'gplots'
## The following object is masked from 'package:stats':
## 
##     lowess

attach(df11_1)

plotmeans(y ~ interaction(x1,x2),
          connect = list(c(1,3), c(2,4)),
          col = c("red","darkgreen"),
          main = "两因素析因设计",
          xlab = "时间和方法的交互")
1
2
3
4
5
6
7
8
9
10
11
12
13
14

再介绍一种方法：

library(HH)
## 载入需要的程辑包：lattice
## 载入需要的程辑包：grid
## 载入需要的程辑包：latticeExtra
## 载入需要的程辑包：multcomp
## 载入需要的程辑包：mvtnorm
## 载入需要的程辑包：survival
## 载入需要的程辑包：TH.data
## 载入需要的程辑包：MASS
## 
## 载入程辑包：'TH.data'
## The following object is masked from 'package:MASS':
## 
##     geyser
## 载入需要的程辑包：gridExtra
## 
## 载入程辑包：'HH'
## The following object is masked from 'package:gplots':
## 
##     residplot

interaction2wt(y ~ x1 * x2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

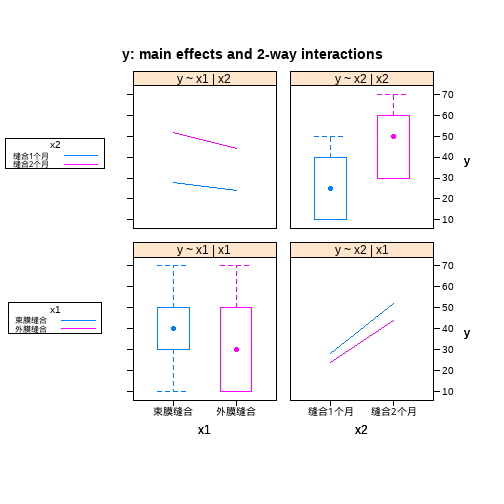
detach(df11_1)
1

I x J 两因素析因设计资料的方差分析

使用课本例11-2的数据，自己手动摘录：

df11_2 <- data.frame(
  druga = rep(c("1mg","2.5mg","5mg"), each = 3),
  drugb = rep(c("5微克","15微克","30微克"),each = 9),
  y = c(105,80,65,75,115,80,85,120,125,115,105,80,125,130,90,65,120,100,75,95,85,135,120,150,180,190,160)
)

str(df11_2)
## 'data.frame':	27 obs. of  3 variables:
##  $ druga: chr  "1mg" "1mg" "1mg" "2.5mg" ...
##  $ drugb: chr  "5微克" "5微克" "5微克" "5微克" ...
##  $ y    : num  105 80 65 75 115 80 85 120 125 115 ...
1
2
3
4
5
6
7
8
9
10
11

数据一共3列，第1列是a药物的剂量（3种剂量，代表3个水平），第2列是b药物的剂量（3种剂量），第3列是镇痛时间。

进行两因素三水平的析因设计资料方差分析：

f2 <- aov(y ~ druga * drugb, data = df11_2)

summary(f2)
##             Df Sum Sq Mean Sq F value  Pr(>F)   
## druga        2   6572    3286   8.470 0.00256 **
## drugb        2   7022    3511   9.050 0.00190 **
## druga:drugb  4   7872    1968   5.073 0.00647 **
## Residuals   18   6983     388                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1
2
3
4
5
6
7
8
9
10

结果和课本也是一模一样的哦！

I x J x K 三因素析因设计资料的方差分析

使用课本例11-3的数据，

df11_3 <- foreign::read.spss("E:/各科资料/医学统计学/研究生课程/析因设计重复测量/8多因素试验ANOVA18-9研/例11-03-5种军装热感觉5-2-2.sav", to.data.frame = T)

df11_3$a <- factor(df11_3$a)

str(df11_3)
## 'data.frame':	100 obs. of  4 variables:
##  $ b: Factor w/ 2 levels "骞茬嚗","娼箍": 1 1 1 1 1 1 1 1 1 1 ...
##  $ c: Factor w/ 2 levels "闈欏潗","娲诲姩": 1 1 1 1 1 1 1 1 1 1 ...
##  $ a: Factor w/ 5 levels "1","2","3","4",..: 1 1 1 1 1 2 2 2 2 2 ...
##  $ x: num  0.25 -0.25 1.25 -0.75 0.4 ...
##  - attr(*, "variable.labels")= Named chr [1:4] "娲诲姩鐜" "娲诲姩鐘舵€\x81" "鍐涜绫诲瀷" "涓昏鐑劅瑙\x89"
##   ..- attr(*, "names")= chr [1:4] "b" "c" "a" "x"
##  - attr(*, "codepage")= int 65001
1
2
3
4
5
6
7
8
9
10
11
12
13

数据一共4列，前3列分别是b因素，c因素，a因素，每个因素有不同的水平，第4列是因变量（展示的图有乱码，不影响使用）。

进行3因素吸引设计资料的方差分析：

f3 <- aov(x ~ b * c * a, data = df11_3)

summary(f3)
##             Df Sum Sq Mean Sq F value   Pr(>F)    
## b            1   9.94    9.94  23.138 6.98e-06 ***
## c            1 283.35  283.35 659.485  < 2e-16 ***
## a            4   5.20    1.30   3.024   0.0224 *  
## b:c          1  12.68   12.68  29.514 5.82e-07 ***
## b:a          4   1.94    0.48   1.128   0.3491    
## c:a          4   1.48    0.37   0.862   0.4905    
## b:c:a        4   1.61    0.40   0.937   0.4472    
## Residuals   80  34.37    0.43                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14

结果也是和课本一模一样。

正交设计资料的方差分析

使用课本例11-4的数据

df11_4 <- data.frame(
  a = rep(c("5度","25度"),each = 4),
  b = rep(c(0.5, 5.0), each = 2),
  c = c(10, 30),
  d = c(6.0, 8.0,8.0,6.0,8.0,6.0,6.0,8.0),
  x = c(86,95,91,94,91,96,83,88)
)

df11_4$a <- factor(df11_4$a)
df11_4$b <- factor(df11_4$b)
df11_4$c <- factor(df11_4$c)
df11_4$d <- factor(df11_4$d)

str(df11_4)
## 'data.frame':	8 obs. of  5 variables:
##  $ a: Factor w/ 2 levels "25度","5度": 2 2 2 2 1 1 1 1
##  $ b: Factor w/ 2 levels "0.5","5": 1 1 2 2 1 1 2 2
##  $ c: Factor w/ 2 levels "10","30": 1 2 1 2 1 2 1 2
##  $ d: Factor w/ 2 levels "6","8": 1 2 2 1 2 1 1 2
##  $ x: num  86 95 91 94 91 96 83 88
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

数据一共5列，前4列是不同的因素，第5列是因变量。

进行正交设计资料的方差分析：

f4 <- aov(x ~ a + b + c + d + a*b, data = df11_4)

summary(f4)
##             Df Sum Sq Mean Sq F value Pr(>F)  
## a            1    8.0     8.0     3.2 0.2155  
## b            1   18.0    18.0     7.2 0.1153  
## c            1   60.5    60.5    24.2 0.0389 *
## d            1    4.5     4.5     1.8 0.3118  
## a:b          1   50.0    50.0    20.0 0.0465 *
## Residuals    2    5.0     2.5                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1
2
3
4
5
6
7
8
9
10
11
12

结果和课本一模一样，用R语言进行方差分析真是太简单了！！！！

本文首发于公众号：医学和生信笔记，完美观看体验请至公众号查看本文。

医学和生信笔记，专注R语言在临床医学中的使用，R语言数据分析和可视化。