自顶向下语法分析（top-down parsing）

输入程序经过词法分析器后产生单词流，并为每个单词流标注了语法范畴。而词法分析器产生的单词流就是语法分析器的输入，语法分析器将为输入的单词流找到推导（或者给不合法的程序输出错误信息），而语法分析树等价于推导，也可以说语法分析器为输入程序构建语法树。基于上下文无关文法的语法分析器主要有两个流派：

• 自顶向下语法分析（top-down parsing）。从根根节点向底部的叶节点方向构造分析树。也可以看作寻找输入串最左推导的过程。
• 自底向上语法分析（bottom-up parsing）。底部的叶节点向顶部的根节点方向构造分析树。

本文将介绍自顶向下语法分析器。从有回溯的自顶向下分析开始介绍，引出无回溯的自顶向下分析，也即 LL(1) 语法分析。

词法分析器和上下文无关文法可以戳下面两篇博客：

正则表达式（RE）、有限自动机（FA）和词法分析（LA）
上下文无关文法（CFG）

有回溯的自顶向下分析：非预测分析法

自顶向下的语法分析器从根开始，向下扩展树，直到树的叶子节点和输入串相匹配。这样的过程其实就是为输入串找推导的过程，很自然给出类似下面的算法：

算法中的 backtrace 是一个回溯的过程，也即为上一个出栈的非终结符选择另一个产生式（右部）压栈。

看一个简单的例子，给定语法 G：
S − > N V T N − > p ∣         t ∣         s V − > e ∣         d T − > g ∣         w ∣         r

SNVT​−>NVT−>p∣       t∣       s−>e∣       d−>g∣       w∣       r​

为输入串 $tdw$ 寻找推导（构建语法树）。使用上述算法迭代过程如下：

也可以采用递归的自顶向下分析算法（递归下降分析）：每一个非终结符编写一个调用过程。

这个朴素的自顶向下的无预测分析算法存在的问题就是回溯，在上述算法过程中，如果每次替换非终结符作出的产生式选择都是糟糕的，那么该算法代价将直线上升。如果可以消除回溯，也就是说语法分析器每次都能选择正确的产生式，那么这个算法将是线性时间的。

无回溯的自顶向下分析：预测分析法

前面介绍的自顶向下语法分析是一个有回溯的语法分析，原因是每次为一个非终结符选择产生式是盲目的，发现不匹配，就需要回溯。在语法分析器选择产生式时，如果可以同时考虑当前关注的符号以及下一个输入符号（称为前瞻符号，lookahead symbol），则可以通过前瞻一个符号，消除选择产生式时的盲目性。这样的自顶向下分析算法就是一个无回溯的算法，也称预测性算法。

无回溯的算法需要构建一张预测分析表，语法分析器前瞻一个符号再查询预测表来选择使用哪个产生式，就可以避免盲目的选择产生式。为了构建这样一张预测表，我们需要先构建 FIRST 集合和 FOLLOW 集合。FIRST 和 FOLLOW 集使得我们可以根据一个输入符，选择应用哪个产生式。

FIRST集和FOLLOW集

$FIRST(\alpha )$ 是指从 $\alpha$ 推导出的字符串开头可能出现的终结符的集合。

例如：
S − > X Y Z X − > a   ∣   b . . .

SX...​−>XYZ−>a ∣ b​

首先，$FIRST(S)=FIRST(XYZ)$。这个时候，计算 $FIRST(S)$，只需要计算 $FIRST(X)$，则 F I R S T ( S ) = { a , b } FIRST(S) = \{ a, b\} FIRST(S)={a,b} ，此时如果输入符号开头是 $b$，则显然选择产生式 $X->b$。但考虑修改上述文法如下：
S − > X Y Z X − > a   ∣   b ∣   ϵ . . .

SX...​−>XYZ−>a ∣ b∣ ϵ​

计算 $FIRST(XYZ)$ 不能只计算 $FIRST(X)$ 了，因为 $X$ 可能产生空串。这个时候就需要考虑能够产生空串的符号，同时还必须考虑跟随在空符号之后的其他符号。这就引入了 FIRST、 NULLABLE 和 FOLLOW 三个集合。

• 如果 X 可以推导出空串，则 $X\in NULLABLE$。
• $FIRST(\alpha )$ 是可以推导出的字符串开头可能出现的终结符的集合。
• $FOLLOW(X)$ 是直接跟随在 $X$ 之后的终结符的集合。例如，存在推导 $Xt$，则 $t\in FOLLOW(X)$。当存在推导 $XYZt$，若 $Y$ 和 $Z$ 都能推导出空串 $ϵ$，则 $t\in FOLLOW(X)$。

我们很容易给出 NULLABLE 归纳定义和相应不动点的算法：

对于下面的文法：
0                  Z − > d 1                     ∣        X Y Z 2                  Y − > c 3                     ∣         ϵ 4                  X − > Y 5                     ∣         a

0                Z1                   2                Y3                   4                X5                   ​−>d∣      XYZ−>c∣       ϵ−>Y∣       a​

很容易得到 N U L L A B L E = { X , Y } NULLABLE=\{ X, Y\} NULLABLE={X,Y} 。

类似的，我们也可以得到 FIRST 集合的归纳定义和不动点算法：

还是上面的例子，计算非终结符号的 FIRST 集：

FOLLOW 集的不动点算法为：

同样计算上述例子的 FOLLOW集：

进一步，可以得到每条产生式的 FIRST_S 集的不动点算法：

这样，我们就可以得到预测分析表

这里的得到预测分析表是有冲突的，也就是说根据前瞻符号查表会得到多个产生式。在后面的章节我们会介绍预测分析表的冲突问题，这里先按下不表。

两种预测分析算法

到这里，如果我们得到无冲突的预测分析表，我们就可以得到无回溯的分析算法了，每次选择产生式的时候，根据前瞻符号查询该表，就可以选择正确的产生式了。到这里，我们就可以得到预测分析算法，一个是递归预测分析算法，一个是非递归预测分析算法（表驱动预测分析）

递归预测分析算法：根据预测分析表为每一个非终结符编写一个调用过程。

非递归预测分析算法：

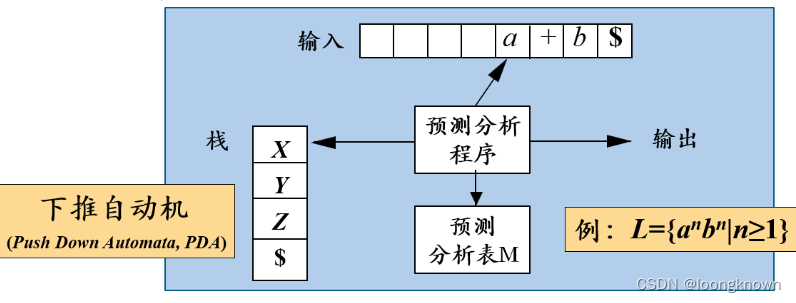
非递归的预测分析器其实就是一个下推自动机（PDA，Push-down Automata）。它一个输入带、一个读头和一个带有预测分析表的控制器构成，与 FA 相比，这个自动机增加了个栈，也叫下推存储器，起到记忆的作用。

LL(1)文法

这个例子的文法产生的预测分析表存在多重定义的项，也即有的表项中存在多个产生式。如果预测分析表不存在多重定义的项，就称其文法为LL(1)文法，对应的预测分析表也称为LL(1)分析表。LL(1)得名于：这种语法分析器由左（Left）到右扫描输入，构建一个最左推导（Leftmost），并且只使用一个前瞻符号（1）。LL(1) 文法是无回溯的文法，使用LL(1)分析表的预测分析算法也就是无回溯的分析算法。

一个文法G是LL(1)的，当前仅当G的任意两个产生式 $A->\alpha |\beta$ 满足下面的条件：

1. 不存在终结符 $a$，使得 $\alpha$ 和 $\beta$ 可以推导出以 $a$ 开头的串。
2. $\alpha$ 和 $\beta$ 只有一个可以推导出空串。
3. 如果 $\beta \stackrel{\ast }{\Rightarrow }ϵ$，那么 $\alpha$ 不能推导出任何以 $FOLLOW(A)$ 中某个终结符开头的串。类似地，如果 $\alpha \stackrel{\ast }{\Rightarrow }ϵ$，那么 $\beta$ 不能推导出任何以 $FOLLOW(A)$ 中某个终结符开头的串。

前两个条件等价于 $FIRST(\alpha )\cap FIRST(\beta )=\varnothing$。第三个条件等价于如果 $ϵ\in FIRST(\beta )$，则 $FIRST(\alpha )\cap FOLLOW(A)=\varnothing$，并且如果 $ϵ$ 在 $FIRST(\alpha )$ 中时类似结论也成立。

这样来看，上一节例子中给的文法显然不是 LL(1) 文法。

文法转换

有的文法不是 LL(1) 文法，可以通过文法转换变成LL(1)文法，常见的转换包括：

• 消除左递归。
• 提取左公因子。

消除左递归

考虑在 CFG 文法中介绍的算术表达式文法的例子，截取部分如下：
E X P R − > E X P R + T E R M ∣         E X P R − T E R M ∣         T E R M T E R M − > T E R M ∗ F A C T O R ∣         T E R M − F A C T O R ∣         F A C T O R

EXPRTERM​−>EXPR+TERM∣       EXPR−TERM∣       TERM−>TERM∗FACTOR∣       TERM−FACTOR∣       FACTOR​

该文法第 1、2、4、5 条产生式左边的终结符和右部第一个符号相同，将导致自顶向下分析器无线循环下去：
E X P R − > E X P R + T E R M − > E X P R + E X P R + T E R M − > E X P R + E X P R + E X P R + T E R M − > E X P R + E X P R + E X P R + E X P R + T E R M − > . . .

EXPR​−>EXPR+TERM−>EXPR+EXPR+TERM−>EXPR+EXPR+EXPR+TERM−>EXPR+EXPR+EXPR+EXPR+TERM−>...​

左递归文法

对一个 CFG 文法，如果其右部的第一个符号与左侧的符号相同或这能够推导出左侧符号，则称该文法为左递归文法。

前一种情况为直接左递归文法，而后一种情况为间接左递归文法。

左递归文法将导致自顶向下分析去无限循环，需要转换其文法以消除左递归。

对于直接左递归文法，消除方法如下：
A − > A α   ∣   β           ⇒            A − >   β A ′ A ′ − >   α A ′   ∣ ϵ

A−>Aα ∣ β         ⇒          AA′​−> βA′−> αA′ ∣ϵ​

则上述算术表达式的左递归可以转换为：
E X P R − > T E R M   E X P R ′ E X P R ′ − > +   T E R M   E X P R ′ ∣        −   T E R M   E X P R ′ ∣        ϵ

EXPREXPR′​−>TERM EXPR′−>+ TERM EXPR′∣      − TERM EXPR′∣      ϵ​

而对于间接左递归，例如下面的文法：
S − > A a   ∣   b A − > A c   ∣   S d   ∣   ϵ

SA​−>Aa ∣ b−>Ac ∣ Sd ∣ ϵ​

由于 $S\Rightarrow Aa\Rightarrow Sda$，因而这是一个简介左递归。

下面的算法可以系统地消除左递归。如果文法中不存在环（即形如 $A\stackrel{+}{\Rightarrow }A$）或 $ϵ$ 产生式（即形如 $A->ϵ$）就能保证消除左递归。算法如下：

使用该算法很容易消除上面例子中的间接左递归。上面的算法，如果有 $ϵ$ 产生式，不保证一定能够得到正确的结果，但也可能得到正确的结果。
S − > A a   ∣   b A − > b d A ′   ∣   A ′ A ′ − > c A ′   ∣   a d A ′   ∣   ϵ

SAA′​−>Aa ∣ b−>bdA′ ∣ A′−>cA′ ∣ adA′ ∣ ϵ​

提取左公因子

同一个非终结符的多个产生式有公共左因子会导致自顶向下分析算法中产生回溯。例如：
A − > α B 1   ∣   α B 2

A​−>αB1​ ∣ αB2​​

对于上面不的文法，开头为 $\alpha$ 的输入串，不知道选择 $\alpha B_1$ 还是 $\alpha B_2$，可以将 $A$ 展开为 $\alpha A^{{}^{\prime }}$，从而推迟决定，等读入足够多的信息后才作出正确的决定。

对上述例子提取左公因子：
A − > α B B − > B 1   ∣   B 2

AB​−>αB−>B1​ ∣ B2​​

些上下文无关语言没有无回溯语法，消除左递归和提取左公因子通常可以消除回溯。但一般来说，对于任意的上下文无关语言，是否存在无回溯语法是不可判定的。

参考：

• Engineering a compiler (2nd Edition)
• Compilers Principles Techniques and Tools (2nd Edition)
• https://mooc.study.163.com/learn/1000002001?tid=1000003000#/learn/content?type=detail&id=1000044013&cid=1000052033