基于马科维茨与蒙特卡洛模型的资产最优配置模型（Matlab代码实现）

  目录

💥1 概述

📚2 运行结果

🎉3 参考文献

👨‍💻4 Matlab代码

---

💥1 概述

资本是保险公司经营的核心要素,是资产配置的重要约束条件。本文在马克维茨方法的基础上,将偿付能力引入了资产配置的优化模型。在使用改进的优化模型后,保险公司的最优投资组合出现变化,而保险公司的偿付能力充足率相应有所改善。本文还对保险公司期初的资本充足度进行了敏感性分析,结果显示,最优投资组合与保险公司的期初资本有相关关系,期初资本充足率越高,保险公司风险资产的占比可以越高。

📚2 运行结果

 

 

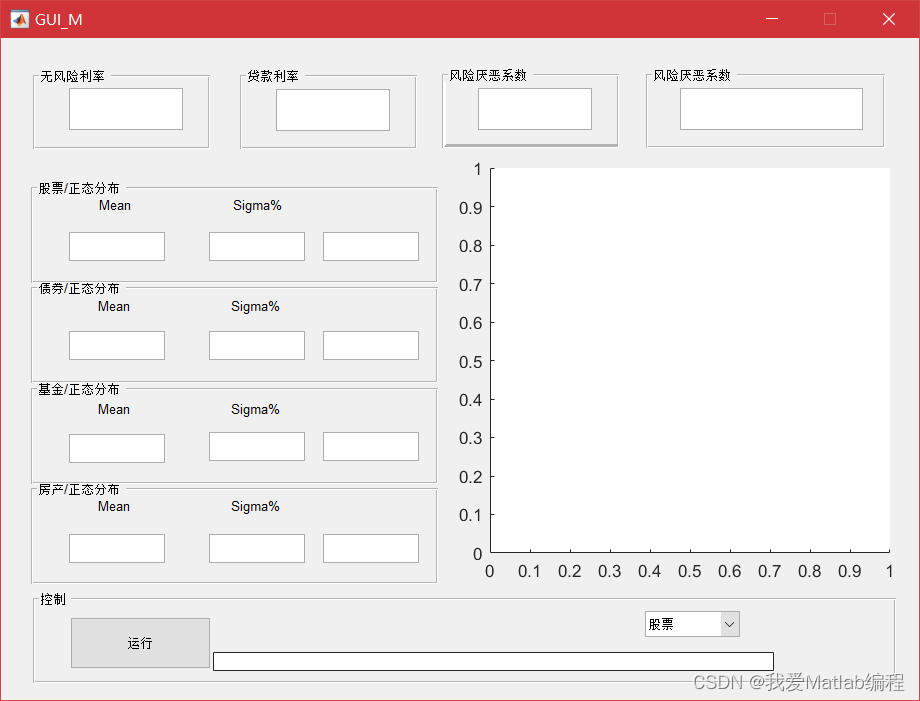
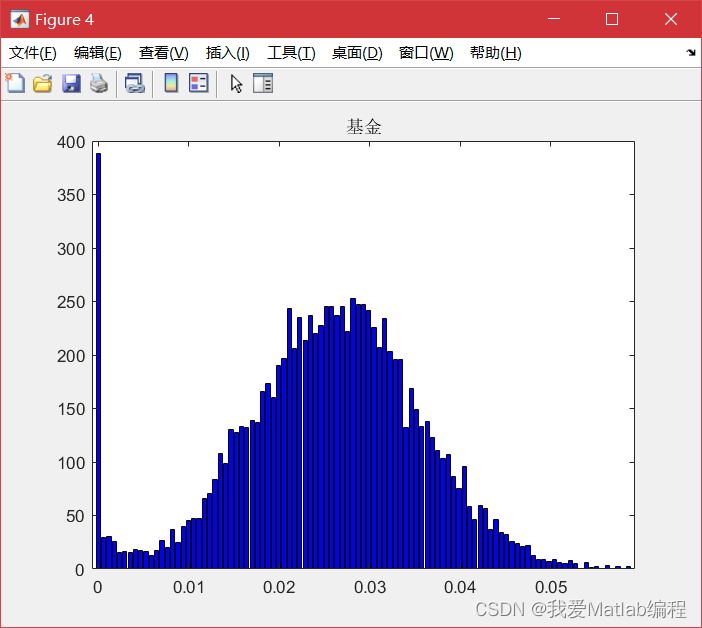
🎉3 参考文献

 [1]卫晓婧,熊立华,万民,刘攀.融合马尔科夫链-蒙特卡洛算法的改进通用似然不确定性估计方法在流域水文模型中的应用[J].水利学报,2009,40(04):464-473+480.

👨‍💻4 Matlab代码

主函数部分代码：

%% 蒙特卡洛仿真模拟无GUI程序代码
clear 
clc
N =10000;%随机模拟的次数
RisklessRate = 0.0306;%无风险利率即银行利率来自9年平均值
BorrowRate   = 0.055;%贷款利率取约定值
RiskAversion = 39.8;%取厌恶系数平均值
%M期望 E为sigma
ExpReturn=[ 11.58    3.87    22.02    0.99 ]./100;
sigma =[0.05 0.01 0.05 0.01];%根据对未来的预期，分别给股票、债券、基金和房产赋予一个sigma
S_M = ExpReturn(1);%股票
S_E = sigma(1);%正态分布标准差
B_M = ExpReturn(2);%债券
B_E = sigma(2);
F_M = ExpReturn(3);%基金
F_E = sigma(3);
H_M = ExpReturn(4);%房产
H_E = sigma(4);
%生成服从正态分布的随机数
S = normrnd(S_M,S_E,N,1);
B = normrnd(B_M,B_E,N,1);
F = normrnd(F_M,F_E,N,1);
H = normrnd(H_M,H_E,N,1);

for i=1:N
    ExpReturns=[S(i) B(i) F(i) H(i)];
%     set(handles.edit13,'string',S(i));
%     set(handles.edit16,'string',B(i));
%     set(handles.edit19,'string',F(i));
%     set(handles.edit22,'string',H(i));
    ExpCovariance=[0.264    -0.01    0.273    0.025
                     -0.01    0.002    -0.013    -0.002
                     0.273    -0.013    0.318    0.028
                     0.025    -0.002    0.028    0.005 ];
            %协方差
    [PortRisk,PortReturn,PortWts]=portopt(ExpReturns,ExpCovariance,20);
    [RiskyRisk,RiskyReturn,RiskyWts,RiskyFraction,OverallRisk,OverallReturn]=portalloc(PortRisk,PortReturn,PortWts,RisklessRate,BorrowRate,RiskAversion);
    RiskWeights=RiskyWts*RiskyFraction
    %show(i,:)=[OverallRisk OverallReturn]
    S1(i) = RiskWeights(1);
    B1(i) = RiskWeights(2);
    F1(i) = RiskWeights(3);
    H1(i) = RiskWeights(4);
    RiskWeights1(i,:)=RiskWeights;
    RiskyWts1(i,:)=RiskyWts;
    RiskyReturn1(i)=RiskyReturn;
    RiskyRisk1(i)=RiskyRisk;
    RiskyFraction1(i)=RiskyFraction;
    OverallRisk1(i) = OverallRisk;
    OverallReturn1(i) = OverallReturn;
end