动态规划：组成目标货币的最少货币数

1、题目

arr 是面值数组，其中的值都是正数且没有重复。再给定一个正数 aim。

每个值都认为是一种面值，且认为张数是无限的。

返回组成 aim 的最少货币数

例如，arr = [2, 5, 10]，

aim = 1000，则最好的方法是用 100 张 10元，返回100。

aim = 1002，100张10元 + 1张2元 = 101，所以返回101。

aim = 104，100张10元 + 2张2元 = 102，所以返回102。

2、思路

从左往右模型，对于 arr 数组中的每个面值，用不超过 aim钱数的张数全试一遍，收集最小张数。

将 arr 排序并不能会更快，比如 arr = [117, 10]，aim = 1000，最优解法是 100 张 10元， 0 张117元。

2.1 暴力递归版本

public class MinCoinsNoLimit {
    public static int minCoins(int[] arr, int aim) {
        return process(arr, 0, aim);
    }
    
    //arr[index...] arr 从index出发往后的所有面值张数自由选择
    // 组成rest这么多钱，返回最小张数
    public static int process(int[] arr, int index, int rest) {
        //rest不可能小于0，因为上游已经控制了
        //if (rest < 0) { //钱数小于0时，认为无穷多张才能组成它，用最大值标记无效解
        //    return Integer.MAX_VALUE;
        //}
        
        if (index == arr.length) {  //没钱了，且rest=0，那么只需要0张组成rest
            return rest == 0 ? 0 : Integer.MAX_VALUE;
        } else {
            int ans = Integer.MAX_VALUE;
            //index位置的面值从0张开始尝试
            for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
                //当前index位置已经做了决定，接下来该index+1位置及其往后的面值做决定
                //剩下的面值搞定剩下的钱的最小张数
                int next = process(arr, index + 1, rest - zhang * arr[index]);
                if (next != Integer.MAX_VALUE) {
                    ans = Math.min(ans, next + zhang);
                }
            }
            return ans;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

2.2 动态规划版本

public class MinCoinsNoLimit {
    public static int minCoins(int[] arr, int aim) {
        if (aim == 0) return 0;
        
        //index: 0~n
        //rest: 0~aim
        int n = arr.length;
        int[][] dp = new int[n + 1][aim + 1];
        dp[n][0] = 0;
        for (int j = 1; j <= aim; j++) {
            dp[n][j] = Integer.MAX_VALUE;
        }
        
        for (int index = n - 1; index >= 0; index--) {
            for (int rest = 0; rest <= aim; rest++) {
                int ans = Integer.MAX_VALUE;
                for (int zhang = 0; zhang * arr[index] <= rest; zhang++) { //枚举行为
                    int next = dp[index + 1][rest - arr[index]];
                    if (next != Integer.MAX_VALUE) {
                        ans = Math.min(ans, next + zhang);
                    }
                }
                dp[index][rest] = ans;
            }
        }
        return dp[0][aim];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

有枚举行为，试着优化。

图中的 a 就是在 当前面值 3 元选择 0 张的时候，剩下的货币凑够 14 元的最小货币数，但是总的货币数还要加上当前 3 元选择的 0 张，其他位置同理。

图中 + 的数字就是当前面值的货币使用的张数，✔️位置的值就是它依赖的所有位置中的最小值。

即：

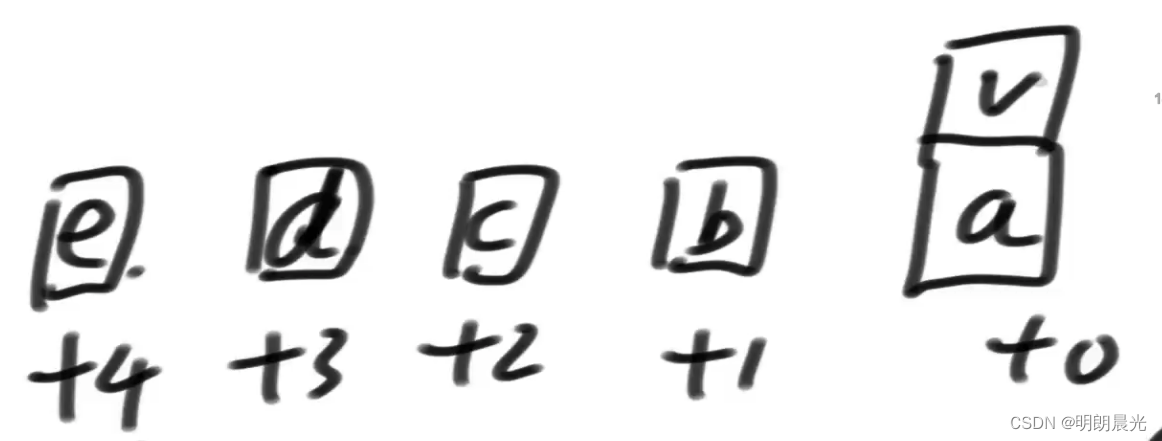
接着观察 ✔️号的左边，而左边这个位置的值是 $b+0，c+1，d+2，e+3$ 的最小值：

而✔️依赖的值是 $b+1，c+2，d+3，e+4$，于是 ✔️ = min { X位置的值 + 1，a}。

所以得到了动态规划的优化版本。

2.3 动态规划优化版本（斜率优化）

public class MinCoinsNoLimit {
    public static int minCoins(int[] arr, int aim) {
        if (aim == 0) return 0;
        
        //index: 0~n
        //rest: 0~aim
        int n = arr.length;
        int[][] dp = new int[n + 1][aim + 1];
        dp[n][0] = 0;
        for (int j = 1; j <= aim; j++) {
            dp[n][j] = Integer.MAX_VALUE;
        }
        
        for (int index = n - 1; index >= 0; index--) {
            for (int rest = 0; rest <= aim; rest++) {
                dp[index][rest] = dp[index + 1][rest]; //上图中的a位置
                //图中x的位置要保证是有效的 且 x的值有效
                if (rest - arr[index] >= 0 && dp[index][rest - arr[index]] != Integer.MAX_VALUE) {
                    dp[index][rest] = Math.min(dp[index][rest], dp[index][rest - arr[index]] + 1);
                }
            }
        }
        return process(arr, 0, aim);
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26