java优先级队列（基于堆）

前言

博主个人社区：开发与算法学习社区

博主个人主页：Killing Vibe的博客

欢迎大家加入，一起交流学习~~

好久没更新数据结构相关的文章了，之前还遗留了优先级队列的文章，现在补上~

一、优先级队列的应用

优先级队列（堆）：按照优先级的大小动态出队（动态指的是元素个数动态变化，而非固定）

普通队列：FIFO按照元素的入队顺序出队，先入先出

现实生活中的优先级队列 PriorityQueue

1.1 医生根据病人排手术排期

排期时包括具体手术时，病人的人数都在动态变化

病情相同的情况下按照先来先排，若病情较重，优先安排手术。

举个栗子：

10.25 安排手术 10.26 手术 手术三人

此时若突然来了一个病情比较严重的病人，优先安排手术。

此时数据在动态变化

和排序的区别：

排序指的是当前集合的元素个数是确定的，不会发生变化。

1.2 操作系统的任务调度

系统的任务一般都比普通的应用要高

CPU、内存等资源是有限的，当资源不够用时，优先让优先级较高的应用获取资源

二、基于二叉树的堆（二叉堆）

2.1 二叉堆的特点

2.1.1 二叉堆的存储结构

二叉堆是一颗完全二叉树，基于数组存储（元素都是靠左排列，数组中存储时不会浪费空间）

只有完全二叉树适合使用数组这种结构来存储, 其他的二叉树都要用链式结构

2.1.2 关于节点值

堆中根节点值 >= 子树节点中的值（最大堆，大根堆）

堆中根节点值 <=子树中节点的值（最小堆，小根堆）

节点的层次和节点的大小没有任何关系，只能保证当前树中，树根是最大值。其他节点层次大小关系不确定。

堆中树根 >= 子树中所有节点，所有子树也仍然满足堆的定义。

注意：

1. JDK中的PriorityQueue默认是基于最小堆的实现。

2. 最大堆中“高”的结点未必就比 “低”的结点大（如上图）

2.1.3 二叉堆的父子结点编号

因为堆是基于数组来存储的，节点的之间的关系通过数组下标表示

从0开始编号，数组下标也是从0开始

假设此时结点编号为 i ，且存在父节点

• 父节点编号 parent = （i -1）/2

• 左子树的编号 left = 2 * i +1

• 右子树的编号 right = 2 * i +2

2.2 二叉堆的基础表示

2.2.1 向堆中添加元素（shiftUp操作）

从尾部新增一个元素52，堆是数组实现的。

此时这个堆仍然满足完全二叉树的性质。

但是此时这个完全二叉树就不再是一个最大堆了，因此需要进行元素的上浮操作，让新添加的元素上浮到合适位置。

步骤如下：

1.尾部添加新元素

2. 不断将此时索引 k 和父节点的索引 i 对应的元素进行大小关系比较，若大于父节点就交换彼此的节点值，直到当前节点 <= 父节点为止 or 走到树根。

交换

最后52上浮到最大的位置

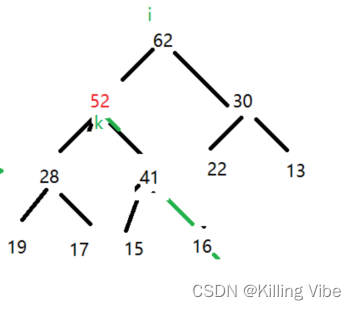
上浮操作的终止条件：

1. 当前已经上浮到树根 =》 这个元素一定是最大值
2. 当前元素 <= 父节点对应的元素值，此时元素落到在正确位置

2.2.2 在堆中取出最大值（shiftDown 操作）

在堆顶取得最大值后，如何移动元素可以保证此时还是个最大堆呢？

步骤如下：

1. 最大堆的最大值一定处在树根节点，直接取出树根即可
2. 需要融合左右两个子树，使得取出树根后这棵树仍然是最大堆
3. 将堆中最后一个元素顶到堆顶，然后进行元素的下沉操作。 shifDown后 使其仍然满足最大堆的性质

其实堆排序就是建立最大堆，然后在最大堆的基础上进行调整操作，就可以得到一个升序集合~~

2.2.3 堆化（heapify）

现在给一个任意的整型数组 =》 都可以看作是一个完全二叉树，距离最大堆就差元素调整操作。

方法一：建堆

将这n个元素依次调用add方法添加到一个新的最大堆中，遍历原数组，创建一个新的最大堆，调用最大堆的add方法即可。

时间复杂度为：O($nlogn$)

空间复杂度为：O($n$)

方法二：原地heapify（重要）

从最后一个非叶子结点开始进行元素siftDown操作

从当前二叉树中最后一个小子树开始调整，不断向前，直到调整到根节点。

不断将子树调整为最大堆的时，最终走到树根时，左右子树已经全部是最大堆，只需最后下沉根节点就能的到最终的最大堆。

时间复杂度为 Sn = $nlo{g}_2(n+1)$ ，因此最终可得渐进复杂度为O($n$）

三、代码实现

写一个基于动态数组实现最大堆的实例：

import java.util.ArrayList;
import java.util.List;
import java.util.NoSuchElementException;

public class MaxHeap {
    // 实际存储元素的数组
    private List<Integer> elementData;
    // 当前堆中元素个数
    private int size;

    public MaxHeap() {
        this(10);
    }

    public MaxHeap(int size) {
        elementData = new ArrayList<>(size);
    }

    /**
     * 将任意的整型数组arr调整为堆
     * @param arr
     */
    public MaxHeap(int[] arr) {
        elementData = new ArrayList<>(arr.length);
        // 1.先将所有元素复制到data数组中
        for (int i : arr) {
            elementData.add(i);
            size ++;
        }
        // 2.从最后一个非叶子结点开始进行siftDown操作
        for (int i = parent(size - 1); i >= 0; i--) {
            siftDown(i);
        }
    }

    public void add(int val) {
        // 1.直接向数组末尾添加元素
        elementData.add(val);
        size ++;
        // 2.进行元素的上浮操作
        siftUp(size - 1);
    }

    /**
     * 取出当前最大堆的最大值
     * @return
     */
    public int extractMax() {
        if (size == 0) {
            throw new NoSuchElementException("heap is empty!cannot extract!");
        }
        // 树根就是最大值结点
        int max = elementData.get(0);
        // 将数组的末尾元素顶到堆顶
        elementData.set(0,elementData.get(size - 1));
        // 将数组的最后一个元素从堆中删除
        elementData.remove(size - 1);
        size --;
        // 进行元素的下沉操作，从索引为0开始
        siftDown(0);
        return max;
    }

    public int peekMax() {
        if (isEmpty()) {
            throw new NoSuchElementException("heap is empty!cannot peek!");
        }
        return elementData.get(0);
    }

    /**
     * 从索引k开始进行元素的下沉操作
     * @param k
     */
    private void siftDown(int k) {
        // 还存在子树
        while (leftChild(k) < size) {
            int j = leftChild(k);
            // 此时还存在右子树
            if (j + 1 < size && elementData.get(j + 1) > elementData.get(j)) {
                // 此时还存在右子树且右子树的值还比左子树大
                j ++;
            }
            // 索引j一定对应了左右子树的最大值索引
            if(elementData .get(k) >= elementData.get(j)) {
                // 当前元素 >= 左右子树最大值，下沉结束，元素k落在了最终位置
                break;
            }else {
                swap(k,j);
                k = j;
            }
        }
    }


    private void siftUp(int k) {
        while (k > 0 && elementData.get(k) > elementData.get(parent(k))) {
            swap(k,parent(k));
            k = parent(k);
        }
    }

    private void swap(int k, int parent) {
        int child = elementData.get(k);
        int parentVal = elementData.get(parent);
        elementData.set(k,parentVal);
        elementData.set(parent,child);
    }


    public int getSize() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    /**
     * 找到结点k对应的父节点的索引
     * @param k
     * @return
     */
    private int parent(int k) {
        return (k - 1) >> 1;
    }

    /**
     * 找到结点k对应的左子树的索引
     * @param k
     * @return
     */
    private int leftChild(int k) {
        return (k << 1) + 1;
    }

    /**
     * 找到结点k对应的右子树的索引
     * @param k
     * @return
     */
    private int rightChild(int k) {
        return (k << 1) + 2;
    }

    @Override
    public String toString() {
        return elementData.toString();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151

总结

基于堆的优先级队列可以用于解决Top K问题，博主推荐几道💪扣编程题：

• 面试题17.14 最小K个数
• 347.前k个高频元素
• 373.查找最小的K对数字

后续博主会更新自己的题解以及思路，大家也可以自己做做，看看官方题解~