计算机视觉算法——基于Anchor Free的目标检测网络总结

计算机视觉算法——基于Anchor Free的目标检测网络总结

在之前我有总结过一些目标检测网络：
计算机视觉算法——目标检测网络总结
这些方法大都是Anchor Based方法，Anchor Based方法的主要问题是：

1. 检测器的性能和Anchor的Size和Aspect Ratio相关，在RetinaNet中改变Anchor能造成4%的AP的变化；
2. 一般Anchor的Size和Aspect Ratio是固定的，很难处理形状变化大的目标，当发生任务迁移时，往往需要重新设计Anchor；
3. 为了达到召回率，一般需要在图片中生成非常密集的Anchor Boxes。在训练时绝大部分的Anchor Boxes都会时负样本，容易造成正负样本不均的情况。
4. Anchor的引入会使得网络的训练过程变得更加繁琐，想了解这一点大家可以去看看SSD的源码。

1. CornerNet

CornerNet发表于2018年ECCV，原论文名为《CornerNet: Detecting Objects as Paired Keypoints》，该论文将目标检测问题当作关键点检测问题来解决，通过检测目标框的左上角和右下角两个关键点得到预测框。从同期SOTA方法在MS COCO数据集的对比i结果看，相对于One-Stage方法精度有明显提升，但是相对于Two-Stage方法精度接近，但是该方法在推断时间上无优势：

1.1 关键知识点——网络结构及特点

网络结构如下图所示：

如上图所示，ConerNet模型包括三部分，首先是通过堆叠两个Hourglass Network提取图像Feature，然后就是将图像Feature分别通过Top-left Corner和Bottom-right Corner两个Prediction Modules。

Prediction Module的具体结构如下图所示：

可以看出来Prediction Module整体是一个残差结构，其中Top-Left Corner Pooling Module我们稍后介绍，这里先看下Prediction Module的输出包括三部分：Heatmaps，Embeddings，Offsets。

1. Heatmaps用于预测角点的位置，输出的是$C$个Channel的Feature，$C$指的是分类的类别个数（不包括背景类别）
2. Embeddings用于对Corner进行分组，Heatmap上检测个角点如何判断是否属于同一个物体呢？就是通过Embeddings输出之间的距离来找到角点之间的对应关系，我看源码这里Embedings输出的是Channel数为1的Feature。
3. Offsets用于对预测角点位置进行精修。输出的是Channel数为2的Feature，如下公式所示：$${\mathbf{o}}_k=\left(\frac{x_k}{n}-\lfloor \frac{x_k}{n}\rfloor ,\frac{y_k}{n}-\lfloor \frac{y_k}{n}\rfloor \right)$$我们通过Heatmaps输出的位置还原到原始分辨率后肯定是一个取整后的位置$\left(\lfloor \frac{x}{n}\rfloor ,\lfloor \frac{y}{n}\rfloor \right)$，为了恢复原始分辨率的精度，网络就会输出这样一个修正量${\mathbf{o}}_k$

此外，在上图中还有一个Top-left Corner Pooling Module操作，该操作公式如下：
t i j = { max ⁡ ( f t i j , t ( i + 1 ) j )  if  i < H f t H j  otherwise  t_{i j}=\left\{

\right. tij​={max(ftij​​,t(i+1)j​)ftHj​​​ if i<H otherwise ​ l i j = { max ⁡ ( f l i j , l i ( j + 1 ) )  if  j < W f l i W  otherwise  l_{i j}=\left\{

max(flij,li(j+1)) if j<WfliW otherwise " role="presentation">max(flij,li(j+1))fliW if j<W otherwise $$\begin{array}{cc}max\left(f_{l_{ij}},l_{i(j+1)}\right)& \text{ if }j<W\\ f_{l_{iW}}& \text{ otherwise }\end{array}$$

\right. lij​={max(flij​​,li(j+1)​)fliW​​​ if j<W otherwise ​其实就是取水平和竖直最大值，最后求和，具体的案例下图所示：

论文认为Corner Pooling之所以有效，是因为（1）目标定位框的中心难以确定，和边界框的四条边相关，但是每个顶点只与边界框的两条边相关，所以Corner跟他容易获取；（2）顶点更有效提供离散边界空间，作者做了Corner Pooling的实验如下：

1.2 关键知识点——正负样本匹配

对于每个角点，只有一个正样本，其余的都是负样本。但是为了保证样本均衡，作者在角点半径范围内区域会加大对负样本的惩罚力度。实际怎么做呢？

在构建Heatmaps Groundtruth时，如果不加任何惩罚，那么正样本处应该就为1，而负样本处为0；而加上惩罚后就是在角点半径范围内构建一个$e^{-\frac{x^2+y^2}{2{\sigma }^2}}$的高斯分布，该$\sigma$可以是个固定值，可以与物体大小相关，总而言之是越靠近角点的地方越接近于1，越远离角点的地方越接近于0。如下图所示：

作者做了负样本惩罚的消融实验如下：
注意，这里还是只有角点一个正样本，在计算$L_{\text{pull }}$、$L_{\text{push }}$和$L_{off}$时还是只在角点处计算。

1.3 关键知识点——损失计算

Corner损失函数定义如下：$$L=L_{\text{det }}+\alpha L_{\text{pull }}+\beta L_{\text{push }}+\gamma L_{off}$$其中
$L_{\text{det }}$是Heatmaps的Loss，采用的是Focal Loss，准确地说，是针对Heatmaps改进的Focal Loss，公式如下所示： L det  = − 1 N ∑ c = 1 C ∑ i = 1 H ∑ j = 1 W { ( 1 − p c i j ) α log ⁡ ( p c i j )  if  y c i j = 1 ( 1 − y c i j ) β ( p c i j ) α log ⁡ ( 1 − p c i j )  otherwise  L_{\text {det }}=\frac{-1}{N} \sum_{c=1}^C \sum_{i=1}^H \sum_{j=1}^W\left\{

\right. Ldet ​=N−1​c=1∑C​i=1∑H​j=1∑W​{(1−pcij​)αlog(pcij​)(1−ycij​)β(pcij​)αlog(1−pcij​)​ if ycij​=1 otherwise ​其中$y_{cij}$为真值，$p_{cij}$是预测值，我们分两部分来解释该公式：

1. 当$y_{cij}=1$时，此时如果$p_{cij}$接近于1时，说明该真值是容易预测的，那么我们减少其在样本中的权重，所以在log损失的基础上乘以${\left(1-p_{cij}\right)}^{\alpha }$；反之，如果$p_{cij}$接近于0，说明该角点还没有学习到，所以会加大其权重。
2. 而$y_{cij}$不为$1$时，$p_{cij}$应该输出$0$。在角点附近$p_{cij}$输出接近于1的概率时容易造成误检，为了对角点附接近于1的${\left(p_{cij}\right)}^{\alpha }$进行抑制，因此在log损失上乘以${\left(p_{cij}\right)}^{\alpha }$，这样网络就会更加关注这些误检的点，但是又正由于这个已经接近于角点了，因此输出稍微大一些也是情有可原的，因此用${\left(1-y_{cij}\right)}^{\beta }$来抑制一下惩罚。当然，如果在距离角点较远的地方输出接近于$1$肯定也是不对的，那么此时${\left(1-y_{cij}\right)}^{\beta }$和${\left(p_{cij}\right)}^{\alpha }$都会用来加强惩罚。反之，如果$p_{cij}$接近于0，那么${\left(p_{cij}\right)}^{\alpha }$就会告诉网络，这个负样本已经学好了，不需要太多关注。

$L_{\text{pull }}$和$L_{\text{push }}$是Embeddings的Loss，$L_{\text{pull }}$使同一函目标的顶点进行分组，$L_{\text{push }}$用与分离不同目标的顶点：$$L_{\text{pull }}=\frac{1}{N}\sum _{k=1}^N\left[{\left(e_{t_k}-e_k\right)}^2+{\left(e_{b_k}-e_k\right)}^2\right]$$$$L_{push}=\frac{1}{N(N-1)}\sum _{k=1}^N\sum _{\begin{array}{c}j=1\\ j\ne k\end{array}}^N\max \left(0,\Delta -\left|e_k-e_j\right|\right)$$其中$e_k$为真值，其他为网络输出结果，$\Delta$为在作者实验中设置为1，我们简单分析下就可以看出，同一物体的$L_{\text{pull }}$应该为$0$，而不同物体的Embeddings结果如果比较越接近$L_{push}$就会越大。
$L_{off}$是Offsets的Loss，采用的是Smooth L1 Loss，公式如下：$$L_{off}=\frac{1}{N}\sum _{k=1}^{N}SmoothL1Loss\left({\mathbf{o}}_k,{\hat{\mathbf{o}}}_k\right)$$$L_{\text{det }}$在正负样本处都会计算，而$L_{\text{pull }}$、$L_{\text{push }}$和$L_{off}$只在正样本处计算

2. CenterNet

CenterNet发表于2019年，原论文名为《Objects as Points》，CenterNet感觉是基于CornerNet进行的该井，使得检测速度和精度相比于One-Stage和Two-Stage的方法都了不小的提高，在和YOLO v3的比较中，相同速度下，CenterNet提高了4个左右的点。同时网络经过少量的扩展，就可以迁移到3D目标检测和人体关键点检测上。

2.1 关键知识点——网络结构及特点

CenterNet的网络结构是非常简单的，其实就是一个Backbone加上3个Head，3个Head分别输出80维的类别、2维的中心点坐标和2维的长宽偏置。Backbone的示意图如下图所示：

从左到右分别是（a）Hourglass-104，（b）ResNet，（c）DLA-34，（4）Modified DLA-34，CornerNet的Head是从1/4下采样率的Feature上接出来的，作者在论文中对比了不同的BackBone的结果，如下图所示，其中Hourglass效果是最好的：

2.2 关键知识点——损失计算

CornreNet的损失由三部分构成，分别是类别损失、目标中心偏置损失和目标大小损失：$$L_{\text{det }}=L_k+{\lambda }_{\text{size }}{L}_{\text{size }}+{\lambda }_{\text{off }}{L}_{off}$$首先，类被采用的是类别损失采用的Focal Loss:
L k = − 1 N ∑ x y c { ( 1 − Y ^ x y c ) α log ⁡ ( Y ^ x y c )  if  Y x y c = 1 ( 1 − Y x y c ) β ( Y ^ x y c ) α log ⁡ ( 1 − Y ^ x y c )  otherwise  L_k=\frac{-1}{N} \sum_{x y c}\left\{

\right. Lk​=N−1​xyc∑​⎩ ⎨ ⎧​(1−Y^xyc​)αlog(Y^xyc​)(1−Yxyc​)β(Y^xyc​)αlog(1−Y^xyc​)​ if Yxyc​=1 otherwise ​该公式的和CornerNet中的公式没有区别，在此就不再赘述。
目标中心偏置损失采用的是L1 Loss，如下所示：$$L_{off}=\frac{1}{N}\sum _p\left|{\hat{O}}_{\tilde{p}}-\left(\frac{p}{R}-\tilde{p}\right)\right|$$其中，$\hat{O}\in {\mathcal{R}}^{\frac{W}{R}\times \frac{H}{R}\times 2}$为网络输出，$R$是特征图下采样倍率，$p$为原始图像中心点坐标，$\tilde{p}$为特征图上中心点坐标。
目标大小损失使用的同样是L1损失：$$L_{size}=\frac{1}{N}\sum _{k=1}^N\left|\hat{S}{p}_k-s_k\right|$$其中$\hat{S}\in {\mathcal{R}}^{\frac{W^{\prime }}{R}\times \frac{H}{R}\times 2}$为预测值，$s_k=\left(x_2^{(k)}-x_1^{(k)},y_2^{(k)}-y_1^{(k)}\right)$为真值，$\left(x_1^{(k)},y_1^{(k)},x_2^{(k)},y_2^{(k)}\right)$分别为左上角和右下角坐标。

3. FCOS

FCOS发表于2019年CVPR，原论文名为《Fully Convolutional One-Stage Object Detection》，它与当时的SOTA方法结果对比如下：

3.1 关键知识点——网络结构及特点

网络结构如下图所示：

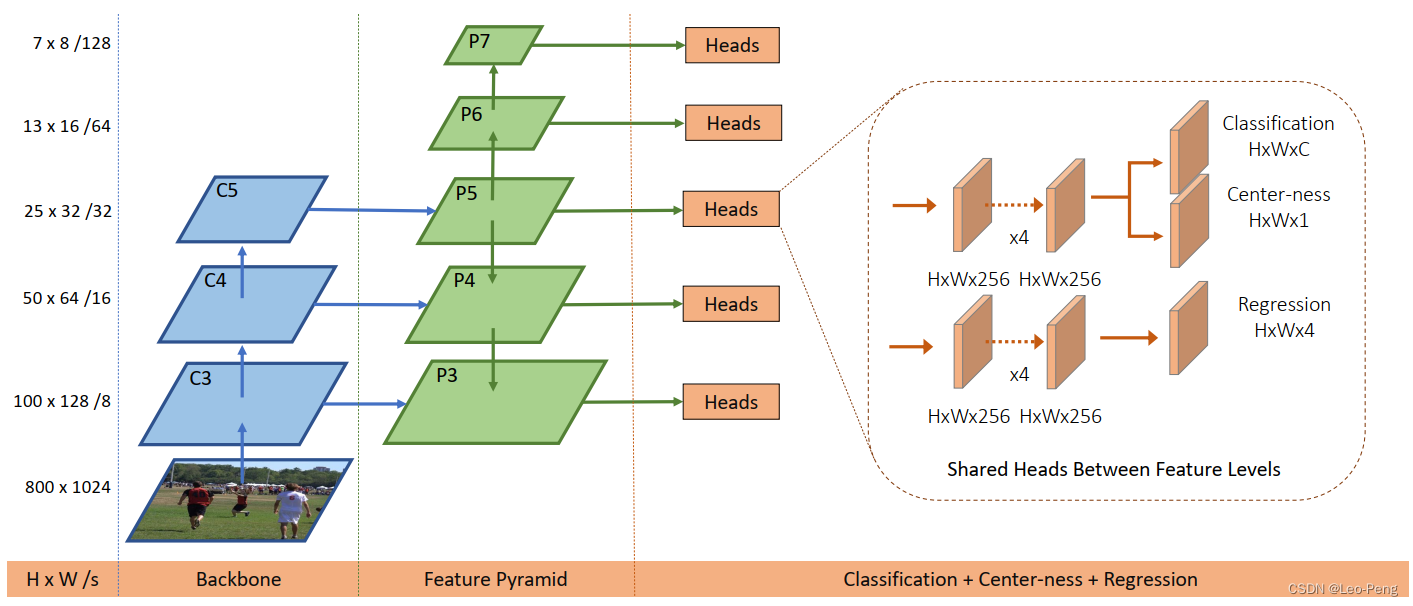
通过上图网络结构还是一目了然的，需要注意的几点是：

1. 不同分辨率上的检测头是共享权重的，每个头都是先经过四个Conv+Group Nomalization+ReLU的模块，最后通过Kernel Size为3的卷积输出。
2. Classification头一共有80个Channel，对应COCO数据集的80个类别，也就是说每一个Grid对应的就只有一个类别输出。
3. Regression头输出的是四个值，分别是距离边框左侧、上侧、右侧、底侧的距离：$$x_{\min }=c_x-l\cdot s$$$$x_{\min }=c_x-t\cdot s$$$$x_{\min }=c_x-r\cdot s$$$$x_{\min }=c_x-b\cdot s$$其中$l,t,r,b$为网络的输出值，由于输出值是在特征图的尺度上，因此需要乘以一个尺度参数$s$。$c_x,c_y$是参考点映射到原图的坐标。
4. Centerness头输出的是一个值，反应的是预测点相对与目标中心点的远近程度：$$\text{ centerness }=\sqrt{\frac{\min \left(l^{\ast },r^{\ast }\right)}{\max \left(l^{\ast },r^{\ast }\right)}\times \frac{\min \left(t^{\ast },b^{\ast }\right)}{\max \left(t^{\ast },b^{\ast }\right)}}$$其中$l^{\ast },t^{\ast },r^{\ast },b^{\ast }$是当前预测点相对于Ground Truth各个方向边界的距离，该值输出的范围是0-1，当预测点位于Ground Truth的Bounding Box的中心点时，该值为1，当位于Bounding Box的边界时，该值为0。在论文中，作者有做关于Centerness头的消融实验
   
   我们可以看到，当加入Centerness监督时，AP都有非常大的提升。

3.2 关键知识点——正负样本匹配

关于FCOS的正负样本匹配一共有两个版本，最开始的版本作者将落入Ground Truth的Bounding Box内的Grid都作为正样本，但是后来通过是实验发现，落入Ground Truth的Bounding Box的中心部分区域的Grid的作为正样本。

由于我们每个Grid只会输出一种类别，如果同一个Grid同时落入两个Ground Truth Bounding Box中，就会面临一个Ambiguity问题，在论文中，作者指出这种情况就会默认将该Grid分配面积Area最小的Ground Truth Box。如下图就会分配给球拍：

但是结合FPN结构，将不同大小的GroundTruth分配到不同分辨率输出上，该问题可以得到大大缓解。

3.3 关键知识点——损失计算

FCOS的损失计算函数如下： L ( { p x , y } , { t x , y } ) = 1 N pos  ∑ x , y L c l s ( p x , y , c x , y ∗ ) + λ N p o s ∑ x , y 1 { c x , y ∗ > 0 } L r e g ( t x , y , t x , y ∗ ) + λ N p o s ∑ x , y 1 { c x , y ∗ > 0 } L c e n t e r n e s s ( s x , y , s x , y ∗ )

L({px,y​},{tx,y​})​=Npos ​1​x,y∑​Lcls​(px,y​,cx,y∗​)+Npos​λ​x,y∑​1{cx,y∗​>0}​Lreg​(tx,y​,tx,y∗​)+Npos​λ​x,y∑​1{cx,y∗​>0}​Lcenterness​(sx,y​,sx,y∗​)​其中分类损失$L_{\mathrm{cls}}$采用的BECLoss+FocalLoss，回归损失$L_{\mathrm{reg}}$和中心度损失$L_{\mathrm{centerness}}$损失只计算正样本下的损失。回归损失$L_{\mathrm{reg}}$为GIoULoss，而$L_{\mathrm{centerness}}$损失为BCELoss。

4. YOLOX

YOLOX发表于2021年，原论文名为《YOLOX: Exceeding YOLO Series in 2021》，YOLOX相对于之前的YOLO版本的一些的亮点在于：Anchor-Free，Decoupeld Detection Head和Advanced Label Assigning Strategy。与SOTA方法对比如下，相对于YOLO v5是有一定的提升：

4.1 关键知识点——网络结构及特点

YOLOX的Backbone的和YOLO v5的Backbone是一摸一样的，对YOLO v5 BackBone不熟悉的同学可以参考计算机视觉算法——目标检测网络总结，该Backbone主要的特点是使用CSP-Darknet53、SPPF和CSP-PAN的模块或者结构。

YOLOX采用的Decoupled Head，这与YOLO v5的Coupled Head的区别如下图所示：

其中Coupled Head和Decoupled Head具体区别是：

1. Coupled Head通过一个$1\times 1$的卷积最后输出维度为$N\times (C+4+1)$的预测结果，并且不同分辨率的检测头参数共享。而Decouple Head是分别通过三个ConvBNSiLU模块和$1\times 1$的卷积后分别输出$C,4,1$的预测结果，分别对应类别、位置参数和IoU，其中IoU具体指的在训练过程中是如果该某样本被划分为正样本时，那么IoU的GroundTruth为1，而如果该Head预测为负样本时，那么IoU的GroundTruth为0。
2. 在Coupled Head中不同分辨率下的参数共享，而Decouple Head在不同分辨率下参数不共享。
3. Coupled Head中预测的四个位置信息是和对应的Anchor强相关的，而Decoupled Head中使用的Anchor Free的思想，其预测的位置信息计算公式如下所示：$$x_{\text{center }}=c_x+t_x$$$$y_{\text{center }}=c_y+t_y$$$$w=e^{t_w}$$$$h=e^{t_h}$$其中$t_x,t_y,t_w,t_h$为网络输出参数，$c_x,c_y$对应栅格的左上角坐标

论文中指出使用Decoupled head不但使得收敛速度变快，同时使得AP也有所提升：

4.2 关键知识点——正负样本匹配

YOLOX中使用的正负样本匹配的是SimOTA，SimOTA是OTA（Optimal Transport Assignment）简化得到的，OTA对应的论文名为《Optimal transport assignment for object detection》，目的是将匹配正负样本的过程看成一个最优传输问题，和DETR中的匹配方法区别是，在DETR中预测结果和真值是一对一匹配，而在SimOTA中预测结果和真值是多对一匹配。下面我们来具体看下：

首先为什么要左SimOTA呢，主要是为不同的目标设定不同数量的正样本数，假如我们在一张图中同时检测一个人和一个网球，如果在人和网球设置相同多的正样本，因为人和网球的大小有着明显的区别，因此要么人就只有一两个正样本，要么网球就会很多低质量的正样本，这样肯定是不合理的。在FCOS中，将正样本数量和真值Bounding Box的大小关联在一定程度上解决了该问题，而SimOTA则是将这一解决方案做得更加细致了。

SimOTA步骤如下：

1. 确定正样本候选区域;
2. 计算每个正样本对Ground Truth的Regression Loss和Class Loss作为匹配的Cost;
3. 获取每个Ground Truth分配到的正样本数，具体操作是计算IOU大小前10的的样本，将前10样本的IOU相加取整则得到Dynamic_K，即Ground Truth应该分配到的正样本数。
4. 为每个Ground Truth取Cost最小的前Dynamic_K个样本作为正样本。
5. 人工去掉同一个样本被分配到多个Ground Truth的正样本的情况。

这里我们来理解下第3步中的Dynamic_K的原理，其实很好理解，还是以人和网球的例子为例，同样分辨率的特征图上，与人的Ground Truth IOU较大的预测值肯定较多，因此按照第3步计算出来的Dynamic_K肯定就大，人获得的正样本就多。

如下表所示，SimOTA给网络带来了2.3个点的AP提升：

4.3 关键知识点——损失计算

由于在网络检测头中有类别、位置参数和IoU三个分支，因此损失由$L_{cls}、L_{reg}、L_{iou}$这三部分组成：$$Loss=\frac{L_{cls}+\lambda L_{reg}+L_{iou}}{N_{pos}}$$其中$L_{cls}、L_{iou}$由BCELoss，而$L_{reg}$采用的是IoULoss，还需要注意的是，$L_{cls}、L_{reg}$只计算正样本损失，而$L_{iou}$既计算正样本损失有计算负样本损失，其实可以理解为我们先判断这里是否存在物体，然后再看物体的类别和位置。$N_{pos}$指的是被划分为正样本的Anchor Point数。

以上就是我对几篇Anchor Free的方法的总结，有问题欢迎交流~